| 1章 式の計算 式の展開式の乗法・除法 因数分解 式の計算の利用 |
4章 二次関数 関数とグラフ 関数の利用 |
|
2章 平方根 平方根 |
5章 図形と相似 相似,三角形の相似 平行線と線分,面積,体積比 相似の利用 (円周角) |
| 3章 二次方程式 2次方程式の解法 (解の公式) 2次方程式の利用 |
6章 三平方の定理 三平方の定理 三平方の定理の利用 |
| 2⃣ 次の2次方程式を解きなさい。 (2) 4x²-49=0 (3) (x+1)²=36 (4) 3(x-3)²=9 |
| 2⃣ 次の2次方程式を解きなさい。 (5) x²+7x+12=0 (7) x²+x-30=0 (8) x²-6x+5=0 (10) (x-3)(x+9)=3(2x+3) |
| 4⃣-1 次の問いに答えなさい。 (1) 次の方程式を解きなさい。 (x-3)²-5(x-3)-14=0 |
| (2) xの2次方程式 2x²+ax-6=0の解の1つが-3のとき、 aの値を求めなさい。また、もうひとつの解を求めなさい。 |
| 4⃣-2 次の問いに答えなさい。 (3) xの2次方程式 2x²+mx-m²=0の解の1つが1のとき、 定数mの値を求めなさい (4) xの2次方程式 x²+ax+b=0が-2と8を解にもつとき、 定数a,bの値を求めなさい。 |
| 5⃣ (1) 連続する3つの正の整数がある。最も小さい数と最も大きい数の積は、 中央の数の3倍より39大きい。これら3つの整数を求めなさい。 |
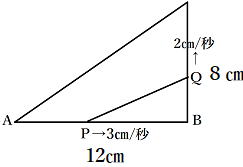
| 5⃣ (2) 右の図のような△ABCで,点Pは辺AB上を 毎秒3㎝の速さでAからBまで動く。 また、点Qは点Pが出発するのと同時にBを 出発し、辺BC上を毎秒2㎝の速さでBからC まで動く。 △PBQの面積が△ABCの面積の 1/8(8分の1)になるのは、点Pが点Aを出発 してから何秒後ですか。 |
 |
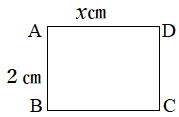
| 5⃣ (3) 右の図のような,AB=2㎝,AD=x㎝の 長方形ABCDがある。この長方形を,ABを 軸として1回転させてできる立体の表面積 は96π㎠だった。このとき,辺ADの長さを 求めなさい。 |
 |
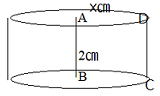
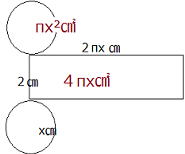
| 5⃣の(3) 解説と解答 ABを軸として回転させると右上図のようになります。 円柱の表面積は右下図から(2×2πx)に円の面積(πx²)を2つ足しますので2πx²。 4πx+2πx²=96π (右図参照) 式を整理して 2x+x²=48 x²+2x-48=0 (x+8)(x-6)=0 x=-8,6 x=-8は問いにあわない。 よってx=6 AD=6㎝ |
  |
| 7⃣ (1) yはxの2乗に比例し,x =3のとき y=27です。 yをxの式で表しなさい。 |
| 7⃣ (2) yはxの2乗に比例し,x =-2のとき y=-1 です。 x=3のときのyの値を求めなさい。 |
7⃣の(2) 解答
yはxの2乗に比例するので、まずy=ax2 と置きましょう。
-1=4a a=-![]() よって y=-
よって y=-![]() x2
x2
よってx=3のときのyの値は -![]() …答
…答
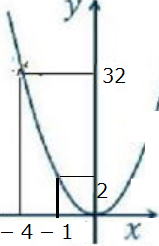
| 7⃣ (5) y=2x²について,x の変域-4≦x≦-1 のとき、 yの変域を求めなさい。 |
| 7⃣の(5) 解説と答 まず、簡単な図を書こう。 xの変域-4≦x≦-1だから 図から 2 ≦y≦ 32 …答 |
 |
| 7⃣ (6) y=-x²について,x の値が-5から-1 まで増加するときの変化の割合を求めなさい。 |
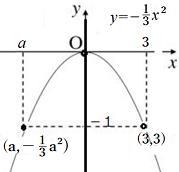
| 8⃣ 次の各問いに答えなさい。 (1) y=- a, bにあてはまる数を求めなさい。 |
| 8⃣の(1) 解説と答 簡単な図を書いてみよう。 -12≦y≦b よりx軸上のa座標は-3より 小さい値であることがわかる。右図のように 座標上に、知りえたデータを書き込みます。 条件よりb=0 y=- 成り立ちます。計算して,a=±6 a=6は問いにあわないので(a<0)、 a=-6,b=0…答 |
 |
| 8⃣-(2) 2つの関数 y=-2x²と y=-2x-4につ いて,x の値が a から a+3 まで増加するときの 変化の割合が等しいとき、aの値を求めなさい。 |
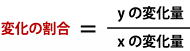
夏休み課題
| 袋の中に同じ重さのあめ玉がたくさんあり、その重さは1kgでした。 袋から10個のあめ玉を取り,重さを量ったところ40gでした。 袋の中のあめ玉は全部で何個ありますか。比例式を作ってときなさい |
10個のあめ玉の重さを合わせると40gです。
袋の中の取るまえの全体の個数をxとおいてみましょう。
1000:40 = x:10 x=250 全体の個数=250個
解説)左辺の1000:40は重さの比例式(比較)です。
右辺の x:10は個数の比例式(比較)です。
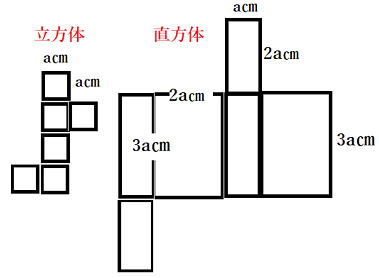
| 1辺acmの立方体Aの表面積は、縦a cm、横2a cm、高さ3a cmの 直方体Bの表面積の何倍でしょうか。 |
答 Aの表面積…6a²
Bの表面積は以下、3種類の面ができます。(下の図)
仮にaを5㎝として実際に直方体をつくってみましょう。
以下… a✕2a⇒2面 a✕3a⇒2面 2a✕3a⇒2面
4a²+6a²+12a²=22a²
立方体Aの表面積は直方体Bの表面積の何倍かなので、
6a²÷22a²=6/22 よって 3/11倍…答
注意)直方体Bの表面積は立方体Aの表面積の何倍かという問いなら
11/3倍です。問いの内容をしっかり把握すること。
また体積の比較でなく、表面積の比較であることにも注意‼
![]()
![]()
中3の学習に入るまえに以下の計算をやってみよう。
| 練習問題 次の計算をしなさい。□の中に数字を入れなさい ① 2= ⑤ |
いずれも暗算でできる問題です。難しく考えないこと。
① ![]() =
=![]()
| 復習問題1 次の計算をしなさい。 ① 15÷(−3)+2= ② −22+(−3)2= ③ |
| 復習問題2 次の1次方程式を解きなさい。
① x+9=0 ②
x−7=6 ③
x+12=0 ④ 3+
x=−7 ⑤
x−5=−11 ⑥ x−17=−9 |
|
復習問題3 次の1次方程式を解きなさい。 ① 5x=20 ② −4x=8 ③ 9x=−45 ④ −4x=−20 ⑤ 2x−5=−11 ⑥ x−17=−9 |
| 復習問題4 次の式を展開しなさい ① 2(a+3) ② (a+2)(b+1) ③(x+2)(x+1) ④ (x+2)(x−1) |
解説
① 2(a+3) のカッコをはずす場合、分配の法則を使って ![]() =2a+6
=2a+6
② (a+2)(b+1) は分配の法則を使って 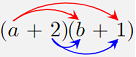
よって ab+1a+2b+2 → ab+a+2b+2 ※ 1aの1は省略します
③ 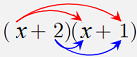 ④
④ 
| 復習問題5 次の計算をしなさい。
(1) 3x (2x + 3) (2) (a − 3b)×2b (3) −4a(a − 3b) |
解説 まず、( )内を因数分解したのち、2xで割ったら楽だよ。
(6) (3a − 6b)× ![]() a
a
3(a− 2b)×![]() a= a(a− 2b)= a2 − 2ab
a= a(a− 2b)= a2 − 2ab
(7) (8x2 + 6xy)÷2x
2x(4x+3y)÷2x=4x+3y
(8) (12ab+3b2) ÷ 3b
3b(4a+b)÷3b=4a+b
(9) (5x2 + 15xy− 10x)÷5x
5x(x+3y− 2)÷5x=x+3y− 2
=6
| 復習問題6 ① a=−2,b=3のとき 4a−5b−(a−4b)の値を求めよ。 ② ③ |
① 4a−5b−(a−4b)を展開すると、3a−b
になります。この式にa=−2,b=3を代入すると、
3a−b=−6−3=−9 …答
| 復習問題7 次のア~オの方程式のうち、 ア x−3=1 イ 3x=6 ウ 2x+1=5 エ 2x−3=x オ |
p22
| 復習問題8 xの値を求めよ ① x:10=1.5 : 5 ② 7:2=14:(x−5) |
p22
|
復習問題9 次の連立方程式を解きなさい。 (1)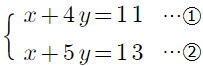 (2) (2)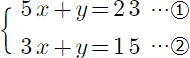 (3) (3)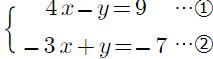 (4) 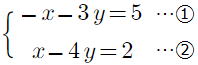 (5) (5)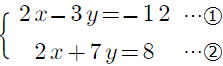 (6) (6)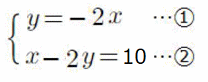 (7) 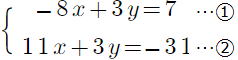 (8) (8) 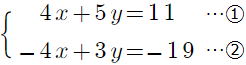 (9) 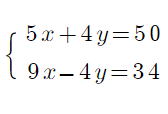 (10) (10)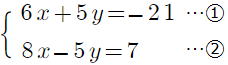 |
(1)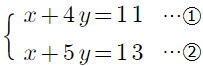 x=3,y=2 (2)
x=3,y=2 (2)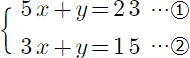 x=4,y=3
x=4,y=3
(3)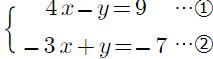 x=2,y=−1 (4)
x=2,y=−1 (4)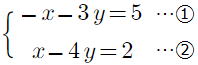 x=−2,y=−1
x=−2,y=−1
(5)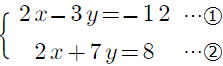 x=−3,y=2 (6)
x=−3,y=2 (6)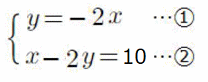 x=2,y=−4
x=2,y=−4
(7)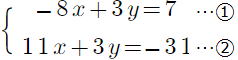 x=−2,y=−3 (8)
x=−2,y=−3 (8)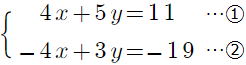 x=4,y=−1
x=4,y=−1
(9)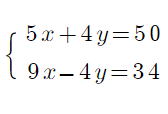 x=6,y=5 (10)
x=6,y=5 (10)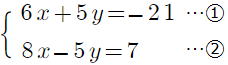 答 x=−1,y=−3
答 x=−1,y=−3
| 復習問題10 次の数量の関係を等式や不等式で表しなさい。 (1) 2数aとbの差の4倍はcより大きい。 (2) 500mの道のりを毎分80mでx分間歩くと、残りは70mになった。 (3)1個a円の品物を3割引きで5個買うと、代金は1万円以上になった。 |
答
(1) 2数aとbの差の4倍はcより大きい。
4(a-b)>c
(2) 500mの道のりを毎分80mでx分間歩くと、残りは70mになった。
500-80x=70
(3)1個a円の品物を3割引きで5個買うと、代金は1万円以上になった。
0.7a×5>10000 より 3.5a>10000
■式の計算/展開 ![]()
![]()
■乗法の公式を使った展開
| もっと楽な計算はないか?そこで使うのが、以下の乗法の公式です。 この方法は数学を学習するうえで非常に大切ですから数学が苦手な人も、ここは押さえておきたい個所です。 高校に進学してからも |
▲ 展開
![]() …公式
…公式
実際にやってみましょう。たとえば、
![]()
![]() では
では
![]()
![]() =
=![]() =x2+6x+8
=x2+6x+8
掛けて8、たして6になります。
展開の逆が因数分解と考えていいでしょう。では、因数分解について学習しましょう。
因数分解ができたらしめたもの、方程式も楽にできます。
これから乗法公式を
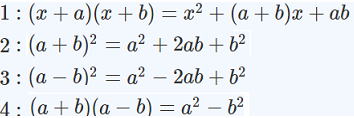
非常に大切な公式で高校に進学しても使います。
以下に説明していますが、実際の問題で数多く解くことが鍵です。
まず1.の (x+a)(x+b)= です
いままでは分配の法則を用いて、
(x+a)(x+b) や (a+b)(c+d)を
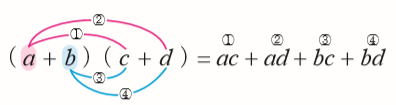
のように計算していました。面倒でしたね。
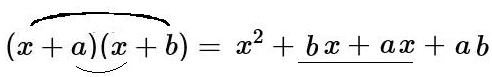
アンダーラインの個所を (a+b)x のように、直接足します。
実際の式 (x+1)(x+2)を展開してみましょう?
(x+1)(x+2)の展開 いままでは
x2+2x+1x+2 = x2+3x+2 と計算していたのを、
アンダーラインの個所を
2x+1x =3x と、楽して計算するのが乗法公式です。
図に書くと
(x+□)(x+△) =x2+(□+△)x+□△
(注 □△は□×△のことです)
| 例1 (x+3)(x+2) = □=3 △=2と置き換えると (x+□)(x+△) = x2+(□+△)x+□△ (□+△)は 3+2=5 ですから x2+5x+6 になります。 |
| 例2 (x+3)(x−2) = □=3 △=−2と置き換えると (x+□)(x−△) = x2+(□+△)x+□△ (□+△)は 3+(−2)=1 ですから x2+1x+6 になります。 (x−2)(x+3)も因数の順番が変わっただけで同じですね。 |
次の式を乗法の公式①を使って、展開してみよう。
| 例題 ① (x+1)(x+2)=x2+3x+2 ② (x+1)(x+3)=x2+4x+3 |
① たして3、掛けて2 ② たして4、掛けて3
こうした問題は数多くやることが大切です。ミスも少なくなるし、スピーディになります。
| 問1 次の式を乗法の公式を使って、展開しなさい。 (1) (x+3)(x+2) (2) (x+3)(x−2) (3) (x+2)(x−1) (4) (x+1)(x−2) (5) (x−2)(x-3) (6) (y+1)(y−2) (7) (x−6)(x+2) (8) 3x(x−6) (9) (x+6)(x
+2) |
答
(1) (x+3)(x+2)= x2+5x+6 (2) (x+3)(x−2)= x2+x−6
(3) (x+2)(x−1)= x2+x−2 (4) (x+1)(x−2)= x2−x−2
(5) (x−2)(x-3)= x2−5x+6 (6) (y+1)(y−2)= y2−y−2
それでは公式②、③を使った展開に進みましょう。
◆公式②,③
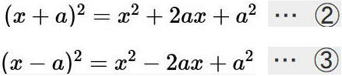
具体的な数値を代入して、やってみましょう。
以下はいままで通りの展開です。
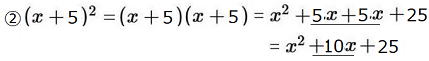
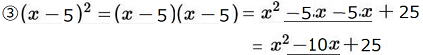
・②の (x+5)2は5とxをかけ、それを2倍します。
(5x)×2=10x
・③の (x−5)2は −5とxをかけ、それを2倍します。
(−5x)×2= −10x ※これがキーポイント
実際にやってみましょう。
| 次の式を展開しなさい。 ① (x+1)2 ② (x+2)2 ③ (x+3)2 ④ (x-1)2 ⑤ (x-2)2 ⑥ (x-3)2 ⑦ (x+5)2 ⑧ (x+4)2 ⑨ (x+6)2 ⑩ (x-4)2 ⑪ (x-6)2 ⑫ (x-5)2 ⑬ (2x+1)2 ⑭ (3x+1)2 ⑮ (2x-1)2 ⑯ (3x-2y)2 |
| 公式④ (x+a)(x−a) = x2−a2 |
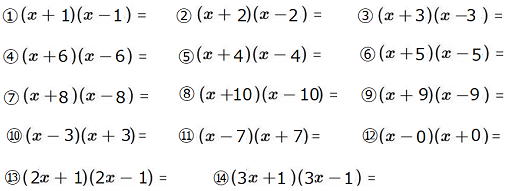 |
※「乗法の公式を使わなくても良いじゃないか。せっかく分配の法則を勉強したし…」
ってと思う生徒さんもおられるでしょう。
でも、しつこいようですが、この公式は便利なうえ、非常に大切なんです。
高校に進学してからも、
できるできないの違いは「頭の良し悪し」じゃありません。
数多くの問題にチャレンジするかしないかの違いです。
乗法の公式 もっとやる へ TOPへ戻る
■因数分解 ![]()
因数とは… たとえば 21=7×3で、7や3を因数といいます。
21を3×21に因数分解しました。
同様に21=1×21も1と21に因数分解できます。
中1で学習した 2x+2=2(x+1) の2やx+1も因数といいます。
(x+3)(x−2)の (x+3)や(x-2)なども、それぞれを因数といいます。
因数分解とは… 2x+2=2(x+1)のように整理する?ことを因数分解といいます。
x2−xを因数分解すると x(x−1) で、xと(x−1)の因数になります。
〇因数分解(復習)
| 例題 ① 2ay+3a ② 7x−7y+7 ③2x2−18x |
① 2ay+3a 各項にaが共通にかけられているのでaだけ前にくくりだします。
2ay+3a=a(2y+3) …答
② 7x−7y+7 7が共通因数となっているのでyを前にくくりだします。
7(x−y+1) …答
③ 2x2−18x=2x(x−9 ) …答
2とxが共通因数となっているので2xを前にくくりだします。
因数分解した答を展開すると、そのまま問いと同じになります。
たとえば、問1の① 2ay+3a を因数分解すると、a(2y+3)…答
この答を展開すると、元の2ay+3a になります。
| 問 因数分解しなさい ① 3a+3c ② ax+5a ③ 2y+14 |
〇乗法公式の公式を使った因数分解
図1は展開、下の図2は因数に分解する(因数に整理する)公式です。


上の図1は、乗法の公式で最初にみた公式ですね。
以下は左辺と右辺を逆にした公式です。下図のように、

因数分解とは、それこそ因数に分解することです。
展開の反対が因数分解、因数分解の反対が展開 と考えていいでしょう。
ところで、 ![]() …① でしたね
…① でしたね
![]() =
=![]()
![]() …②
…②
①式と2⃣式で左辺と右辺が逆になっているのを確認してください。
②の ![]() や
や![]() をそれぞれ因数といいます。因数分解とは因数ごとに整理することです。
をそれぞれ因数といいます。因数分解とは因数ごとに整理することです。
たとえば ![]()
![]() を展開すると、
を展開すると、
![]()
![]() =
=![]() =x2+6x+8 になりました。
=x2+6x+8 になりました。
反対にx2+6x+8 を因数分解すると、![]()
![]() になります。
になります。
ややこしい説明はさておいて、実際の問題で理解しましょう。
▲公式①を使った因数分解
① (x+2)(x+3)を展開すると x2+5x+6 でしたね。
反対にx2+5x+6を因数分解すると (x+2)(x+3) になります。
それでは①式はどのように因数に分解するのでしょう。
まず、x2+5x+6 の6に注目 ふたつの数を掛けて6、
次に足して5x の5になるには?
6と1では7、2と3では5 掛けて6、足して5になりましたね。
最初はx2なので(x+〇)(x+□) とおき、
〇と□にそれぞれ2と3を代入し、
(x+3)(x+2) となります。
※ (x+3)(x+2) のように因数の順番が反対でもOKです。
次に、マイナスが入った x2+x−6 について考えてみましょう。
3と2を掛けても−6にはなりません。
−3に2を掛けるか、−2に3を掛けると−6になりますね。
そこで足したらx (1xのこと) +1になるには?
1と6ではなりませんね。じゃあ3と −2だったら?。
そう。1になります。 (x+3) と (x−2) に因数分解できました。
x2+x−6=(x+3)(x−2)
公式①を用いた因数分解
| 問1 以下は公式①を使った問題です。因数に分解(整理)してみよう。 ① x2- 4x−12= ② x2+3x+2= ③ x2- x−2 ④ x2+ 4x + 3= ⑤ x2 +2x−3= ⑥ x2−2x−3= |
x2- 4x−12=(x−6)(x+2) …答
この答を展開すると、元のx2-4x−12になることを確認してください。
②x2+3x+2=
掛けて2、足して3になる数は?
掛けて2、足して3だから1と3 (x+1)(x+2) …答
(x+2)(x+1)でもOKです。
▲ 公式②,③を用いた因数分解
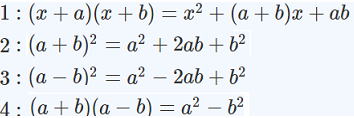
| 問 以下は公式②,③を使った問題です。因数に分解(整理)してみよう。 ① x2+14x+49 ② x2+16x+64 ③ x2+12x+36 ④ x2-14x+49 ⑤ x2- 6x+9 ⑥ x2-12x+36 ⑦ x2+ 24x+144 ⑧ x2+ 20x+100 ⑨ x2+ 22x+121 |
答
① x2+14x+49 = (x+7)2 ② x2+16x+64 = (x+8)2 ③ x2+12x+36 = (x+6)2
④ x2-14x+49 = (x-7)2 ⑤ x2-6x+9= (x-3)2 ⑥ x2-12x+36 = (x-6)2
▲ 公式④を用いた因数分解
| 問 以下は公式④を使った問題です。因数に分解(整理)してみよう。 ① x2−9 ② x2−49 ③ 49−x2 ④x2−4 ⑤x2−16 |
| 応用問題 以下の①~⑲の式を因数分解しなさい。 |
| ① 3x2 −7xy2+8xy |
まずxを( )の外に出そう‼。それ以外に( )の外に出すモノはない。
あとは何も考えていない。(少なくともボクはそれ以外何も考えていない)
3x2 −7xy2+8xy=x(3x−7y2+8y)
下の図のように、展開しながら、因数分解すると間違いないよ。
2a+6=![]() ab+a+2b+2=
ab+a+2b+2=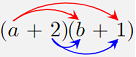
とりあえず因数分解してみた。これ以上因数分解できないね。これが答だ。
| ② a3 +2a2b2−9ab |
まずa を( )の外に出そう‼
a(a2 +2ab2−9b) これ以上因数分解できないね。これが答です。
| ③ 5x2y3z −15xy2z3−10x3yz2 |
まずxyzがすべてに共通しているので、xyzを( )の外に出そう‼。あっ、それに5も()のそとに出せる。
あとは何も考えない。とにかく、5xyzを( )の外に出す。
5x2y3z −15xy2z3−10x3yz2 =5xyz(xy2−3yz2−2x2z)
これ以上因数分解できない。これが答
それにしてもいやらしい問題が続くね。
まったくイヤになる。ため息が出る。しかし、これも試練。イヤでもやるっきゃない。
| ④ 6x3y −12x2y+42xy2−18xy |
なにを( )の外に出すか?
6とxとyかな? そう、6とxとyだね。
6x3y −12x2y+42xy2−18xy =6xy(x2−2x +7y−3) …答
こうした複雑な問題を解く場合、因数分解しながら、右辺に因数分解しながら展開し、
ミスってないか絶えず調べることが大切です。 しかし、イヤな問いだね。
学校の先生が作成した問題ではないね。でも、数学では緻密で正確な解答が求められます。
| ⑤ x2+12x−108 |
ようやくホッとする問題になったね。
かけて108、絶対値を足して12は? 4と27かな?(×)。 では6と18ではOK
x2+12x−108=(x+18)(x−6) …答
| ⑥ a2−33a+90 |
かけて90、絶対値を足して33は? 9と10?(×だね) 3と30?(当たりーっ)
a2−33a+90=(a−3)(a−30) …答
| ⑦ y2+4y−96 |
かけて96、絶対値を足して4は?まるで数当てクイズだね。
3と32?(×だね) もっと大きい数だ。じゃあ、6と16?(ブ、ブーッ)
8と12? これだっ!
(y−8)(y+12)…答
| ⑧ x2+12x−108 |
かけて108、絶対値を足して12は? 6×18 (いきなりOKみたい)
(x−6)(x+18) 展開して元の式になるのでOK (x−6)(x+18) …答
| ⑨ x2+10xy+21y2 |
xの関数にy がくっついた」ぐらいに考えて良いと思う。
かけて21,絶対値を足して10は?
7×3かな?(おーっ、良さそうだ)
x2+10xy+21y2 =(x+3)(x+7)
展開すると…ブ、ブーッ。 そう、yを忘れてるね。
x2+10xy+21y2 =(x+3y)(x+7y) …答
展開すると、元の式になるよね。
| ⑩ x2−3xy−40y2 |
かけて40y2, 絶対値を足して3は?そう、5yと8yだね。
x2−3xy−40y2 = (x−8y)(x +5y) …答
答を展開して元の式になるかな?なったら正解!
| ⑪ x2−9xy+18y2 = |
x2−9xy+18y2 = (x−3y)(x −6y) …答
| ⑫ x2−7xy+12y2 = |
x2−7xy+12y2=(x−4y)(x −3y) …答
足して−7y, かけて12y2になるね。
⑬ x2+8xy−20y2 = (x+10y)(x −2y) …答
⑭ x2−![]() y2 =
y2 =
同じ数をかけて ![]() y2 は
y2 は ![]() y×
y×![]() y
y
(x + ![]() y)(x −
y)(x −![]() y)…答
y)…答
| 1~4までの公式の4を使います。覚えていますか? (右の公式を参考) |
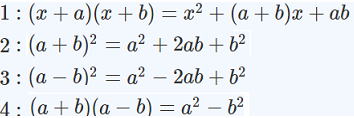 |
以下、(19)まで公式4を使います。
⑮ 64p2−121=(p+11)(p−11) …答
⑯ 4y2−81=(2y+9)(2y−9) …答
⑰ 9x2−y2=(3x+y)(3x−y) …答
⑱ 81a2−169b2=(9x+13b)(9x−13b) …答
⑲ 144x2−25y2=(12x+25y)(12x−25y) …答
TOPへ戻る
■素因数分解
72は8×9と表せるので8と9は、72の因数である。
また,72は6×12と表せるので、6と12は因数である。
2,3,5,7などは、それより小さい自然数の積の形で表すことができません。
このような2,3,5,7などの自然数を素数といいます。
ただし、1は素数に含まれません。
素数である因数を素因数といい、
自然数を素数の積として表すことを素因数分解する、といいます。
| 問 1から20までの素数をすべて書きなさい。 |
答 3, 5. 7, 11, 13, 17, 19
それでは素因数分解してみましょう。
| 例1 それでは84を素因数分解してみましょう。 右のように、素数で次々に割っていくことによって、 84=2×2×3×7=22×3×7 が得られます。 |
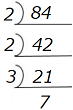 |
| 例2 120を素因数分解してみましょう。 120=23×3×5 が得られます。 |
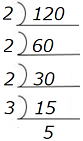 |
23×3×5=
| 問1 360を素因数分解しなさい。 |
答  360=23×32×5
360=23×32×5
| 問2 次の数を素因数分解しなさい。 (1) 80 (2) 96 (3) 288 (4) 250 |
答
(1) 80=24×5 (2)96=25×3 (3)288=25×32 (4)250=2×53
▲色々な因数分解
| 例1 ax2+ 6ax−16a を因数分解しよう |
ax2+6ax−16a=a(x2 +6x−16)= a(x+8)(x−2)
| 例2 (x−1)y− (x−1) を因数分解しよう |
| 例3 (x+2)2− 3(x+2)− 4 を因数分解しよう |
| 問1次の式を因数分解しなさい。 ① 2x2−x ② ( 9a2b−3ab ) ÷ (− ④ (x−2)2−3(x−2)+2 ⑤ (x+y)2−4 ⑥ (x−y)2+ 4(x−y)−5 |
▲式の計算の利用
| 例1 172−132 を因数分解を利用して計算してみよう |
172−132= (17+13)(17−13)= 30×4=120
-------------------------------------------------------
| 例2 以下の式を計算してみよう ① 192 ② 77×83 |
答 ① 192=(20−1)2 =202−2×20+1=400−40+1=361 (x−y)(x+y)=x2−y2 ② 77×83=(80−3)(80+3)=802−32=6391 |
| 例3 x=11, y=2のとき、次の式の値を求めなさい (x−2y)(x + 2y)−(x−y)(x + 4y) |
解説) まず展開しよう。
| 問 x=198のとき、x2+4x+4の値を求めなさい |
解説) まず、与えられた式を因数分解しよう。
------------------------------------------------------
| 問 (1)2つの連続した奇数の積に1をたすと4の倍数になる。 (2)2つの連続する奇数の平方の差は8の倍数になる。 (3)3つの連続した偶数では最も大きい数の平方から残りの2つの数の積をひいた差は4の倍数になる。 |
(1) mを整数として2つの連続した奇数を 2m−1, 2m+1 とする。
それらの積に 1 をたすと、
(2m−1)(2m+1)+1=4m2−1+1=4m2
m は整数なので m2も整数。
よって4m2は4の倍数となる。
別解)nを整数として2つの連続した奇数を 2n+1, 2n+3 とする。
(2n+1)(2n+3)+1=4n2+8n+4
=4n2+8n+4=4(n2+2n+1)=4(n+1)2
n は整数なので (n+1)2も整数。
よって4(n+1)2は4の倍数となる
(2) mを整数として2つの連続した奇数を2m-1, 2m+1とする。
平方の差は
(2m+1)2-(2m-1)2=4m2+4m+1-(4m2-4m+1)=8m
m は整数なので 8m は 8 の倍数となる。
(3) mを整数として、3つの連続した偶数を2m, 2m+2, 2m+4とする。
もっとも大きい数の平方から残りの2数の積を引くと
(2m+4)2−2m(2m+2)=4m2+16m+16−4m2−4m=12m+16=4(3m+4)
mは整数なので3m+4 も整数となり4(3m+4) は4の倍数となる。
■式の計算の利用
以下の問いにチャレンジしよう‼
|
整数n,またはmを用いて数式を組み立ててみよう。 ② 2つの偶数 ※2つの偶数は連続していないので2種類の文字を使う
③ 連続する3つの整数 ④ 連続する3つの偶数 ⑤ 連続する3の倍数 ⑥ 2つの奇数の積に1を加えた数 |
答
問1 連続する2つの奇数
nを整数とすると2n-1, 2n+1 (2n+1, 2n+3も可)
問2 2つの偶数
問3 連続する3つの整数
問4 連続する3つの偶数
問5 連続する3の倍数
問6 2つの奇数の積に1を加えた数
n,mを整数とすると(2n+1)(2n+1)+1
問7 連続する3つの整数の平方の和から1をひいた数
nを整数とすると(n-1)2+n2+(n+1)2-1
| 問1 x2+2x+a を因数分解すると、(x+3)(x+m) になるという。 mとaの値を求めなさい |
x2+(3+m)x+3m = x2+2x+a だから 3+m=2, 3m=a
よって m=-1 , a=-3…答
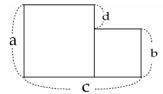
| 問2 次のことがらを証明しなさい。 (1)右図のように1辺の長さがa,bの大小2つの正方形が並べてある。 この2つの正方形の面積の差はc,dの積に等しい。 (2)2つの連続した奇数の積に1をたすと4の倍数になる。
(3)2つの連続する奇数の平方の差は8の倍数になる。 (4)3つの連続した偶数では最も大きい数の平方から残りの2つの 数の積をひいた差は4の倍数になる。 |
 |
積はかけ算、平方は2乗のことです
(1) この 2 つの正方形の面積の差は a2−b2 …①
c=a+b , d =a−b なので c と d の積は
c × d =(a+b)(a−b)=a2−b2…②
①、②より、この 2 つの正方形の面積の差はc,dの積に等しい
(2) mを整数として2つの連続した奇数を 2m−1, 2m+1 とする。
それらの積に 1 をたすと、
(2m−1)(2m+1)+1 = 4m2−1+1=4m2
mは整数なので m2も整数。
よって4m2は4の倍数となる。
(3) mを整数として2つの連続した奇数を2m−1, 2m+1とする。
平方の差は
(2m+1)2−(2m−1)2 = 4m2+4m+1−(4m2−4m+1)=8m
m は整数なので 8m は 8 の倍数となる。
(4) mを整数として、3つの連続した偶数を2m, 2m+2, 2m+4とする。
もっとも大きい数の平方から残りの2数の積を引くと
(2m+4)2−2m(2m+2) = 4m2+16m+16−4m2-4m = 12m+16= 4(3m+4)
mは整数なので3m+4 も整数となり4(3m+4) は4の倍数となる。
| 問3 2つの連続する偶数の積に1を加えた数は、奇数の平方になることを証明しなさい。 |
証明/解説
積はかけ算、平方は2乗のことです
証明
整数をnとおき、2つの連続する偶数を2n, 2n+2と表す。
2つの連続する偶数2n, 2n+2をかけ算して1を加える。
これらの2数の積に1を加えると、
2n(2n+2)+1=4n2+4n+1=(2n+1)2
nは整数なので2n+1は奇数である。
したがって2つの連続する偶数の積に1を加えた数は、奇数の平方になる
以下は福岡県入試問題です。
| 問4 異なる2つの奇数において、大きい方の奇数の2乗から小さい方の奇数の2乗をひいた差は、4で割り切れることを証明しなさい。 (H27) |
証明)
異なる2つの奇数をm,n(m,n:整数)とすると、
大きい方の奇数は2m+1
小さい方の奇数は2n+1 とおける
(2m+1)2−(2n+1)2
=(4m2+4m+1)−(4n2+4n+1)
=4(m2+m−n2−n)
(m2+m−n2−n)は整数だから、4(m2+m−n2−n)は4で割り切れる。
したがって、
大きい方の奇数の2乗から小さい方の奇数の2乗をひいた差は、4で割り切れる
問4
| 右の表は2から50までの偶数を順に並べたものである。 下の表は右の表の一部を4つの偶数の数字をわくで抜き取った ものである。4,6,14,16や 16,18,26,28のように、かっこ内の4つの偶数において、 最も大きい数と2番目に小さい数の和の2乗から、2番目に大きい数と最も小さい数の和の2乗を引いた差は32で割り切れことの証明を文字を使って、以下を証明を完成させなさい。
|
(H26) |
||||||||||||||||||||||||||||||||||
| 証明 したがって、4つの偶数において、最も大きい数と2番目に小さい数の和の2乗から、2番目に大きい数と最も小さい数の和の2乗を引いた差は、32でわりきれる。 |
|||||||||||||||||||||||||||||||||||
最も小さい数を2n(n:整数)と表すと、2番目に小さい数は2n+2、
順に2n+10,2n+12と表せる。
最も大きい数と2番目に小さい数の和の2乗は{(2n+12)+(2n+2)}2
2番目に大きい数と最も小さい数の和の2乗は{(2n+10)+(2n)}2
{(2n+12)+(2n+2)}2 −{(2n+10)+(2n)}2 これを計算すると、
(4n+14)2 −(4n+10)2=16n2+112n+196−(16n2+80n+100)
=32n+96=32(n+3)
n+3は整数だから32(n+3)は32でわりきれる。
したがって、4つの偶数において、最も大きい数と2番目に小さい数の和の2乗から、
2番目に大きい数と最も小さい数の和の2乗を引いた差は、32でわりきれる
■二次方程式 ![]() 因数分解ができたら、方程式は簡単‼
因数分解ができたら、方程式は簡単‼
例えば上の問題④の答えは ![]() +
+![]() -6 =(
-6 =(![]() +3)(
+3)(![]() +2)ですね。
+2)ですね。
④は因数に分解したので、これが方程式になると、
「x2+x-6 =0の2次方程式を解け」 のような問いになります。
x2+x-6 =0=0 は (x +3)(x-2)=0 に因数分解できるね。
(x +3)=0, (x-2)=0 それぞれの因数から x= -3と x=2 x=-3 , 2…答
それでは実際に2次方程式を解いてみよう。 まず因数分解から、ね!
| 問 次の2次方程式を解きなさい ① x2+8x+7=0 ② x2+4x+4=0 ③ x2-5x+6=0 ④ x2-9=0 ⑤ x2+3x-18=0 ⑥ x2-5x-36=0 ⑦ x2-49=0 ⑧ x2+7x+10=0 ⑨ x2-10x+25=0 ⑩ x2+12x+36=0 ⑪ x2-5x-24=0 ⑫ x2+12x+36=0 ⑬ ⑯ x2+5x−24=0 ⑰ x2+x-12=0 ⑱ x2-9x+14=0 ⑲ x2+14x+49=0 ⑳ x2-16x+64=0 |
解説)①を解いてみましょう。中学で学習する方程式は1次方程式と2次方程式がありますが、
中3では2次方程式を学びます。
x2+8x+7=0 まず左辺を因数分解します。
x2+8x+7=0 (x+1)(x+7)=0
(x+1)=0と (x+7)=0の場合が考えられます。
まず(x+1)=0のとき、 x+1=0からxを求めるには1を右辺に移項します。よってx=-1
同様に (x+7)=0 x=-7 x=-1,-7 …答
■復習問題 展開 ⇆ 因数分解 方程式
▲展開
| 問1 式を展開しなさい ① (2x+1)2 ② (3x+2)2 ③ (3x+2)(x−1) ④ (2x+3)(x−2) |
答 ① 4x2+4x+1 ②9x2+12x+4 ③ 3x2−x−2 ④ 2x2−x−6
⑤ x2−4x+4 ⑥ x2−4xy+4y2 ⑦ x2−x−2 ⑧ x2+6xy+9y2
⑨ x2−6x+9 ⑩ x2 −4 ⑪ x2+10x+25 ⑫ x2−10x+25
⑬ x2 −16 ⑭ x2+8x+16 ⑮ x2−8x+16 ⑯ x2−5x+6
⑰ x2-x-6 ⑱ x2+12x+36 ⑲ x2−12x+36 ⑳ x2 − 25\
▲因数分解
| 問1因数分解しなさい ① 3a+3c ② ax+5a ③ 2y+14 |
| 問2 因数分解しなさい。 ① x2+2x+1 = ② x2+4x+4 = ③ x2+x−2 = ④ x2+x−6 = ⑤ x2−4x+4 = ⑥ x2−2x+1 = ⑦ x2−x−2 = ⑧ x2+6x+9 = ⑨ x2−6x+9 = ⑩ x2 −4 = ⑪ x2+10x+25 = ⑫ x2−10x+25 = ⑬ x2 −16 = ⑭ x2+8x+16 = ⑮ x2−8x+16 = ⑯ x2−5x+6 = ⑰ x2-x-6 = ⑱ x2+12x+36 = ⑲ x2ー12x+36 = ⑳ x2 − 25 = |
| 問3 因数分解しなさい。 ①x2−25 ②25−x2 ③ 81−x2 ④ x2+5x−6 ⑤ x2+13x+40 ⑥ x2+8x+16 ⑦ x2−18x+81 ⑧ x2−121 ⑨ 36−x2 ⑩ x2−13x+40 ⑪ x2−5x−6 ⑫x2+5x+6 |
| 問4 因数分解しなさい。 ① ax+bx ②12ax−6bx ③3mn+12m ④ab+ac+ad ⑤2m2+6mn ⑥ x2−2x ⑦ x2y+ |