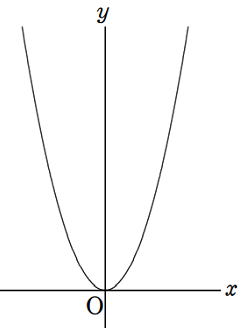
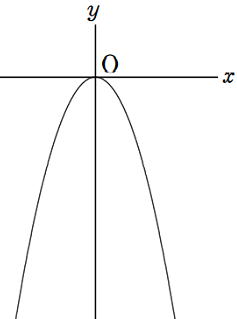
中学では以下①~③の3つのグラフを学びます。
①比例(直線、一次関数) ※以下youtubeを参照。説明がとても分かりやすいですね。
1次関数1 y=ax+b (youtube)
1次関数2 変化の割合
1次関数3 グラフの書き方1
1次関数4 傾きと切片
1次関数5 グラフの書き方2
②反比例 (双曲線)
③2次関数のグラフ(放物線) y=ax2
比例、反比例は中1から中2で学習しました。
これから2次関数のグラフを学んでいくうえで、比例(一次関数)のグラフは大切ですので、
ここでしっかり理解しておきましょう。
中学で学ぶ3つのグラフについて見てみましょう。もし、忘れていても心配する必要はありません。
| [基本問題をやってみよう] これが分かれば中学で学習するグラフもそう難しくないよ。 難解な問いもたまに、あるけど心配ご無用! 問1 x=2のとき、次の式のyの値は?。 ① y=2x ② y=-2x+1 ③ y=3x-1 ④ y= ⑤ y=x2 ⑥ y= 2x2 ⑦ y= 問2 上の問い①~④の傾きと切片を答えなさい。 ①傾き( ) 切片( ) ②傾き( ) 切片( ) ③傾き( ) 切片( ) ④傾き( ) 切片( ) 問3 x=2, y=2のとき、以下の比例定数=aの値を求めなさい。 ① y=ax ② y=ax+1 ③ y=ax-1 ④ y=ax+2 ⑤ y=ax2 問4 ① ㋐ y=2x-4 ㋑ y= ② 8x+2y-3=0の切片と傾きを答えよ。 ヒント:グラフの式に変えよう ③ 次の中から右上がりのグラフになる式をすべて選び記号で答えよ。 ㋐ y=3x+5 ㋑ y=-x+12 ㋒ y=5x-8 ㋓ y=27x-1 ㋔ y=-3x-5 ④ y=3x+1のグラフと平行なグラフの式を選んで記号で答えなさい。 ㋐ y= 3x+11 ㋑ y=-3x+5 ㋒ y=13x+4 ㋓ y=-13x+2 ⑤ 3x+6y+24=0のグラフと平行なグラフの式を選んで記号で答えよ。 ㋐ y=3x+5 ㋑ y=-3x+2 ㋒ y=2x-4 ㋓ y=- |
問3の答 ① a=1 ② a=![]() ③ a=3/2 ④ a=0 ⑤ a=
③ a=3/2 ④ a=0 ⑤ a=![]()
以下の3つの公式
①比例 y=ax+b, ②反比例![]() , ③2次関数 y=ax2は必ず覚えよう。
, ③2次関数 y=ax2は必ず覚えよう。
| 比例 (式) y=ax+b | 反比例 (式) |
2次関数 (式) y=ax2 |
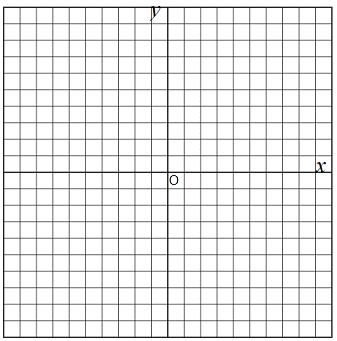
a >0のとき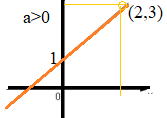 a <0のとき 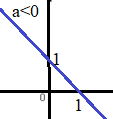 |
下図は比例定数が正 a >0のとき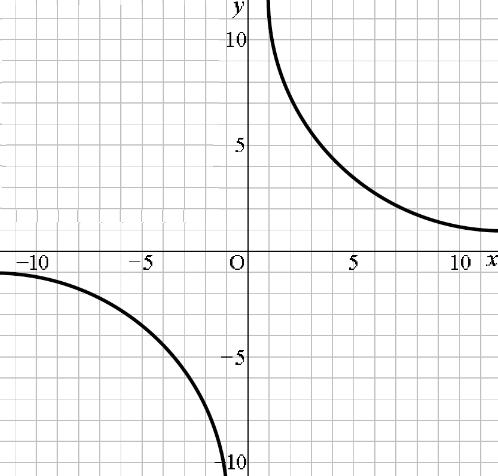 |
下図は比例定数が正 a >0のとき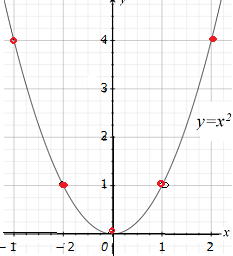 |
具体的な数値で表してみよう
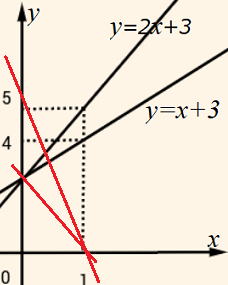
| 黒の直線はそれぞれ比例定数 (傾き)2と1、切片3の直線グラフです。 赤の直線グラフは?(下に解答) |
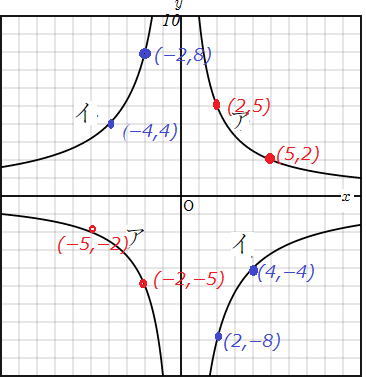
●アの双曲線はa>0 ●イはa<0のときのグラフです。 |
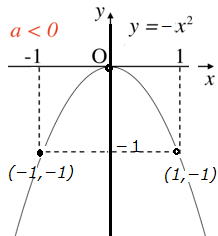
下のグラフはa<0 y=-x2 |
 |
 |
 |
赤の直線グラフは①は切片が5で傾きが-5だから y=-5x+5
②は切片が3で傾きが-3だから y=-3x+3 になります。
(1) 比例 一次関数のグラフ(1年/2年の復習)
「変化の割合」とは、
「xの値が変化した時に、yの値がどれくらい変化したかを調べ、
yの変化量をxの変化量で割った値」のことです。
 =傾き になります
=傾き になります
下のグラフは比例 y=ax (1年で学習)
a:傾き(比例定数) 直線は原点Oで接します。
右図はxが1増加したとき、yは2増加してるので から変化の割合は2。 から変化の割合は2。つまり傾きは2で、y=ax a=2でグラフの式はy=2xになります。 |
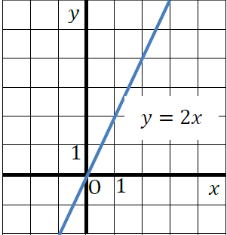 |
| y=ax のグラフの基礎的問題 問1 次の式は右のどのグラフを指しているでしょうか。 ( )の中に番号で答えなさい。 (1) y=2x ( ) (2) y=5x ( ) (3) y=−x ( ) (4) y=−4x ( ) |
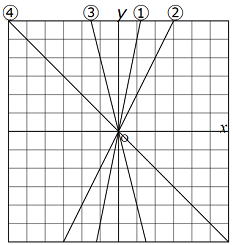 |
解答
| 右のグラフは1次関数直線 y=2x+3とy=x+3の式を表したものです。 y=ax+bのグラフ a:傾き(比例定数) b:切片(y軸と交わるところ) ここで、傾きと切片をしっかり理解しておきましょう。 |
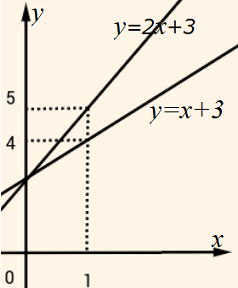 |
| 問2 次の式は右のどのグラフを 指しているでしょうか。 番号で答えなさい。 (1) y=−2x+6 (2) y=3x−2 ③ y= |
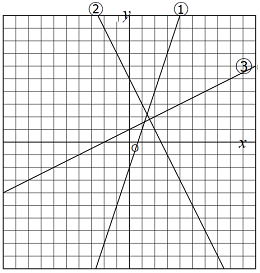 |
| y=ax+b のグラフ a:傾き(比例定数) b:切片 (y軸と交わる点) 問3 問2と同じ式です。 次の式をグラフに書き込みなさい ① y=3x−2 ② y=−2x+5 ③ y= |
 |
答 ① y=3x−2 ② y=−2x+5 ③ y=![]() x+1
x+1
 グラフ原本
グラフ原本
| 問4 以下のグラフ式を答えなさい。 ① 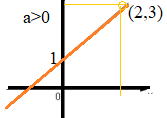 ② ②  |
まず、y=ax+bで考えよう。傾きは?。切片は?
| 問5 右図の赤線で引いた2本の1次関数の式を、それぞれ答えなさい。 |  |
この問いも同じ。まず、y=ax+bで考えよう。傾きは?。切片は?
| 問5 次の直線の式を求めよ。 (1)直線y=2xに平行で、(0,−3)を通る直線 (2)2点、(4,8)、(−3,−13)を通る直線 (3)点(−2,5)を通り、x軸に平行な直線 |
この問いも同じ。まず、y=ax+bで考えよう。傾きは?。切片は?
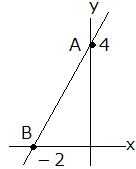
| 問6 p38 (1) 傾きが3で、点(0,2)を通る直線の式を求めなさい。 (2) 直線y =3x−2 に平行で、点(4,2)を通る直線は (3) 右図の直線ℓの式を求めなさい。 (4) 原点(0,0)と右図の線分ABの中点を通る直線の式は? |
 |
解説 グラフ原本
| (1) 傾きが3なので y=3x+bとおく 点(0,2)を通るので、 y=3x+2 (答) (2) 直線 y=3x−2 に平行で、点(4,2)を通る直線は 傾きが3なので y=3x+bとおく また、点(4,2)を通るので、2=12+b b=−10 よって、求める式は y=3x−10 (答) (3) 右図の直線ℓの式は 右図から傾き2 切片4であることが分かる よって、 y=2x+4 (答) (4) 原点(0,0)と右図の線分ABの中点を通る直線の式は ABの中点は(−1,2) y=ax 2=-a よって y=−2x (答) |
 |
| 問7 ①x=2のときy=7で、x=4のときy=11となるような1次関数の式を求めよ。 ② 2点 (2,9),(4,7)を通る直線の式を求めよ。 ③切片が3で点(-2, 11)を通る直線の式を求めよ。 ④点(1,6)を通り、直線 y=-x+3とx軸上で交わる直線の式を求めよ。 |
![]() ここらでひと休み
ここらでひと休み
| 右のグラフは反比例で a>0のときのグラフで、 |
 |
反比例の問題
問1 以下の式を右の図に書きなさい。 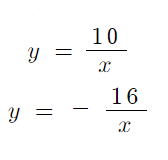 |
 |
 A,E,F
A,E,F
比例・反比例の利用 p34
| 問8 次の文のyをxの式で表しなさい。 (1) x㎞の道のりを時速50㎞で走るとy時間かかる。 (2) 底辺x㎝で面積が20㎠の三角形の高さはy㎝である。 (3)おもり1㎏につき0.5㎝伸びるバネに、x㎏のおもりを下げるとy㎝伸びる。 |
解説
(3) 二次関数のグラフ
yはxの2乗に比例するグラフ。y=ax2で表します。(a:比例定数)
下のグラフは2次関数。つまり、yはxの2乗に比例するグラフです。
関数 y=ax2 で表します。
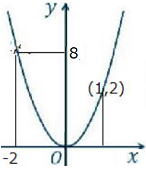
仮にa=2として、y=ax2 のグラフを書いてみましょう。
x=0ならy=0、x=1なら y=2、
同様にx=-1ならy=2、 x=2ならy=8
以下のようなグラフになります。 グラフ原本
|
 |
連続した線になりますが、実は無数からなる「点の集まり」なのです。
y=x2のグラフを書いてみよう。
|
 |
| 仮に比例定数 a=2として、y=2x2 のグラフを書いてみましょう。 |
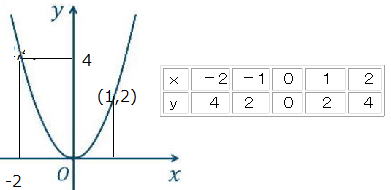
a<0の場合はどのようなグラフになるだろうか?
y=−x2 のグラフで考えてみよう。
|
 |
| 問 関数 y =5x2 について , x とy の関係をまとめると右の表のようになった。 次の問いに答えなさい。
|
答 (1) ① y = 5x2 式に x = 2 を代入すると, y = 5× 22 = 20
② y = 5x2 に x =5代入すると, y = 5× 52 = 125
(2)
| (3) 次の ① 〜⑤のそれぞれについて , y をx の式で表しなさい。 また , y が x の 2 乗に比例するものをすべて選び , 記号で答えなさい。 ① 半径 x ㎝の円の円周の長さ x㎝ ② 1辺が x ㎝の正方形の面積 y ㎠ ③ 底辺 10 ㎝, 高さ x ㎝の三角形の面積 y㎠ ④1辺が x ㎝の立方体の体積 y㎤ ⑤ 半径 x ㎝の円の面積 y㎠ |
(3) ①y= 2πx ②y =x2 ③y = 5x ④y= x3 ⑤y =πx2
| 問 yはxの2乗に比例し,x =3のとき y=-27です。 xとyの関係を式に表しなさい。 (北九市教育委員会) |
yはxの2乗に比例するから、まず、y=ax2 と置きましょう。あとは簡単!
y=ax2 にxとyの値を代入するだけ。 -27=32a
9a=-27 a=-3 よって y=-3x2
▲ 二次関数と一次関数の交点
※以下、出題率が高いです。なぜなら中学数学で学習した復習を問う問題だからです。
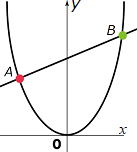
| 例1 右のグラフは2次関数y=x2 と y=x+6の一次関数の直線です。 交点AとBの座標を求めてみよう。 ここは連立方程式で解きたいですね。。 y = x2 …① y= x+6 …② ①,②より x2=x+6 両辺に−をかけて、 x2−x−6=0 (x−3)(x+2)=0 x=3,−2 x軸と3と−2で接することが分かりました。 x=3のとき、①式(②式に代入しても可) y=−9 x=−2のとき y=−4 よって、求める座標は A(3,−9),B(−2,−4) |
 |
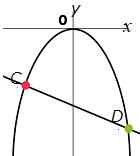
| 例2 右のグラフはy=−x2 のグラフとy= −x−6の直線です。 交点の座標CとDを求めてみよう。 これも連立方程式で解きたいですね。 y=−x2 …① y= −x−6 …② ①,②より −x2=−x−6 両辺に−をかけて、 x2=x+6 x2−x−6=0 (x−3)(x+2)=0 x=3,−2 x軸と3と−2で接することが分かりました。 x=3のとき、①式(②式に代入しても可) y=−9 x=−2のとき y=−4 よって、求める座標は A(3,−9),B(−2,−4) |
 |
| 問1 放物線y=−x2 上に2点A,Bがある。点Aと点Bのx座標はそれぞれ−3と2である。 ① 点A,点Bの座標をそれぞれ求めなさい。 ② 直線ABの式を求めなさい。 ③△OABの面積を求めなさい。 |
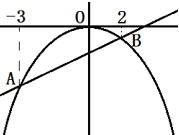 |
解説
① 点A,点Bの座標は y=−x2 の式から
x=2のとき, y=−4
x=-3のとき, y=−9 点Aの座標(-3,-9)点Bの座標(2,-4)
② 直線ABの式は y=ax+b から
-9=-3a+b …①
-4= 2a+b …② 連立方程式を解くと①−②
-5=-5a a=1 aを①式に代入して b=-6
よって、求める式は y=x-6
③ 直線ABとy軸の交わる点を仮にCとおくと、△OABの面積は
△OAB=△OCA+△OCB 底辺はOC=6で
△OCAの面積=(6×3)÷2=9
△OCBの面積=(6×2)÷2=6 よって、△OABの面積=15
グラフ原本