①
⑤
⑨
| 1章 正の数・負の数 ・正の数・負の数 ・加法と減法 ・乗法と除法 ・四則をふくむ式の計算 |
5章 平面図形 ・図形の基礎 ・対称な図形 ・基本の作図 ・おうぎ形 |
| 2章 文字と式 ・文字を使った式 ・1次式の計算 |
6章 空間図形 ・いろいろな立体 ・直線や平面の位置関係 ・立体の構成 ・立体の表面積と体積 |
| 3章 方程式 ・1次方程式 ・1次方程式の利用 |
|
| 4章 比例と反比例 ・比例 座標, ・比例のグラフ ・反比例とグラフ ・比例と反比例の利用 |
7章 資料(データ)の活用 |
1章 正の数・負の数
加法と減法
| 問1 次の計算をしなさい。 ①(-13) + 9 = ②(-5)- 4 = ③5-(-3)-(+1) = ④ 1.9-(-0.7) = ⑤9-(-3)-10 = |
|
問2 次の計算をしなさい。 |
答 ① +6 ② -8 ③ -9 ④ -1 ⑤ +9 ⑥ -49
⑦ +7 ⑧ +90 ⑨ -2 ⑩ +2 ⑪ -4 ⑫+13
⑬+5.7 ⑭-1.4 ⑮-5.4 ⑯+1.7 ⑰-1.6
⑱+3.5 ⑲-5 ⑳-39
乗法と除法 四則をふくむ式の計算
| 問1 次の計算をしなさい。 ① 12+(-5)×3 = ② 2×(-4)+10 = ③ 9+3×(-2) = ④ 8+(-3)× 2 = ⑤ (-2)×4 + 9 = ⑥ 7+(-4)×2 = ⑦ (-2)×3 + 5 = ⑧ (-2)×(-3)-5 = |
| 問2 次の計算をしなさい。 ① ⑤ ⑨ |
| 問3 以下の式を解きなさい ① 3(a-1)-2(a+3)= ② 3(a+2)-(a-1)= ③ 5(a+1)-(a+4) = ④2(a+3)-(a-1)= ⑤ 4(x-1)-(x+3)= ⑥ 3(b+5)-(b-2) = ⑦ 2(y-1)-(3y-4)= ⑧ 2(3x-1)-(x-4)= |
■絶対値
| 問1 (1)正の整数のことを何と呼ぶか。 (2)正の数でも負の数でもない数を答えよ。 (3)自然数に0は入るか (4)絶対値とは何か。 (5)負の数では、絶対値が大きいものと絶対値が小さいものどちらの数が大きい数になるか。 |
答 (1)自然数 (2)0 (3)0は自然数に入らない
(4)数直線上で原点からの距離 (5)絶対値が小さいほうが大きい数になる。
| 問2 次の数の絶対値を答えなさい。 ① -4.5 ② +6.4 ③ -29 ④ 0 |
①4.5 ②6.4 ③29 ④0
| 問3 (1)絶対値が3以下の整数をすべて答えよ。 (2)絶対値が2以上5以下の整数をすべて答えよ。 (3)2つの数がある。この2つの数の絶対値は等しく、この2つの数の差は17である。 この2つの数を求めよ. |
答 (1) –3, -2, -1, 0, +1, +2, +3 ※ +1, +2,を1, 2のように、一般的に数学では+を省略します。
(2) –5, -4, -3, -2, +2, +3, +4, +5 (3) -8.5 と+8.5
| 問4 次の各組の数の大小を不等号を使って表しなさい。 ① +0.2, -3 ② -120, +0.5 ③ -1.2, -1.4 ④ -0.01, -1.1 ⑤ -5.02, -4.95 ⑥ -0.01, -0.001 |
答
①+0.2 > -3 ②-120 < +0.5 ③-1.2 > -1.4
④-0.01 > -1.1 ⑤-5.02 < -4.95 ⑥-0.01 < -0.001
■近似値 有効数字
サミングアップ p66
| 問1 ある数aの十の位を四捨五入すると 2700になった 誤差の絶対値は最大でいくつですか |
解答
2700は、2650から、2749 (2700-2650)=50で 50 …答
| 問2 ある数bの小数第2位を四捨五入すると5.0になった。bの範囲を不等号を用いて表せ。 |
答 4.95≦b<5.05
4.94では小数第2位を四捨五入すると4.9になります。4.95なら5.0 よってbは4.95以上
反対に5.05では小数第2位を四捨五入すると5.1になります。
| 問 地球の直径12800kmをmを単位としてあらわすと1.28×10nである。nの値は |
解答
まず12800kmは1.28×10000㎞ → 1.28×104km
1.28×104km をメートルに直すと、(1.28×104)×103 m
よって1.28×107 n=7
■比例と反比例 座標
問 以下の座標を右の表に書き入れなさい。 A(1,2) B(2,2) C(3,3) D(−2,2) E(−3,−3) |
 |
| 答 右の図 A(1,2) B(2,2) C(3,3) D(−2,2) E(−3,−3) |
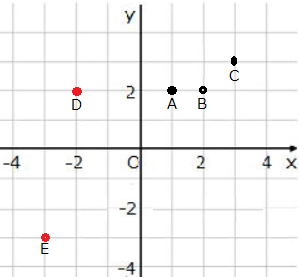 |
(1)比例
「変化の割合」とは、ある関数についてxが「変化」したときに、
![]() がどれくらい「変化」するかを割り算で表したもの(割合)になります
がどれくらい「変化」するかを割り算で表したもの(割合)になります
![]() の値が2倍、3倍・・・になると、
の値が2倍、3倍・・・になると、![]() の値が2倍、3倍・・・になる。
の値が2倍、3倍・・・になる。
このとき、yは xに比例するといいいます。
比例の式 y=ax
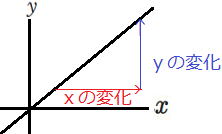
以下の図のように、比例定数aが正(+)か負(-)によって傾きが右上がりか、右下がりの直線になります。
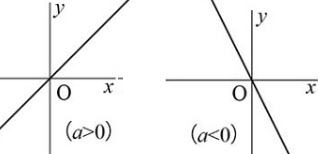 左の図のように直線になります。
左の図のように直線になります。
式は y = a x a:傾き(比例定数) 直線は原点Oで接します。
下のグラフは y=2x (傾きが2)の例
y=2x
|
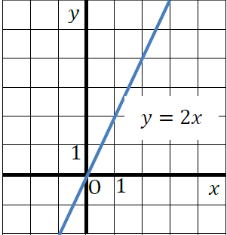 |
| 問1 次の式のグラフを書きなさい |
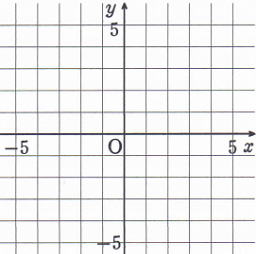 |
答
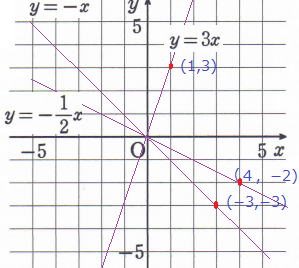
| 問2 yはxに比例し、xとyが次の値をとるとき、yを xの式で表しなさい。 (1) x =−2のとき y =2 (2) x=−4のときy =2 (3) x=9のときy=−1 (4) x =5のときy =−3 |
(2) 反比例
(1) 下のグラフは反比例のグラフ。 ![]() で表します。
で表します。
具体的に反比例について考えてみましょう。
| 縦 acm 横 bcm、面積12㎠の長方形です。次の式は何を表しているでしょうか。p8 (1) ab (2) a+b |
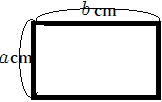 |
(たての長さ)×(横の長さ)=(長方形の面積)ですね。
縦の長さ a ㎝、横の長さ b ㎝の長方形の面積が12㎠。
以下の公式が成り立ちます。 ab = 12 abは a×b で、一般的に数学では×は省略します。
面積が12㎠と固定されてますので、
縦の長さ aが長くなると、横の長さ bは短くなりますね。
横の長さ b が長くなると、縦の長さ aは短くなり、aとbは反比例の関係にあります。
以下、ab= 12を xy =12に置きかえ、グラフについて考えてみましょう。
xy =12 は yについて整理すると ![]() ですね。
ですね。
グラフを書くまえに、![]() の値を埋めてみましょう
の値を埋めてみましょう

以下は(反比例)![]() のグラフです
のグラフです
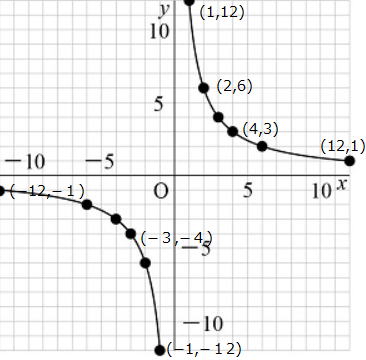
・比例定数a >0 と a< 0の場合のグラフ(下図)
双曲線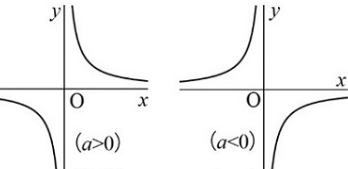
問1 次の式のグラフを書きなさい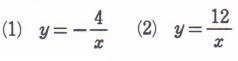 |
 |
答
| 問2 yはxに反比例し、 x=−3のとき y =4です。 (1) yをxの式で表しなさい。 (2) x =4のときの yの値は。 (3) x=−16のとき、yの値は。 |
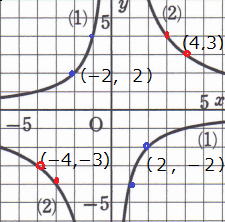
| 問3 右の双曲線は反比例のグラフです。 (1) 点Aの座標は? (2) このグラフについて、yをxの式で表しなさい。 |
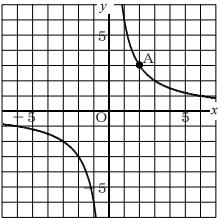 |
|
問4 下のア~エまでのグラフで①
|
| 右のヒストグラムは、あるクラスの男子の身長の記録である。 (1) 人数の合計を求めよ。 (2) 160㎝以上165㎝未満の生徒の相対度数を求めよ。 (3) 165㎝以上の生徒の相対度数を求めよ。 (4) それでは25人のクラスで、170以上の生徒の相対度数が0.2のとき、 その人数を求めよ。 sumより |
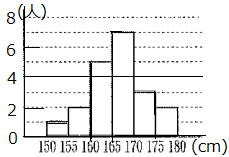 |
答
(1) 20人 (2) 0.25 (全体で20人 160㎝以上165㎝未満の生徒数は5人)
相対度数は1以下
| 右の表は40人の生徒の体重をはかり、度数分布表に整理したものである。次の問いに答えなさい。 (1) ① 45㎏~50㎏ ② 60㎏~65㎏ の階級について 相対度数を求めなさい。 (2) 度数分布表を完成させなさい。 (3) 度数分布表をもとに、生徒の体重の平均値を求めなさい。 |
|
答 (1) ①0.4 ②0.05 (2) (3)50㎏
| 体重(㎏) | 階級値(㎏) | 度数(人) | 階級値×度数 |
| 以上 未満 40~45 |
42.5 | 6 | 42.5×6=255 |
| 45~50 | 47.5 | 16 | 47.5×16=760 |
| 50~55 | 52.5 | 12 | 52.5×12=630 |
| 55~60 | 57.5 | 4 | 57.5×4=230 |
| 60~65 | 62.5 | 2 | 62.5×2=125 |
| 計 | 40 | 2000 |
| 問15 右の表は40人の生徒の体重をはかり、度数分布表に整理したものである。次の問いに答えなさい (1) ①45㎏~50㎏ ②60㎏~65㎏の階級について、相対度数を求めなさい。 (2) 度数分布表を完成させなさい。 (3) 度数分布表をもとに、生徒の体重の平均値を求めなさい。 |
|
答 (1) ①0.4 16/40=2/5=0.4 ②0.05 2/40=0.05 (2)下図 (3)50㎏
| 体重㎏ | 階級値(㎏) | 度数(人) | 階級値×度数 |
| 以上 未満 40~45 | 42.5 | 6 | 42.5×6=255 |
| 45~50 | 47.5 | 16 | 47.5×16=760 |
| 50~55 | 52.5 | 12 | 52.5×12=630 |
| 55㎏~60 | 57.5 | 4 | 57.5×4=230 |
| 60~65 | 62.5 | 2 | 62.5×2=125 |
| 計 | 40 | 2000 |
相対度数
| 問1 右の表は、あるクラスで1日のテレビの視聴時間を調べた記録である。 空欄( |
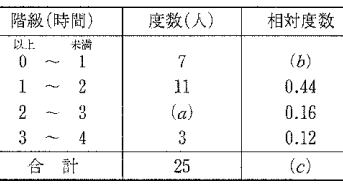 |
答 (![]() ) 25-(7+11+3)=4
) 25-(7+11+3)=4
(![]() ) 7÷25=0.28 相対度数は各階級の度数を相対度数の合計で割った値です。
) 7÷25=0.28 相対度数は各階級の度数を相対度数の合計で割った値です。
(![]() )1.00 相対度数の合計は1.00(100%)
)1.00 相対度数の合計は1.00(100%)
p66
| 問16 右のヒストグラムはあるクラスの身長の記録である。 ①身長の高い方から数えて10番目の生徒はどの階級に入るか。 ②140㎝以上170㎝未満の生徒の割合は何%か。 | 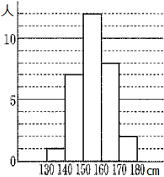 |
答
① 160㎝以上170㎝未満 8+2=10(人)
② 90% 140㎝以上170㎝未満の生徒数は7+12+8=27
クラス全体の数 1+7+12+8+2=30人なので (27/30)×100 = 90%
代表値・平均
p66
| 問17 右の表はAさんが25日間のバスの待ち時間を調べた結果である。 次の問いに答えよ。 ① 右表の□を埋めよ。 ② 最頻値を答えよ。 ③ 待ち時間の平均を求めよ。 | 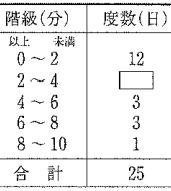 |
答 ① 6 ② 1分 ③ 3分
階級値はそれぞれ1、3、5、7、9 度数はそれぞれ12、6、3、3、1 度数の合計は25日
(1×12)+(3×6)+(5×3)+(7×3)+(9×1)=12+18+15+21+9=75 75÷25=3
p67
| 問18 右のヒストグラムで、①,②,③はそれぞれ中央値、最頻値、平均値のどれか、答えなさい。 ① ② ③ |
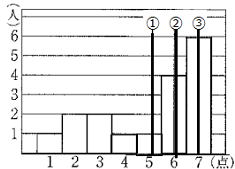 |
答 ①平均値 ②中央値 ③最頻値

1 4 6 4 5 24 42 合計86点 17人 平均値 86÷17=5.05
中央値は順位が中央の値 最頻値は度数が一番多い値
以上
---------------------------------------
中1復習問題
| 中1復習問題 その1 問1 次の計算をしなさい。p8 ① -9+(-1) ②-9-(-1) ③-9×(-1) ④-9÷(-3) ⑤ 6x+ 3-x-1 ⑥ -7x+16x ⑦ 4×(-6x) ⑧-5x×8 ⑨ −17x+2x ⑩ -17x-2x ⑪ −3a+2a ⑫ a-(a-1) |
| 問2 次の計算をしなさい。 ① 4×(-6) + 21 ②-5×8+31 ③ -17-2×(-4) ④ -11+ 3×(-6) ⑤ -7 + 16 ÷(-2) ⑥(-36)÷ 4 + 11 ⑦ -5-(-42)÷ 7 ⑧ (-27)÷(-3)-(-8) |
答
①4×(-6)+ 21 = -3 ②-5×8+ 31= -9 ③-17-2×(-4)= -9 ④-11+ 3×(-6)=-29
⑤-7+16÷(-2)=-15 ⑥(-36)÷4+11= 2 ⑦-5-(-42)÷7= 1 ⑧(-27)÷(-3)-(-8)= 17
| 問3 1.次の方程式を解きなさい。 2. (1) x:6=5:3 (2) 3:2=x:5
問5 次の問いに答えなさい。  |
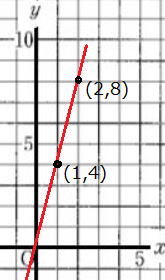
| 答 3. (1) y = ax とおく.。 20=5a よってa =4 y=4x…答 (2) x=-2 をy= 4xに代入 y=-8 …答 (3) y=4xの傾きは4、原点を通る直線(右図) 4.こうした問いは簡単な絵を描くことです。 ① xにyをかけたら距離18㎞ x×y=18より y=18/x ② 上の式は反比例の式 ③ 比例定数は18 |
 |
--------------------------------------------------
| 問6 次の式のグラフを書きなさい。 |
 |
答

問7 次の式のグラフを書きなさい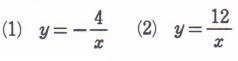 |
 |
答

| 問8 yはxに反比例し、xとyが次の値をとるとき、yをxの式で表しなさい。 (1) x=−2のときy=2 (2) x=−4のときy=2 (3) x=9のときy=−1 (4) x=5のときy=−3 |
| 問9 yはxに反比例し、x=−3のときy=4です。 (1) yをxの式で表しなさい。 (2) x=4のときのyの値は。 (3) x=−16のとき、yの値は。 |
| 問10 右の双曲線は反比例のグラフです。 (1) 点Aの座標は (2) このグラフについて、yをxの式で表しなさい。 |
 |
|
問11 下のア~エまでのグラフで①
|
体積の問題を求めるまえに、面積の問題をやってみよう‼
| 問1 以下の影部分の面積を求めなさい。また、①の問いの円周を求めなさい。 ① 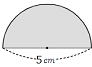 ② ②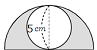 ③ ③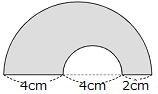 ⓸ ⓸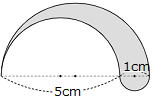 |
答 ① ㎠ ② ㎠ ③ ㎠ ④ ㎠ ①の円周 ㎝
| 問2 (1) 半径がrのときの円の周の長さと面積を答えなさい。 (2) 半径がr、高さをhとするとき、円柱と三角錐の体積を答えなさい。 (3) 半径が5㎝、高さが9㎝のとき、それぞれ円柱と三角錐の体積を求めなさい。 |
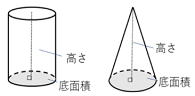 |
(1) 周の長さ: 2πr 面積:πr2 (2)円柱の体積:πr2h 三角錐:1/3(πr2h)
(3) 円柱の体積:225π㎤ 三角錐:75π㎤
※ 円錐、三角錐、四角錘……n角錘の体積は、それぞれ円柱、三角柱、四角柱……n角柱の1/3です。
| 問3 右の図の円錐について,次の問いに答えなさい。 (1) 底面の円の面積(底面積)と周の長さを求めなさい。 底面積: 周の長さ: (2) 側面のおうぎ形の中心角を求めなさい。 (3) この円錐の表面積を求めなさい |
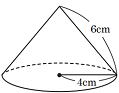 |
(1) 底面の円の面積(底面積)と周の長さ
底面積 16πcm2 周の長さ 8πcm …答
(2) 側面のおうぎ形の中心角
底面の円の周の長さと,側面のおうぎ形の弧の長さは等しいので,
おうぎ形の中心角を仮にa� とおきます。 240°…答
(3) この円錐の表面積
表面積は,16π+ 24π = 40π 40π cm2…答
■球の体積
![]() ☜ 覚えること
☜ 覚えること