（展開 因数分解 方程式）展開の復習問題
総合問題 戻る
以下の①～④までが公式です。
（展開 因数分解 方程式）
展開の復習問題
総合問題 戻る
以下の①～④までが公式です。
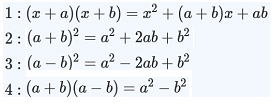
次の式を乗法の公式①を使って、展開してみよう。
| 例 (1) (x＋3)(x−2)= (2) (x＋3)(x＋2)= (3) (x＋2)(x＋1)= (4) (x＋1)(x−2)= (5) (x−2)(x＋1)= (6) (y＋2)(y−2)= |
答
(1) (x＋3)(x−2)=x2＋x−6 (2) (x＋3)(x＋2)=x2＋５x＋６
(3) (x＋2)(x＋1)=x2＋x−2 (4) (x＋1)(x−2)=x2－x−2
(5) (x−2)(x＋1)=x2－x−2 (6) (y＋2)(y−2)=y2−y−２
少し、難しいかもしれませんが、頑張ってみよう！。
| 問 次の式を展開せよ ①(x＋2)(x−2) ②(2x＋2)(x−3) ③(x＋2)(3x−8) ④(3x＋2)(3x−2) ⑤(x＋2y)(x−3y) ⑥ (x−2y)(x−3y) ⑦(x−6y)(x−8y) ⑧(3x+10)(x−3y) ⑨(3a+6b)(5a−9b) |
▲公式②、③
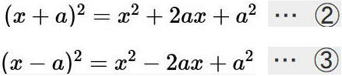
| 例 (x−５)2 を展開してみよう。
xと(−５)を掛けて５x。５xを２倍にします。 |
実際にやってみましょう。
| 問 次の式を展開しなさい。 ① (x+５)2 ② (x−１)2 ③ (x−５)2 ④ (x＋５y)2 ⑤ (x−y)2 ⑥ (x−５y)2 ⑦ (２x+５)2 ⑧ (２x−１)2 ⑨ (3x−５)2 ⑦ (２x+５y)2 ⑧ (２x−y)2 ⑨ (5a−6b)2 |
 |
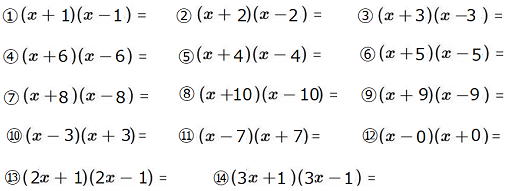※「乗法の公式を使わなくても良いじゃあないか。せっかく分配の法則を勉強したし…」
ってと思う生徒さんもおられるでしょう。
でも、何度もしつこいようですが、 この公式は便利なうえ、非常に大切なんです。
高校に進学してからも、よく使います。
できるできないの違いは「頭の良し悪し」じゃありません、
数多くの問題にチャレンジするかしないかの違いです
| 問 次の式を展開しなさい ① (x＋1)(x＋2) ② (x＋1)(x−2) ③ (x−1)(x−2) ④ (  ＋1)2 ⑤ (＋1)(−2) ⑥(−3)(＋1) ⑦( −1)2 ⑧ (＋1)(−2) ⑨ (−2)2 ⑩ ( ＋2)(−2) ⑪(＋1)(＋2) ⑫ (＋2)2⑬ ( ＋3)(−3) ⑭ (＋5)(＋3) ⑮ (＋5)(−5) |
因数とは… (＋3)(−2)の式で
(＋3)や(−2)など、それぞれを因数といいます。
図１は展開、下の図２は因数に分解する公式です。
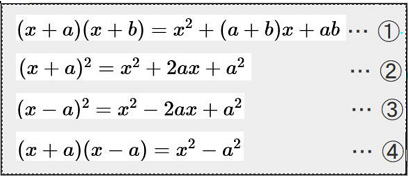図１ 
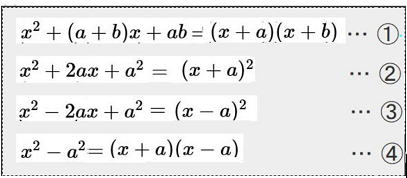図２
上の図1は、乗法の公式で最初にみた公式ですね。
右図は左辺と右辺を逆にした公式です。下図のように、
因数分解とは、それこそ因数に分解（整理）することです。
因数分解の反対が展開、展開の反対が因数分解と考えていいでしょう。
難しい説明はさておいて、実際の問題で理解しましょう。
| 例 以下は公式①を使った例題です。解いてみよう。 ① x²＋４x−12= ② x²+ ３x＋２= ③ x²＋x −2= ④ x²+４x ＋３= ⑤ x²+２x−３= ⑥ x²−２x−３= |
公式①から④までの総合問題 (因数分解)
因数分解 乗法の公式①～④を使って因数分解してみよう
ただし問１の問題は乗法の公式は使いません。
| 問１ 因数分解しなさい。 ①  ② ③ ④ ⑤  ⑥ ⑦  ⑧ |
| 問２ 因数分解しなさい。 ①  ② ③ ④ ⑤  ⑥ ⑦ ⑧ ⑨  ⑩ ⑪ ⑫ ⑬  ⑮ ⑯ ⑰ ⑱  ⑲ ⑳ |
| 問３ 因数分解しなさい。 ①  ② ③ ④ ⑤  ⑥ ⑦ ⑧ ⑨ ⑩  ⑪ ⑫ ⑬ |
因数分解ができたら、方程式は簡単‼
例えば上の問題④の答えは 
+－６ =(+３)(+２)ですね。
④は因数に分解したので、これが方程式になると、
「
+－６ =０の２次方程式を解け」 のような問いになります。
＋－６ = ０ は （+３)(－２)=０ に因数分解できるね。
（+３)=０ （－２)=０ それぞれの因数から = －３と =２ ＝－３ , ２…答
それでは実際に２次方程式を解いてみよう。
| 問 次の２次方程式を解きなさい ① =０ ②=０ ③=０ ④=０⑤ =０ ⑥=０ ⑦=０ ⑧=０⑨ =０ ⑩=０ ⑪=０ ⑫=０⑬ =０ ⑭ =０ ⑮=０ ⑯=０⑰ =０ ⑱=０ ⑲=０ ⑳=０ |
解説）①を解いてみましょう。中学で学習する方程式は１次方程式と２次方程式がありますが、
中3では２次方程式を学びます。
+８+７ = ０ まず左辺を因数分解します。
+８+７ = ０ （+１)(+７)=０
（+１)=０と (+７)=０の場合が考えられますね。
まず（+１)=０のとき、 +１=０からを求めるには１を右辺に移項します。よって=－１
同様に （+７）=０ =－７ =－１，－７ …答
■総合問題 展開 ⇆ 因数分解 方程式
| 問１ 式を展開しなさい ① (x＋１)2 ② (x＋２)2 ③ (x＋２)(x−１) ④ (x＋３)(x−２) |
答 そのまま、問２の式になります。 例 ①x2＋2x＋１ ② x2＋４x＋４
| 問２ 因数分解しなさい ① x2＋2x＋１ = ② x2＋４x＋４ = ③ x2＋x−２ = ④ x2＋x−６ = ⑤ x2−４x＋４ = ⑥ x2−２x＋１ = ⑦ x2−x−２ = ⑧ x2＋６x＋９ = ⑨ x2−６x＋９ = ⑩ x2−４ = ⑪ x2＋10x＋25 = ⑫ x2−10x＋25 = ⑬ x2 −１６ = ⑭ x2＋８x＋16 = ⑮ x2−８x＋１６ = ⑯ x2−５x＋６ = ⑰ x2−x−６ = ⑱ x2＋12x＋36 = ⑲ x2−12x＋36 = ⑳ x2 − 25 = |
答
① x2＋2x＋１ = (x＋１)2 ② x2＋４x＋４ = (x＋２)2 ③ x2＋x−２ = (x＋２)(x−１)
④ x2＋x−６ =(x＋３)(x−２) ⑤ x2−４x＋４ = (x−２)2 ⑥ x2−２x＋１ = (x−１)2
⑦ x2−x−２ = (x＋１)(x−２) ⑧ x2＋６x＋９ = (x＋３)2 ⑨ x2−６x＋９ = (x−３)2
⑩ x2 −４ = (x＋２)(x−２) ⑪ x2＋10x＋25 = (x＋５)2 ⑫ x2−10x＋25 = (x−５)2
⑬ x2 −16 = (x＋４)(x−４) ⑭ x2＋８x＋16 = (x＋４)2 ⑮ x2−８x＋１６ = (x−４)2
⑯ x2−５x＋６ =(x−３)(x−２) ⑰ x2－xー６ =(x−３)(x＋２) ⑱ x2＋12x＋36 = (x＋６)2
⑲ x2－12x＋36 = (x−６)2 ⑳ x2 − 25 = (x＋５)(x−５)
|
問３ 因数分解しなさい ① |
| 問４ 次の方程式を解きなさい ① m2＋2m＋１ =０ ② 4m2＋４m＋1 =０ ③ m2＋m−２ =０ ④ a2＋a−６＝０ ⑤ n2−４n＋４ =０ ⑥ 4m2−4m＋１ =０ ⑦ a2−a−２ =０ ⑧ a2＋26a＋169 =０ ⑨ 25a2−10a＋1 = ０ ⑩ 25x2 −４ =０ ⑪ x2＋22x＋121 =０ ⑫ a2−26a＋169 =０ ⑬ 9m2 −１６=０ ⑭ 9m2＋1８m＋1 =０ ⑮ 9m2−24m＋16=０ ⑯ x2−５xy＋６y2 =０ ⑰ x2−xy−６y2 =０ ⑱ x2＋12xy＋36y2 =０ ⑲ x2−12xy＋36y2 =０ ⑳ x2−169y2 =０ |
乗法の公式①～④を使って因数分解してみよう
| 問１ー１ 次の式を展開しなさい ① (2x＋１)2 ② (3x＋２y)2 ③ (3x＋２)(2x−１) ④ (x＋３)(x−２) |
| 問１−２ 次の式を展開しなさい。 注意 (1)から(4)は乗法の公式は使えません。 ① (a＋2)(b＋2) ② (a＋4)(b＋7) ③ (a＋3)(b−3) ④ (x−2)(y−4) ⑤ (a＋3)(a＋2) ⑥ (a−4)(a−7) |
| 問２ 次の式を因数分解しなさい。 ① ② ③ ④⑤ ⑥ ⑦ ⑧ |
| 問３ 次の式を因数分解しなさい。 ① 4x2＋8x−5 ② 4x2−20x＋25 ③ x2＋x−２ ④ 25x2＋5x−6 ⑤ x2−22x＋121 ⑥ 9x2−6x＋１ ⑦ x2−x−２ ⑧ x2−24x＋144 ⑨ x2−10x＋９ ⑩ 25x2 −４ ⑪ 9x2＋30x＋25 ⑫ x2−10x＋25 ⑬ 9x2 −16 ⑭ x2＋17x＋16 ⑮ 9x2−24x＋16 ⑯ x2−21x＋110 ⑰ x2－x－６ ⑱ x2＋12x＋36 ⑲ 4x2−24x＋36 ⑳ 4x2−25 |
| 問４ 次の方程式を解きなさい。 ① 4x2＋8x−5 =０ ② 4x2−20x＋25=０ ③ x2＋x−２ =０ ④ 25x2＋5x−6 =０ ⑤ x2−22x＋121 =０ ⑥ 9x2−6x＋１ =０ ⑦ x2−x−２ =０ ⑧ x2−24x＋144 =０ ⑨ x2−10x＋９ =０ ⑩ 25x2 −４ =０ ⑪ 9x2＋30x＋25 =０ ⑫ x2−10x＋25 =０ ⑬ 9x2 −16 =０ ⑭ x2＋17x＋16 =０ ⑮ 9x2−24x＋16 =０ ⑯ x2−21x＋110 =０ ⑰ x2－x－６ =０ ⑱ x2＋12x＋36 =０ ⑲ 4x2−24x＋36 =０ ⑳ 4x2−25＝０ |
② 
③ 
④ 