中学2年数学 
目次 戻る
challenge
中1の教科書に出題されてました。
頭を抱えている生徒さんが多かったので、以下に挙げます。
63をできるだけ小さい自然数で割って、ある自然数の2乗にするには
どのような数で割ればいいですか? |
解 63を素因数分解すると63= 3²×7なので、
3²×7² 7…ans
似た問いをもう一題
540をできるだけ小さい自然数で割って、ある自然数の2乗にするには
どのような数で割ればいいですか? |
解 540=2²×3³×5 3×5=15…ans
|
 中2サミングアップ 問題
中2サミングアップ 問題  中1の復習問題
中1の復習問題
1 式の計算
| 問 次の式を解きなさい。
① (-3)2 ② -42 ③ 10-(-3)2 ④ 12+(-42)
|
答 ① (-3)2=9 ② -42= -16 ③ 10-(-3)2=1 ④ 12+(-42)=-4
問1 次の等式を,[ ]内の文字について解きなさい。
(1) xーy =10 [x] (2) S = ab [a] (3)ℓ= 2πr [r]
(4) x=50-2y [y] (5) 6x+2y = 1 [x]
|
答 (1)x=y+10 (2) a=S/b (3) r=ℓ/2π (4) y= 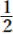 x+ 25 (5)y=-3x+
x+ 25 (5)y=-3x+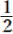
問2 ( )内の文字について解け
(1) x-7y+1=0 [x] (2) x+3 y-1=0 [x] (3)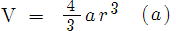
|
答 (1) x=7y-1 (2) x=-3 y+1 (3) 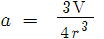
問3 a=-2,b=3のとき、以下の式の値を求めよ。
① 4a-5b-(a-4b)
② 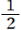 ab ③ ab ③ 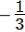 (a+b) (a+b) |
まず、与えられた式を、展開し、まとめてからa、bの値を代入しよう‼
① 4a-5b-(a-4b)=4a-a-5b+4b=3a-b
3a-b に a=-2,b=3の値を代入します。
3(-2)-3=-6-3=-9 …答
② S = -3
問4 a=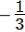 ,b= ,b=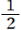 のとき、ab-2aの値を求めよ。 のとき、ab-2aの値を求めよ。 |
この問題も同じように、与えられた式を展開し、式をまとめてからa、bの値を代入しよう‼
2節 文字式の利用
問1
(1)右のカレンダーにおいて、5つの数を で囲んだとき,囲まれた5つの数の和は5の倍数になっている。このことがカレンダーのほかの5つの数でも成り立つわけを説明しなさい。 で囲んだとき,囲まれた5つの数の和は5の倍数になっている。このことがカレンダーのほかの5つの数でも成り立つわけを説明しなさい。
(入試に頻繁に出題される問題です)
|
 |
解答 中央の整数をnとすると、左の数はn-1,右の数はn+1,上の数はn-7、下の数はn+7と表せる。
5つの数の和はn+(n-1)+(n+1)+(n-7)+(n+7)=5n
nは整数なのでnは5の倍数である。
問2 百の位の数が一の位の数より大きい3けたの自然数から、その数の百の位の数と一の位の数を入れかえてできる数を引くと、その差は99の倍数になることを次のように説明した。( )にあてはまる文字式を入れなさい。
もとの3けたの自然数の百の位の数をx、十の位の数をy、一の位の数をzとし、xはzより大きいものとすると、もとの数は( ① )と表せる。
入れかえてできる数は( ② )となるので、その差は
( ① )−( ② )= 99 x−99 Z=99 ( ③ )
( ③ )は整数だから、99 ( ③ )は99の倍数である。
|
■連立方程式
 数学は皆さんを苦しめるためにあるのではありません。
数学は皆さんを苦しめるためにあるのではありません。
わたしたちが楽するためにあるのです。
例えば小学校で習った「つるかめ算」を解いてみましょう。
| つるとかめの頭の数が合計50で、足の数が合計156本の時、つるとかめはそれぞれいくつですか? |
【手順1】 つる足の数は2本、かめ足の数は4本。
【手順2】 頭の数の合計50が全てつるだったとします。
このとき、足の数の合計は 2×50=100(本) となり、実際の足の数156本より
156-100=56(本)たりません。
【手順3】つる1羽をかめ1匹に置きかえる。
足の数は、4-2=2(本)増えます。
【手順4】足の数を56本増やしてかめの数を求める。
足の数を56本を増やすと合計156本になるので、つるをかめに置きかえる数は、
56÷2=28(匹) かめの数です。 よって、つるの数は 50-28=22(羽)
ややこしいし、時間がかかります。これを連立方程式で計算してみましょう。
かめの数をx匹、つるの数をy羽とおきます。
x+y=50 …① 4x+2y=156 より 2x+y=178…②
①と②の式から、簡単に x=28, y=22 かめの数:28匹 つるの数:22羽
問1 次の連立方程式を解きなさい。 p22
①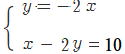 ② ②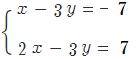 ③ ③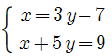
④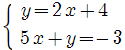 ⑤ ⑤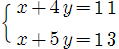 ⑥ ⑥ 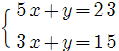
⑦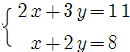 ⑧ ⑧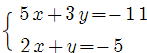
|
解説
①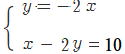 y =-2xをそのまま、下の式に代入するのが楽でしょう。
y =-2xをそのまま、下の式に代入するのが楽でしょう。
x- 2(-2x) = 10 x+ 4x =10 5x =10 x =2
x =2 を y =-2xに代入して y=-4 x =2,y=-4 (答)
② 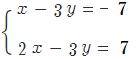 上の式から下の式を引くと y が消えますね。
上の式から下の式を引くと y が消えますね。
-x =-14 x=14 上の式に代入して、-3 y =-21 y = 7
x =14,y=7 (答)
③、④も①の問いと同じやり方が楽ですね。
x= 3y−7 …①
x+5y = 9 …② ①式を②式に代入すると、3y−7+5y=9
よって、 8y=16 y=2 これを①式に代入すると、x=-11
x =-11 , y =2 …答
④ x =-1 , y =2 …答
⑤ ②と同じように、上の式から下の式を引くと楽に解けます。
解き方は人によって違いますが、できるだけ、式の形から楽な解き方を見つけてください。
x =3 , y =2 …答
⑥ x =4 , y =3 …答 ⑦ x =-2 , y =5 …答 ⑧ x =-4 , y =3 …答
問2 次の連立方程式を解きなさい。
(1) 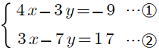 (2) (2) 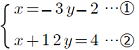 |
答 (1) x=-6 , y=-5 (2) 
(1) ①×3 ②×4倍して xを 12xにして消去するといいね。
①×7 ②×3 して yを 21y にして yを消去する方法もあるね。
■連立方程式の利用(文章題)
連立方程式を使わなかったら大変だね。楽するのが数学です。問4は、たびたび入試に出題される問題です。
問1 A,Bの2人がバスケットボールのシュートの練習で,1本入ると2点,はずすと0点とするゲームを行った。入ったシュートの本数はAがBより3本多く,2人の得点の合計は18点だった。入ったシュートの本数をAが x本、Bが y本として次の問いに答えなさい。
(1) 入ったシュートの本数の関係について方程式をつくりなさい。
(2) 得点の関係について方程式をつくりなさい。
(3) A,Bの入ったシュートの本数を、それぞれ求めなさい。
問2 ある博覧会の入場料は,子ども4人とおとな1人で3,800円,子ども2人とおとな2人の入場料は3,400円である。子ども1人とおとな1人の入場料をそれぞれ求めなさい。
問3 1個200円のケーキと1個120円のプリンをあわせて10個買い,1,500円出したら,おつりが60円あった。買ったケーキとプリンの個数を、それぞれ求めなさい。
問4 360m離れたところまで行くのに、途中までは分速60m、途中から分速80mで行き,全体で5分で行くことにしたい。分速60mで行く道のりをxm、分速80mで行く道のりをymとして次の問いに答えなさい。
(1) 道のりの関係について方程式をつくりなさい。
(2) 時間の関係について方程式をつくりなさい。
(3) 分速60mで行く道のりと分速80mで行く道のりを、それぞれ求めなさい。
|
答 問1 (1) x-y=3…① (2) 2x+2y=18 x+y=9…②
(3) ①,②より x=6,y=3 Aさん 6本 / Bさん 3本
問2 子ども1人の入場料をx円 おとな1人の入場料を y 円とおく
4x+y=3800…① 2x+2y=3400は x+y=1700…② ①,②より
x=700, y=1000 こども:700円 おとな:1000円
問3 ケーキ 3個 プリン 7個
問4 (1) x+ y = 360 (2) x/60+y/80=5
(3) 分速60m:120m 分速80m:240m
| 問5 2けたの正の整数がある。その整数は,各位の数の和の4倍よりも3大きく,十の位の数と一の位の数を入れかえてできる2けたの数は,もとの整数よりも36大きくなる。もとの整数を求めなさい。(入試に頻繁に出題される問題です) |
答 59 以下の方程式が成り立つ。
10x+y=4(x+y)+3 …①
10y+x=10x+y +36…② x=5, y=9

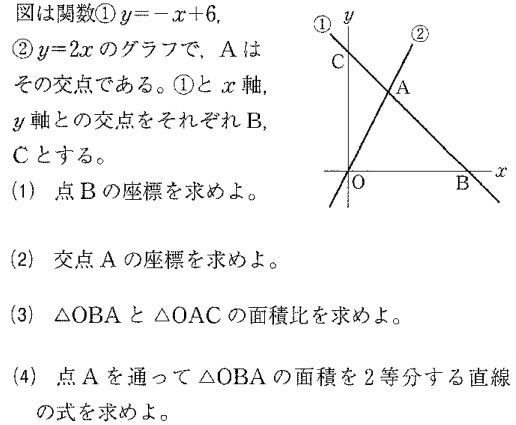
(3) 一次関数のグラフ
(ここでは、1年で学習した比例のグラフをyに平行移動したグラフを学びます)
■座標
【復習】
問1 以下の座標を右の表に書き入れなさい。
A(1,2) B(2,2) C(3,3)
D(−2,2) E(−3,−3) |
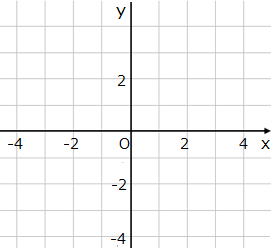 |
答 右の図
A(1,2) B(2,2)
C(3,3) D(−2,2)
E(−3,−3)
|
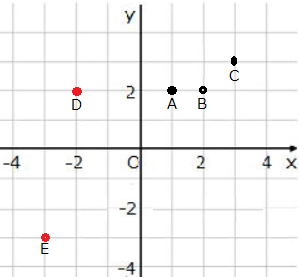 |
1次関数のグラフを時間と容器に増えていく水の量で考えてみよう。
最初から10Lの水が入っている容器に、水を1分間に3Lずつ入れていくとき、
① 容器の水の量と時間はどのような関数で表されるだろうか?
② また、どのようなグラフとなるか?
時間をx、容器の水の量をyとおき、これらの値はどのように変化していくか、
まずは、表で表してみましょう。
| 時間(分) |
0 |
1 |
2 |
3 |
… |
| 容器の水量(L) |
( ) |
( ) |
( ) |
( ) |
… |
③最初、水が入ってなかったら、どのような式になりますか?。
|
 |
|
解説
表は以下のようになりますね。
①1次関数のグラフ
②
| 時間(分) |
0 |
1 |
2 |
3 |
… |
| 容器の水量(L) |
10 |
13 |
16 |
19 |
… |
式として、y=3x+10 (x軸に時間(分) y軸に水の量L)
グラフは傾きが3、切片が10で、おおよそ、右図のように表すことができます。
但し、x≧0
③ 最初、水が入ってなかったら、y=3xになりますよね。
|
 |
■1次関数と方程式
1次関数式は 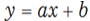 で表す。
で表す。
a:傾き(比例定数) または、変化の割合
b:切片(y軸と交わるところ)
■変化の割合
変化の割合とは、
「xの値が変化した時に、yの値がどれくらい変化したかを調べ、
yの変化量をxの変化量で割った値」のことです。
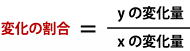 =傾き
=傾き
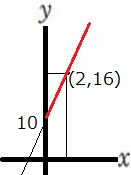
まえに学習した座標の図(右図)を使って、変化の割合を考えてみよう。
例えばA(1,2)とC(3,3)で変化の割合はどのようになっているだろうか?
xは1から3へ。yは2から3に変化している。つまり、
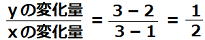 変化の割合(傾き) 変化の割合(傾き)
になります。
y=ax+b のaが変化の割合で傾きになります。
|
 |
問 ① 右上図で、点Dと点Cの変化の割合は?
② 点Eと点Aの変化の割合は?。また、傾きは? |
下は ① =2x ②
=2x ② =2
=2 +1 ③
+1 ③ =2x-2のグラフです。
=2x-2のグラフです。
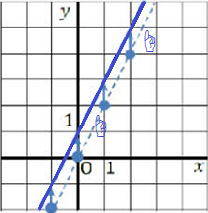
① =2x ②
=2x ② =2x+1 ③
=2x+1 ③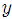 =2x-2
=2x-2
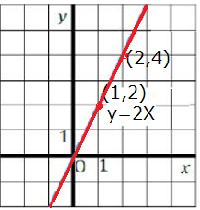
① y=2x は傾きが2、原点Oを通る直線で、中1で学習しましたね。忘れていたら思いだそう!
② y=2x+1は傾きが2、切片が1の直線ですね。
③ y=2x-2は傾きが( )、切片が( )の直線です。( )内に数値を入れてください。
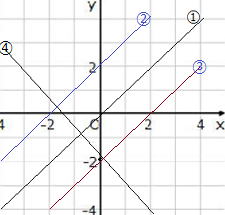
問1 以下の直線を右の表に書き入れなさい。
① y=x ② y=x+2
③ y=x-2 ④ y=- x-2
|
 |
解答
① 中1で学習した原点O(0,0)を通る y=ax の式ですね。
② y=x+2 は傾きa=1、切片2の1次関数グラフです。
③ y=x-2 傾きは①、②と同じ。切片が−2の1次関数グラフ
④ y=-x-2 傾きa=-1、切片−2の1次関数グラフです |
 |
問2 以下の直線を右の表に書き入れなさい。
① 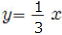 ② ② 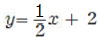
③ 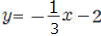 ④ ④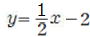
⑤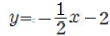 |
 |
問3 次の直線の式を求めなさい。
① x = 1 のとき y = 3 で x = 5のとき y = −1である直線の式。
② 変化の割合が 2で x = 2のとき y= 10である直線の式。
③ グラフの傾きが3で点 (2, 9) を通る直線の式。
④ グラフが点 (1, 2)と点 (2, 8) を通る直線の式。
⑤ x = 3のとき y = 1で、x = 5のとき y = 7である直線の式。
⑥ y =−x+ 9 に平行で x = 1のとき y = 12である直線の式
⑦ 傾きが3で、点(0,2)を通る直線の式。
⑧ 直線 y =3x−2 に平行で、点(4,2)を通る直線の式は
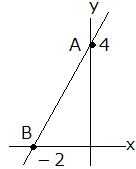
⑨ 右図の直線ℓの式は
⑩ 原点(0,0)と右図の線分ABの中点を通る直線の式は |
 |
|
解説
① x = 1のとき y = 3 で x = 5のとき y = −1である直線の式。
座標(1,3)と(5,−1)で接する直線なので、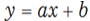 に代入しましょう。
に代入しましょう。
まず、座標(1,3)を代入 3=(a×1) + b 3=a + b…①
次に、座標(5,−1)を代入 −1=(a×5) + b −1=5a + b…②
①-②で 4 = −4a a=−1 b=4
よって y=−x +4 (答)
② 変化の割合が2でx= 2のときy = 10である直線の式。
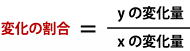 でした。つまり、傾きaのことですね。
でした。つまり、傾きaのことですね。
変化の割合が2だからy=2x + b になります。
座標(2,10)で接する直線なので、10=4+b b=6
よって y=2x + 6 (答) 傾き2、切片6の直線
③ グラフの傾きが3で点 (2, 9) を通る直線の式。
傾きが3だから、y=3 x + b とおきましょう。
y=3 x + b は、点(2,9)を通るので 9=3×2+bより、b=3
よって 求める直線の式は y=3x +3 (答)
④ グラフが点 (1, 2)と点 (2, 8) を通る直線の式。
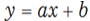 とおく。点(1,2)を通るので
とおく。点(1,2)を通るので
2=a +b …① ※1aの1は省略
8= 2a+b …② ①-②でbを消去しaの値を求めます。
−6=-a より a=6 aの値を①に代入し、b =−4
よって、求める直線の式は y=6 x-4 (答)
⑤ x= 3のとき y =1で、x= 5のとき y =7である直線の式。
⑥ y =−x+9 に平行で x= 1のとき y= 12である直線の式
⑦ 傾きが3で、点(0,2)を通る直線の式。
傾きが3なのでy=3x+bとおく
点(0,2)を通るので、2= b 切片 b=2 よって、求める式は y=3x+2 (答)
⑧ 直線y =3x−2 に平行で、点(4,2)を通る直線は
傾きが3なのでy=3x+b とおく
点(4,2)を通るので、2=12+b b=−10
よって、求める式は y=3x−10 (答)
⑨ 右図の直線ℓの式は
右図から傾き2 切片4であることが分かる
よって、 y= 2x + 4 (答)
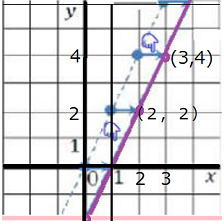
⑩ 原点(0,0)と右図の線分ABの中点を通る直線の式は
ABの中点は(−1,2) y=ax 2=-a
よって y=-2x (答) |
 |
問1 次の中から1次関数をすべて選べ
① y= -5x-2 ② y = 3x2 ③ 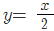
④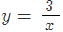 ⑤12x+2y-4=0 ⑤12x+2y-4=0
|
②は二次関数 ④は反比例で1次関数ではない ①,③,⑤が1次関数
例
y= 2x + 8について
① x=-5のときの yの値を求めよ。
② y= 22のときのxの値を求めよ。
|
① y =-2 ② x =7
問2
① y=-5x+3 で、x = 2のときの y の値を求めよ。
② y=6x-11 で、x = 3 のときの y の値を求めよ。
③ y=-x-2 で、x=-8 のときの y の値を求めよ。
⓸ y=7x+15 で、x =6 のときの y の値を求めよ。
⑤ 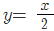 で、x=8のときのyの値を求めよ。 で、x=8のときのyの値を求めよ。
⑥ 2x-3y+1=0 で、x = 4 のときの yの値を求めよ。 |
答
① y=-5x+3 で、x = 2のときのyの値 y=−10+3 y=-7(答) ② y=6x-11 で、x = 3のときの yの値
y= 18-11=7(答)
③ y=-x-2 で、x=-8 のときの yの値を求めよ。 y=8-2 より y=6(答)
問3 次の式を求めよ。
(1) 傾きが2で、切片が4の直線の式
(2) 変化の割合が-3で、x=2,y=-2の一次関数の式
(3) 点(4,1)を通り、切片が9の直線の式 |
解答 (1) y=2x+4
(2) y=−3x+b
−2=(−3)×2+b −2=−6+b ーb=-6+2 −b=-4 b=4
y=−3x+4
まず、y=ax+b とおきましょう。
(2)一次関数の場合、変化の割合は傾きです。
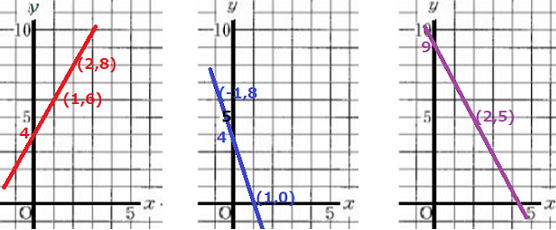
問4 問3で求めた式を下の図に書いてみましょう。
① y=2x+4 ② y=-2x+2 ③ y=-2x+9
   |
解答
① y=2x+4は
切片が4、傾きが2の式
② y=-3x+4は
切片が4、傾きが-3の式
③y=-2x+9は
切片が9、傾きが-2の式 |
 |
■共有点
例題 次の2つの直線の交わった点(座標)を求めなさい。 sum40
① y=x-1 と y=-x+3
|
解説
2直線の式を連立方程式とみて、
連立方程式
y=x-1…①
y=-x+3…② を解くと、
x=2, y=1 交わった点(2,1) |
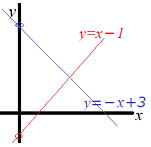 |
問 次の2つの直線の交わった点(座標)を求めなさい。
① y=2x+3 と y=-x-3
② y=−2x+3 と y=-5x+6 |
答
① 2x+3=-x-3 から 3x=−6 x=-2, y = -1 答 (-2, -1)
※ y=2x+3 …① y=-x-3 …② の連立方程式で解いてもOKです。
② −2x+3=-5x+6 から 3x=3 x=1,y=1 答 (1, 1)
■連立方程式の利用
以下の問いは福岡県公立高校入試の問題です。(2020年)
問1 ある携帯電話会社には携帯電話の1カ月の料金プランとしてAプラン、Bプラン、Cプランの3種類がある。
どのプランも電話料金は基本使用料と通話時間に応じた通話料を合計した料金である。
右の表は3つのプランを示したものです。 |
| |
電話料金 |
| 基本使用料 |
通話時間に応じた通話料 |
| Aプラン |
1,200円 |
60分までの時間は、1分あたり40円
60分をこえた時間は、1分あたり30円 |
| Bプラン |
(ア)円 |
(イ)分までの時間は無料
(イ)分をこえた時間は1分あたり(ウ)円
|
| Cプラン |
3,900円 |
60分までの時間は無料
60分をこえた時間は、1分あたり一定の料金がかかる |
|
【右図1】はAプランをグラフに表したものです。1カ月に 分通話したときの電話料金を 分通話したときの電話料金を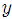 円とし、通話時間が0分から90分までの 円とし、通話時間が0分から90分までの と と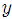 の関係を示しています。 の関係を示しています。
次の(1)~(3)に答えよ。
(1) Aプランについて、電話料金が3,000円のときの通話時間を求めなさい。 |
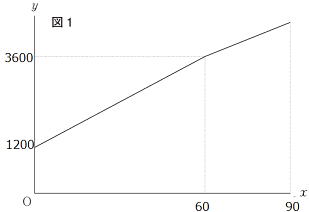 |
解説 (1) Aプランの基本料金は1,200円、それに通話料を加算した価格が3,000円なので、
(グラフより基本料金を加えた料金は60分までで3,600円) 60分内ということが分かります。
通話時間を 分とおくと、基本使用料+40
分とおくと、基本使用料+40 =3000 1200+40
=3000 1200+40 =3000
=3000  =45 45分 (
=45 45分 ( <60)
<60)
(2)
【右図2】はBプランをグラフについて通話時間が0分から90分までの と と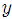 の関係を表したグラフを、図1に書きいれたものです。 の関係を表したグラフを、図1に書きいれたものです。
以下はBプランについて と と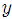 の関係を表した式です。 の関係を表した式です。
Bプランについて と と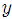 の関係を表した式 の関係を表した式
 の変域が0≦ の変域が0≦ ≦20のとき、 ≦20のとき、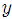 =2300であり、 =2300であり、
 の変域が20≦ の変域が20≦ ≦90のとき、 ≦90のとき、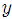 =a =a +b(a,bは定数)である。 +b(a,bは定数)である。
ただし、 =60のとき、 =60のとき、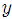 =3300である。 =3300である。
【右図2】をもとに、以下の表の(ア),(イ),(ウ)にあてはまる数を、それぞれ答えよ。
| Bプラン |
(ア)円 |
(イ)分までの時間は無料
(イ)分をこえた時間は1分あたり(ウ)円 |
|
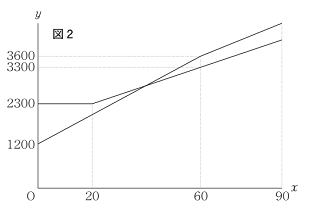 |
解説(2) (ア) Bプランの基本料金は右のグラフより2,300円であることが分かります。 2,300円 …答
(イ) 右のグラフより20分であることが分かります。 20分 …答
(ウ) グラフより20分以上の傾きを座標から考えます。(60−20)、つまり40分で(3300-2300)=1000なので、
1分あたり1000/40=25 25円… 答
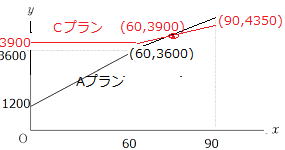
(3) Cプランの電話料金は通話時間が90分のとき4,350円である。
通話時間が60分から90分までの間で、Cプランの電話料金がAプランの電話料金より安くなるのは、通話時間が何分をこえたときからか求めよ。 解答は右の条件Ⅰ~Ⅲにしたがってかけ。 |
【条件Ⅰ】 AプランとCプランのそれぞれについて、グラフの傾きやグラフが通る座標を示し、 と と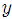 の関係を表す式を書くこと の関係を表す式を書くこと
【条件Ⅱ】 条件Ⅰで求めた2つの式を使って答を求める過程をかくこと |
| Cプラン |
3,900円 |
60分までの時間は無料
60分をこえた時間は、1分あたり一定の料金がかかる |
|
解説(3) 実際にグラフ上に書き込んでみましょう。Cプランで60分以上90分以下の通話時間を (分)とおく。60≦ (分)とおく。60≦ ≦90 ≦90
Aプランはグラフより(60,3600), 傾きが30なので
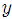 =30 =30 +bより 3600=30×60+b b=1800 +bより 3600=30×60+b b=1800
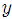 =30 =30 +1800…① +1800…①
Cプランはグラフ上の座標(60,3900), (90,4350)を通るので
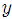 =15 =15 +3000…② +3000…②
①,②より  =80 通話時間が80分をこえたときから …答 =80 通話時間が80分をこえたときから …答 |
 |
問2
 |
■平行と合同 
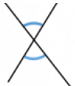
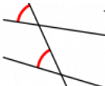
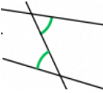
復習問題 下の図の角度のことをそれぞれ何角といいますか?
① ② ③ |
①対頂角 ②同位角 ③錯覚
一般的に②,③は平行な線で出題されることが多いです。
① x=50°②180-(42+31)=107° ③x=69° y=67°)
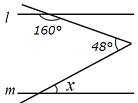
問2 ℓ ∥ m のとき、∠x、∠y の大きさをそれぞれ求めなさい。
①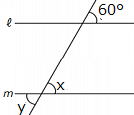 ② ②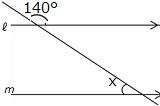 ③ ③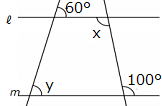
|
① x=60°y=60° ②40° ③ x=100°,y=60°
問3 ℓ // m のとき、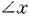 ,∠ y の大きさをそれぞれ求めなさい。 ,∠ y の大きさをそれぞれ求めなさい。
①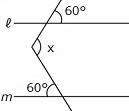 ② ②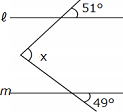 ③ ③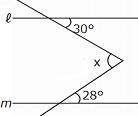 |
答 ① 28° ②52°
こうした問題は線を補うことにより、簡単に解決することがあります。
■多角形の角
▲三角形の内角と外角
|
ΔABCに、辺BCの延長CDを引きます。
CからAB∥CEの直線CEを引きます。以下の問いをやってみよう
①∠a+∠b=(∠ )で三角形の1つの外角は、それと隣り合わない2つの内角の和に等しいから。
②∠b=と等しい角は( )で (同位角/対頂角/錯覚)であるから。
③∠a=と等しい角は( )で (同位角/対頂角/錯覚)であるから。
|
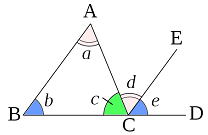 |
答 ① ∠ACD (または∠d+∠e) ∠DCAでも可
② ∠e で同位角
③ ∠d で錯覚
▲多角形の角
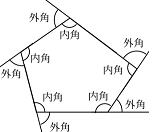
n角形の内角の和= 180°×(n−2) しっかり覚えておこう‼
問 次の角の大きさを求めなさい。
(1) 五角形の内角の和を求めなさい。
(2) 正八角形の1つの内角の大きさを求めなさい。
|
答
(1) 180×(5−2)= 540°
(2)正八角形の内角の和は=1080°なので、1つの内角の大きさは135°
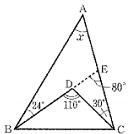
| 問1 次の①~④の ∠x の大きさを求めなさい。 |
① 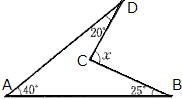 |
②正六角形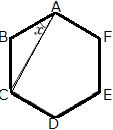 |
③ AB=AC,∠ACD=∠BCD
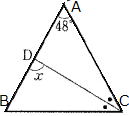 |
④ 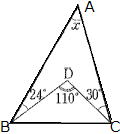 |
答 ①85°②30°③33°④56°(下図参考)
■合同
・ 合同とは、「2つ以上の図形がピッタリと重ね合わせられるときの関係」をいいます。
・ 合同を数式で表すときは、「≡」を用います。
・ 合同な図形は対応する「角」「辺の長さ」が等しくなる。
▲三角形の合同証明
以下の3つの合同条件は必ず覚えること
三角形の合同条件
① 3組の辺がそれぞれ等しい。
② 2組の辺とその間の角がそれぞれ等しい。
③ 1組の辺とその両端の角がそれぞれ等しい。 |
① 3組の辺がそれぞれ等しい。

② 2組の辺とその間の角がそれぞれ等しい。

③ 1組の辺とその両端の角がそれぞれ等しい。

| 右の三角形と合同な三角形を下のアからエまでの4つの中から1つ選び、合同条件を書きなさい。 |
 |
 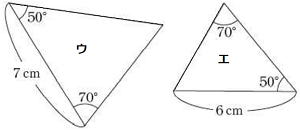 |
答 ア まず、求められる角度は図に書き込もう。
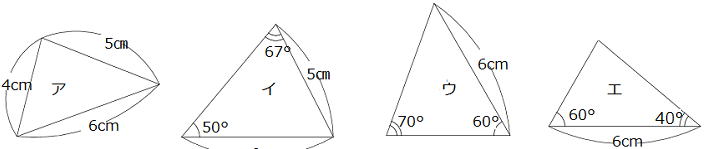
| 問 下の図アからクまでの三角形で合同な三角形の組を選びなさい。また、そのとき使った合同条件を書きなさい。

|
解答 まず、求められる角度は図に書き込もう。
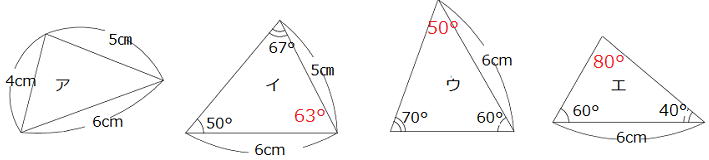

アとカ 合同条件:3辺がそれぞれ等しい
イとオ 合同条件:2辺とその間の角がそれぞれ等しい
エとク 合同条件:1辺とその両端の角がそれぞれ等しい。
問 下の直角三角形△ABC,△GHIと合同な直角三角形は。
またその時に使った直角三角形の合同条件を答えなさい
△ABC≡ △( ) 合同条件( )
△GHI ≡ △( ) 合同条件( )
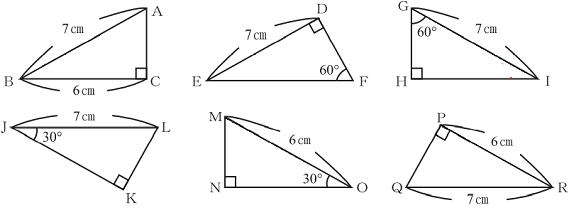 |
△ABC≡ △(QRP) 合同条件(斜辺と他の一辺がそれぞれ等しい)
△GHI ≡ △(LKJ) 合同条件(斜辺と1つの鋭角がそれぞれ等しい) )
例題1
AB=CB、AD=CDのとき∠BAD=∠BCDであることを証明しなさい。 |
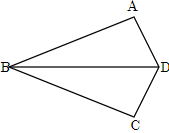 |
知りえた情報(データ)は図に書き込みましょう。
△ABD≡△CBD(△BAD≡△BCDでもOK)であることを証明したのち、
∠BAD=∠BCDであることを証明します。
【証明】 △ABDと△CBDにおいて
仮定より AB=CB…①, AD=CD…②
BD=BD(共通)…③
3組の辺がそれぞれ等しいので
△ABD≡△CBD
合同な図形の対応する角は等しいので
∠BAD=∠BCD |
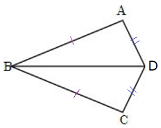 |
問1 右図でAB=DC,AC=DBならば、
△BAC≡△CDBであることを証明しなさい。 |
 |
知りえた情報(データ)は図に書き込みましょう。
証明 △BACと△CDBにおいて
仮定より AB=DC
仮定より AC=DB
BC=CB (共通) よって3組の辺がそれぞれ等しいので
△BAC≡△CDB |
 |
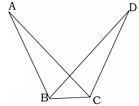
問2 右図でAD=AE,∠ADC=∠AEBのとき、
△ACD≡△ABEであることを証明しなさい。 |
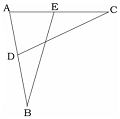 |
[証明] △ACDと△ABEにおいて
AD=AE (仮定)
∠ADC=∠AEB(仮定)
∠DAC=∠EAB(共通)
よって1組の辺とその両端の角がそれぞれ等しいので
△ACD≡△ABE |
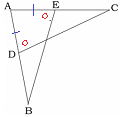 |
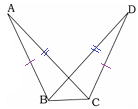
[証明]
△ADEと△DBFにおいて、仮定より AD=DB……①
DE∥BCより,∠ADE=∠( DBF )……②
DE∥BCより,∠DAE=∠( BDF )……③
①,②,③,より(1組の辺とその両端の角 )がそれぞれ等しいので
△ADE≡△DBF よって、( DE=BF )
p58 サミングアップ
例題2 右図のようにAD∥BCである台形ABCDの対角線ACの中点Oを通る直線が、辺AD,BCと交わる点をそれぞれE,Fとする。AE=CFを次のように証明した。□をうめなさい。
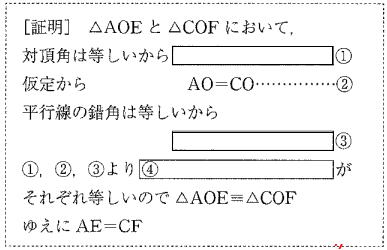 |
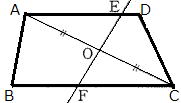 |
答
①∠AOE=∠COF ②∠OAE=∠OCF ③1組の辺とその両端の角
注) ∠OEA=∠OFCも確かに等しいのだが、「1組の辺とその両端の角」を満足させないので
合同の証明の対象にはなりません。
| 問3 右図のようにAD∥BCである台形ABCDの対角線ACの中点Oを通る直線が、辺AD,BCと交わる点をそれぞれE,Fとする。AE=CFを証明しなさい。 |
 |
上の例題と同じ問題です。
▲直角三角形の合同
・斜辺と他の1辺がそれぞれ等しい
・斜辺と他の1つの鋭角がそれぞれ等しい
問1 図の直角三角形でABCで斜辺AC上にBC=DCとなる点Dをとり、Dを通りACに垂直な直線とABとの交点をEとする。△BCE≡△DCEを証明せよ。
|
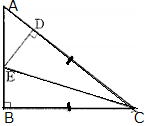 |
証明 △BCEと△DCEで
仮定より∠EBC=∠EDC=90° …①
BC=DC …②
ECは共通 …③
①,②,③より直角三角形の斜辺と他の1辺がそれぞれ等しいので△BCE≡△DCE
| 問2 図のように、正方形ABCDの頂点Bを通り辺ADと交わる直線mに、A,Cからから垂線をひき、mとの交点をそれぞれE,Fとする。AE=BFを証明せよ。 |
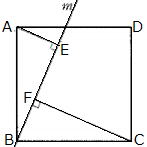 |
証明 △ABEと△BCFで
仮定より ∠AEB=∠BFC=90° …①
AB=BC …②
次に∠ABEと∠BCFについて
∠ABE+∠FBC=90°…③
∠BCF+∠FBC=90°…④
③,④より∠ABEと∠BCF…⑤ がいえる。
①,②,⑤より直角三角形の斜辺と1つの鋭角がそれぞれ等しいので
△ABE≡△BCF よって、AE=BF
問3 右図で点D,EはそれぞれAB,AC上の点で、BEとCDの交点をPとし、AB=AC,AB⊥CD,AC⊥BEである。
このとき、以下の証明をしなさい。
(1) AD=AE
(2) △BDP≡△CEP |
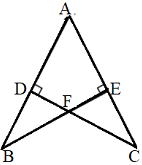 |
解答 必ず、分かった情報は図に書き込みましょう。
(1) AD=AE の証明
△ABEと△ACD において、
仮定より、
AB=AC ・・・①
∠AEB=∠ADC=90° ・・・②
共通な角なので、
∠BAE=∠CAD ・・・③
(1),(2),(3)より、斜辺と1つの鋭角がそれぞれ等しいので、
△ABE≡△ACD
合同な図形の対応する辺は等しいので、 AD=AE
(2) △BDF≡△CEF
△BDFと△CEF において、
仮定より、AB=AC
(1)より、AD=AEなので、
DB=AB-AD EC=AC-AE
DB=EC ・・①
仮定より、 ∠BDF=∠CEF= 90° ・・・②
(1)より、 ∠DBF=∠ECF ・・・③
①,②,③より、1組の辺とその両端の角がそれぞれ等しいので、
△BDF≡△CEF |
 |
・長方形とひし形の特徴
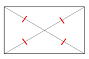
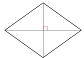
長方形:対角線の長さが等しい ひし形:対角線が垂直に交わる


■確率
確率は以下の順番で解決していこう。
①樹形図をかく ②すべての場合の数を調べる
③あることがらの場合の数を調べる
④確率を公式で計算 
約分するのを忘れないで。確率の値は1以上になることはありません
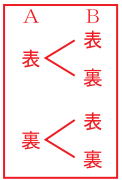
| 例題 ABC3枚のカードを並べるとき、BとCが隣り合わせになる確率について考えてみよう。 |
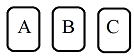 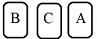 や や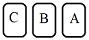 など など |
解説)
まず、①樹形図をかいてみよう(左図)
②すべての場合の数は左図から6通り ですね
③あることがらの場合の数を調べる。ここではBとCが隣り合わせだから(赤で囲った) 4通り
④確率を公式で計算 4/6=2/3 (3分の2) |
図1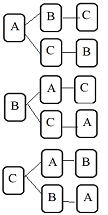 図2 図2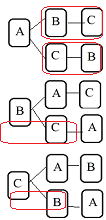 |
練1 1個のさいころを投げるとき、次の確率を求めよ。
① 奇数の目がでる確率 ② 5以上の目がでる確率 ③2以下の目がでる確率
練2 赤玉3個、白玉2個が入っている袋から1個取り出すとき、白玉が出る確率は?
練3 1枚の100円硬貨を2回投げるとき、2回とも同じ面がでる確率を求めよ。
練4 52枚のトランプから1枚のカードを引くとき、引いたカードがハートである確率は?
(トランプにはスペード♠、ハート💛、クローバー♧、ダイヤ♦の4種類があります)
練5 ジョーカーを除く52枚のトランプから1枚のカードを引くとき、次の確率を求めなさい。
① 7のカードを引く確率
② 絵札を引く確率
それぞれの絵札カードにJoker Queen Kingの3種類があります。
|
答) 練1) ①1/2 ②1/3 5と6の2通り ③1/3 練2) 2/5 練3)1/2
練4)答 1/4
練5)答 ジョーカーを除く52枚のトランプから1枚のカードを引くとき、
① 7のカードを引く確率 4/52=1/13
② 絵札を引く確率 12/52=3/13
13×4種類=52枚 絵札12枚 |
 |
問1 10円硬貨1枚と100円硬貨1枚を同時に投げるとき、両方とも表面がでる確率を求めなさい。
問2 大小2個のさいころを同時に投げるとき、目の和が8になる確率は
問3 大人3人と子供4人の中から2人を選ぶとき、2人とも子供である確率は? |
問1答 起こりえるすべての結果は4通りであり、これらは同様に確からしい。
そのうち2枚とも表が出るのは1通りであるから、求める確率は1/4
以下の表以外に、樹形図を用いてもいいですね。 |
|
問2答 5/36 図1,2どちらでも良いですね。
図1 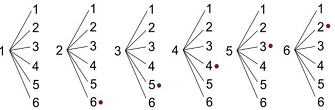
大きい方のサイコロを中心に書いています |
図2 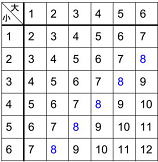 |
問3 2/7
確率などに強くなるには数多くの問題に接し、慣れることです。
問4 1から5までの数を書いた5枚のカードがある。
①この中から1枚カードを引くときに奇数が出る確率を求めなさい
②2枚連続で引くときに両方とも奇数になる確率を求めなさい。
ただし、1回目に引いたカードはもとにもどさない。
|
解説
① 全ての場合の数は5枚。1〜5のうち奇数は1,3,5の3枚だから、確率は3/5。
② 全ての場合の数は5枚引き、続けて4枚引くので5×4=20通り。
そして、連続して奇数となるのは、(1,3), (1,5),(3,1),(3,5),(5,1),(5,3)の6通りです。
(難しかったら、樹形図を書いてみましょう)
つまり20通りのうち、奇数が6通りなので、確率は6/20。約分をして、答えは3 /10。
問5 2枚のコインを同時に投げるとき、次の確率を求めなさい。
① 2枚とも表が出る確率
② 表と裏が1枚ずつでる確率 |
解説 − 右の図を参考 −
起こりえるすべての場合の数は4通り。
①2枚とも表の場合は1通り
よって1/4
②表と裏が1枚ずつ出る場合は2通り。
よって1/2 |
 |
問6 1,2,3,4の数字が1つずつ書かれた4枚のカードがある。
このカードを続けて2枚引き、はじめに引いたカードを十の位、
次に引いたカードを一の位として2桁の整数をつくる。
次の確率を求めなさい。ただし引いたカードは元に戻さないものとする。
(1) できた整数が奇数になる確率
(2) できた整数が4の倍数になる確率 |
解説
(1)はすぐに分かるが、この場合、樹形図を書いてみよう。
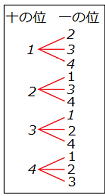 (1)すべての場合の数は12通り。
(1)すべての場合の数は12通り。
答 (1)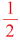 (2)
(2) 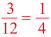
問7 赤玉2個、青玉3個が入れた袋から、同時に2個取り出すとき、次の確率を求めなさい。
(1) 赤玉が1個、青玉1個出る確率
(2) 青玉が2個出る確率
(3) 赤玉が少なくとも1個出る確率 |
解説
樹形図を書いてみよう。下の図から、全ての場合の数は10になるね。
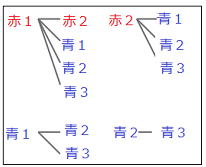
(1) 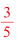 (2)
(2)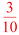 (3)
(3)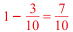
 中1の復習問題
中1の復習問題
 数学は皆さんを苦しめるためにあるのではありません。
数学は皆さんを苦しめるためにあるのではありません。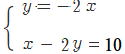 ②
②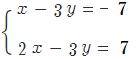 ③
③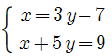
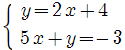 ⑤
⑤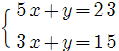
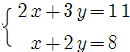 ⑧
⑧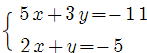
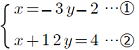
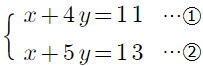 (2)
(2)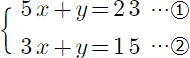 (3)
(3)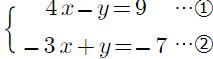
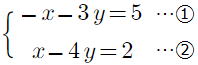 (5)
(5)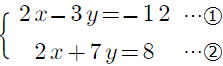 (6)
(6)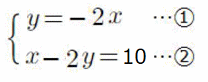
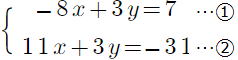 (8)
(8) 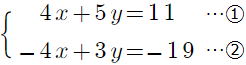
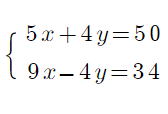 (10)
(10)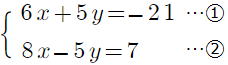




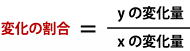 =傾き
=傾き














 ②
② ③
③ 
 ②
② ③
③
 ②
② ③
③
 ②
② 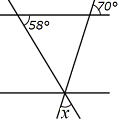
































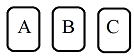
 図2
図2




 (1)すべての場合の数は12通り。
(1)すべての場合の数は12通り。