① 3−(−4)= ② 7×(−4)−(−2)= ③ 4−2×(−3)=
④ 15÷(−3)+2= ⑤ −22+(−3)2=
⑥
中2サミングアップ 戻る
■ 文字式 p6
| 問1 次の計算をしなさい。 ① 3−(−4)= ② 7×(−4)−(−2)= ③ 4−2×(−3)= ④ 15÷(−3)+2= ⑤ −22+(−3)2= ⑥ |
答
⑤ −22+(−3)2=−4+9=5 ⑦![]() =6
=6
p9 ◆類題4
| 問2 ① ② ③ |
答
①![]() =−9 ②
=−9 ②![]() ③
③![]()
■式の利用 p14
| 問3 (1) 連続する3つの整数の和は、中央の数の3倍に等しいことを証明せよ。 (2) ある2けたの自然数と、その数の一の位と十の位の数字を入れかえた自然数の和は11の倍数になることを示せ。 |
解説
(1) 中央の数をnとおくと、3つの連続する整数はn−1,n, n+1と表すことができる。
(最小の値をn おいても可)
よって3つの整数の和は(n−1)+n+(n+1)=3n となりn は整数だから中央の数の3倍に等しい。
(2) ある2けたの自然数を10![]() +
+![]() とおくと、一の位と十の位の数字を入れかえた自然数は10
とおくと、一の位と十の位の数字を入れかえた自然数は10![]() +
+![]() と表せる。
と表せる。
和は(10![]() +
+![]() )+(10
)+(10![]() +
+![]() )で 11
)で 11![]() +11
+11![]() となり、11(
となり、11(![]() +
+![]() ) よって11の倍数になる。
) よって11の倍数になる。
等式・不等式・方程式 p18
| 問4 次の数量の関係を式で表せ。 (1) 2数 (2) 500mの道のりを毎分80mで (3)1個 |
解説
(1) 4(![]() +
+![]() )>
)>![]() (2) 500−80
(2) 500−80![]() =70 (3) 0.7
=70 (3) 0.7![]() ×5≧10000
×5≧10000
p18
| 問5 次のア~オの方程式のうち、 ア エ 2 |
p22
| 問6 ① |
p22
|
問7 次の連立方程式を解きなさい。
|
比例・反比例p34
| 問8 次の文の (1) (2) 底辺 (3)おもり1㎏につき0.5㎝伸びるバネに、 |
p37 類題3
| 問9 次の直線の式を求めよ。 (1)直線 (2)2点、(4,8)、(−3,−13)を通る直線 (3)点(−2,5)を通り、 |
p38
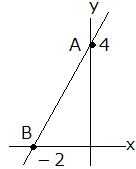
| 問10 (1) 傾きが3で、点(0,2)を通る直線の式。 (2) 直線y =3x−2 に平行で、点(4,2)を通る直線は (3) 右図の直線ℓの式は (4) 原点(0,0)と右図の線分ABの中点を通る直線の式は |
 |
解説
| (1) 傾きが3なのでy=3x+bとおく 点(0,2)を通るので、2=b 切片b=2 よって、求める式はy=3x+2 (答) (2) 直線y =3x−2 に平行で、点(4,2)を通る直線は 傾きが3なのでy=3x+bとおく 点(4,2)を通るので、2=12+b b=−10 よって、求める式はy=3x−10(答) (3) 右図の直線ℓの式は 右図から傾き2 切片4であることが分かる よって、 y=2x+4 (答) (4) 原点(0,0)と右図の線分ABの中点を通る直線の式は ABの中点は(−1,2) y=ax 2=-a よって y=−2x (答) |
 |
p40
-----------------------------------------------------------------------------------
p58
| 問 次の①~④の |
|
① 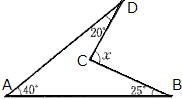 |
②正六角形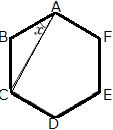 |
③ AB=AC,∠ACD=∠BCD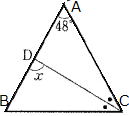 |
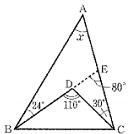
④ 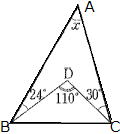 |
答 ①85°②30°③33°④56°(下図参考)
n角形の内角の和= 180°×(n−2)
| 問 次の角の大きさを求めなさい。 (1) 五角形の内角の和を求めなさい。 (2) 正八角形の1つの内角の大きさを求めなさい。 |
答
(2)正八角形の内角の和は=1080°なので、1つの内角の大きさは135°
■合同
▲三角形の合同
以下の3つの合同条件は必ず覚えること
① 3組の辺がそれぞれ等しい。

② 2組の辺とその間の角がそれぞれ等しい。

③ 1組の辺とその両端の角がそれぞれ等しい。

| 例題 AB=CB、AD=CDのとき∠BAD=∠BCDであることを証明しなさい。 |
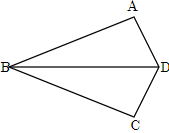 |
【証明】
△ABDと△CBDにおいて
仮定より AB=CB, AD=CD
共通なので BD=BD
よって3組の辺がそれぞれ等しいので
△ABD≡△CBD
合同な図形の対応する角は等しいので
∠BAD=∠BCD
p58 サミングアップ
例題 右図のようにAD∥BCである台形ABCDの対角線ACの中点Oを通る直線が、辺AD,BCと交わる点をそれぞれE,Fとする。AE=CFを次のように証明した。□をうめなさい。 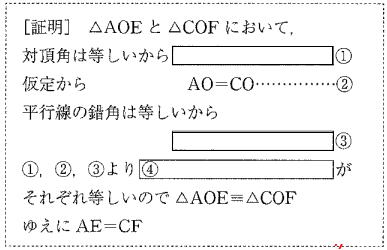 |
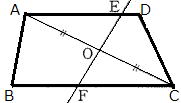 |
答
①∠AOE=∠COF ②∠OAE=∠OCF ③1組の辺とその両端の角
| 問1 右図のようにAD∥BCである台形ABCDの対角線ACの中点Oを通る直線が、辺AD,BCと交わる点をそれぞれE,Fとする。AE=CFを証明しなさい。 |  |
上の例題と同じ問題です。
▲直角三角形の合同
・斜辺と他の1辺がそれぞれ等しい
・斜辺と他の1つの鋭角がそれぞれ等しい
| 問1 図の直角三角形でABCで斜辺AC上にBC=DCとなる点Dをとり、Dを通りACに垂直な直線とABとの交点をEとする。 △BCE≡△DCEを証明せよ。 |
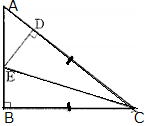 |
証明 △BCEと△DCEで
仮定より∠EBC=∠EDC=90° …①
BC=DC …②
ECは共通 …③
①,②,③より直角三角形の斜辺と他の1辺がそれぞれ等しいので△BCE≡△DCE
| 問2 図のように、正方形ABCDの頂点Bを通り辺ADと交わる直線mに、A,Cからから垂線をひき、mとの交点をそれぞれE,Fとする。 AE=BFを証明せよ。 |
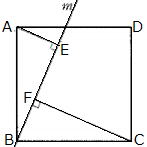 |
証明 △ABEと△BCFで
仮定より ∠AEB=∠BFC=90° …①
AB=BC …②
次に∠ABEと∠BCFについて
∠ABE+∠FBC=90°…③
∠BCF+∠FBC=90°…④
③,④より∠ABEと∠BCF…⑤ がいえる。
①,②,⑤より直角三角形の斜辺と1つの鋭角がそれぞれ等しいので△ABE≡△BCF
よって、AE=BF
資料の整理
| 右の表は40人の生徒の体重をはかり、度数分布表に整理したものである。次の問いに答えなさい (1) ①45㎏~50㎏ ②60㎏~65㎏の階級について、相対度数を求めなさい。 (2) 度数分布表を完成させなさい。 (3) 度数分布表をもとに、生徒の体重の平均値を求めなさい。 |
|
答 (1) ①0.4 16/40=2/5=0.4 ②0.05 2/40=0.05 (2)下図 (3)50㎏
| 体重㎏ | 階級値(㎏) | 度数(人) | 階級値×度数 |
| 以上 未満 40~45 |
42.5 | 6 | 42.5×6=255 |
| 45~50 | 47.5 | 16 | 47.5×16=760 |
| 50~55 | 52.5 | 12 | 52.5×12=630 |
| 55㎏~60 | 57.5 | 4 | 57.5×4=230 |
| 60~65 | 62.5 | 2 | 62.5×2=125 |
| 計 | 40 | 2000 |
相対度数
| 問 右の表は、あるクラスで1日のテレビの視聴時間を調べた記録である。 空欄( |
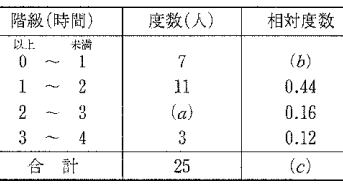 |
答 (![]() ) 25-(7+11+3)=4 (
) 25-(7+11+3)=4 (![]() ) 7÷25=0.28 相対度数は各階級の度数を相対度数の合計で割った値です。
) 7÷25=0.28 相対度数は各階級の度数を相対度数の合計で割った値です。
(![]() )1.00 相対度数の合計は1.00(100%)
)1.00 相対度数の合計は1.00(100%)
p66
| 問 右のヒストグラムはあるクラスの身長の記録である。 ①身長の高い方から数えて10番目の生徒はどの階級に入るか。 ②140㎝以上170㎝未満の生徒の割合は何%か。 |
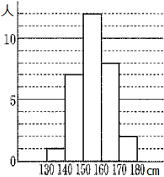 |
答
① 160㎝以上170㎝未満 8+2=10(人)
② 90% 140㎝以上170㎝未満の生徒数は7+12+8=27
クラス全体の数 1+7+12+8+2=30人なので (27/30)×100 = 90%
代表値・平均
p66
| 問 右の表はAさんが25日間のバスの待ち時間を調べた結果である。 次の問いに答えよ。 ① 右表の□を埋めよ。 ② 最頻値を答えよ。 ③ 待ち時間の平均を求めよ。 |
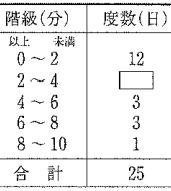 |
答 ① 6 ② 1分 ③ 3分
階級値はそれぞれ1、3、5、7、9 度数はそれぞれ12、6、3、3、1 度数の合計は25日
(1×12)+(3×6)+(5×3)+(7×3)+(9×1)=12+18+15+21+9=75 75÷25=3
p67
| 問 右のヒストグラムで、①,②,③はそれぞれ中央値、最頻値、平均値のどれか、答えなさい。 ① ② ③ |
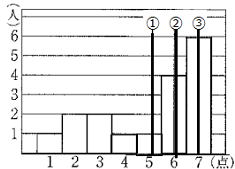 |
①平均値 ②中央値 ③最頻値

1 4 6 4 5 24 42 合計86点 17人 平均値 86÷17=5.05
中央値は順位が中央の値 最頻値は度数が一番多い値
-------------------------------------------
福岡県入試問題

1年生は100人なので真ん中は50人−− 上から数えて10~15が入ります。
いっぽう、3年生は105人。奇数なので105÷2=52.5で階級5~10に中央値が含まれます。
1年生のほうが中央値は大きい。中央値が含まれる階級は1年生の階級10~15…答
■近似値 有効数字
サミングアップ p66
| 問 ある数aの十の位を四捨五入すると 2700になった 誤差の絶対値は最大でいくつですか |
解答
2700は、2650から、2749 (2700-2650)=50で 50。
| 問 ある数bの小数第2位を四捨五入すると5.0になった。bの範囲を不等号を用いて表せ。 |
答 4.95≦ b <5.05
4.94では小数第2位を四捨五入すると4.9になります。4.95なら5.0 よってbは4.95以上
反対に5.05では小数第2位を四捨五入すると5.1になります。
| 問 地球の直径12800kmをmを単位としてあらわすと1.28×10nである。nの値は |
解答
まず12800kmは1.28×10000㎞ → 1.28×104km
1.28×104km をmに直すと、(1.28×104)×103 よって1.28×107 n=7