数A
　　目次　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　☜　　戻る

6月10日は時間がありませんでしたので、以下に説明します。

　１から13まで偶数のカードは６枚、奇数のカードは7枚あります。
　偶数のカードは６枚の中から２枚、奇数のカードから１枚を選ぶ
(単に選ぶだけで順番に並べるのではないので)
　₆C₂＝15　偶数のカードそれぞれに対し、奇数のカードを選ぶ選び方は
　₇C₁＝７で,積の法則により、₆C₂×₇C₁＝105　となります。(2023/6/11)

　2　集合の要素の個数　　ｎ:number

${}_{\mathrm{答） 集合の要素の個数を問う問題です。}}$${}_{\mathrm{(1) ｎ(A)=20 (2)\; n(B)=15 (3) ｎ(A\cap B)=5\; \; (4) n(A\cup B)=30 \; \; (5)\; =15}}$${}_{\mathrm{(1)\; 集合A=｛３,６,９,12,15,18,\; 21,24,27,30.33.36.39,42,45,48,51,54,57,60｝n(A)=20\; (2)\; 集合B=｛4,8,12,16,20,24,28,32,36,40,44,48,52,56,60｝n(B)=15}}$　(1)、(2)は単に60÷3=20　　60÷4=15 で計算してもOK。ｎ(?)=n(U)-n(a)=60ー20=40

　(4) (A∩B)={12,24,36,48,60}よりｎ(Ａ∩Ｂ）=5

　(5) ｎ(A∪B)= n(A)+n(B)－ｎ(Ａ∩Ｂ）より20+15－５=3０

　数学は如何にして問題解決する学問だと思いますが、
　以下に実際に上のような問題を楽してやってみましょう。

　　答
　　(1) ４の倍数は何個あるか。4,8.12.16…　　
　　　　　　　　　　　　　　　　２００÷４=５０　n(A)=50
　　(2) ５の倍数は何個あるか。　　２００÷５=４０　n(B)=40
　　(3) ４の倍数、かつ５の倍数は何個あるか　 A∩ B→20の倍数
　　　　　n (A∩ B)= 10　　または200÷20
　　(4) ４の倍数または、５の倍数は何個あるか。A∪Ｂ
　　　　　n(A ∪ Ｂ) = n(A)+n(B)ーn(A∩ B) =50+40-10= 80
　　(5) ４で割り切れない数は何個あるか。
　　　　　　割り切れる数を求めよう。
　　　　　n()= 200－n(A)= 200-50=150
　　(6) ５で割り切れない数は何個あるか。
　　　　　n()= 200－n() =200-40=160
　　(7) ４でも５でも割り切れない数は何個あるか。
　　　　　　割り切れる数を求めよう。
　　　　　 = 200 ー n(A∪B) =200-80 =120
　　(8) ４で割り切れるが、５では割り切れない数は何個あるか。
　　　　　　４で割り切れる数はn(A)個。
　　　　　n(A) ー n(A∩B ) = 50 - 10=40　
　　しっかり基礎を学び、前向きに考えることで、次第に楽して解けていくようになるでしょう。
　　3　和の法則と積の法則

　　　和の法則

右図のように道路がある町で、交差点Oから交差点Hまで遠回りしないで行く最短の道順は何通りあるでしょう。 樹形図を用いてもOKです。

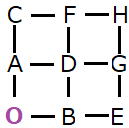　　まずOA、OB。OAに対しAC,ADと　　　　　答　6通り

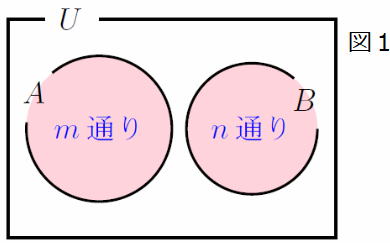
図１をみてみましょう。 　２つの事柄AとBがあり、Aがｍ通り、Bがｎ通りのとき、AとBが同時に起きないとすると、 　　　　以下の通りAまたはBの一方が起きる場合の数はｍ+ｎ通り。　集合でとらえると当たり前ですね。 　　　　共通部分がない（A∩B＝） ｎ（A∪B）=ｎ（A）+ｎ（B）　和集合の要素の個数 　　集合AとBは互いに排反であるといいます。

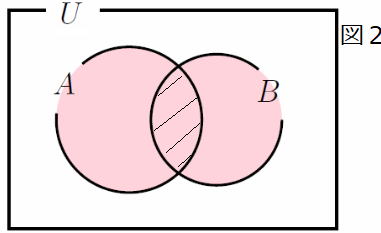
　　しかし、下の図２のようにAとBが排反でない場合はどうだろう。
　　　　

図１と図２の違いは、重要なポイントを示唆しています。 　つまり、Aの場合の数とBの場合の数を足す場合、同時に起こるか否かを確認することが重要になります。 　同時に起こらない場合のみ和の法則が成り立ち、 　　　図２のように、同時に起こる場合はダブルカウントになり、 　　　　　n(A∪B)=ｎ(A)+n(B)−ｎ(A∩B）と、 　　　　　　和の法則は成立しません。

解説
　　目の和が１０になる場合　４と６　５と５　６と４　　の３通り
　　目の和が１１になる場合　５と６　６と５　の３通り　　これら２つの場合は同時に起こることはないため
　　目の和が１０　または１１になる場合の数は　３＋２＝５通り　となります。

　答
　　　(1) 目の和が４の倍数は大小２つのさいころなので、４と８と１２　　９通り…答
　　　(2) 目の和が３の倍数は大小２つのさいころなので、３と６と９と１２　　１２通り…答

　　　　分からなかったら図を描いてみよう。もちろん和の法則だよね。

------------------------------------------------------------------2020/10/06----宿

　　１０通り … 答

　　積の法則

　　答　Ａ地点からＢ地点まで３通りあり、そのそれぞれについて
　　　　Ｂ地点からＣ地点までの生きかたが４通りあるので、
　　　　３×４=１２通り　になります。

1,2,4,8 / 1,3,9 /　　1-1, 1-3, 1-9　 2-1, 2-3, 2-9　4-1, 4-3, 4-9　　8-1, 8-3, 8-9
　　　　　　　　　 １　３　９　 ２　６　18　　4　12　36　　 8　24　72
　　　　　　　　　　　　　　　　 　1, 2, 3, 4, 6, 8, 9. 12, 18, 24, 36, 72　の12個

答
　　① １２５＝５×５×５ = ５^３　　1、５、２５、１２５　　４個

　　② ４０＝２^３×５^１　　４×２＝８個　1,2,4,5,8,10,20,40

　　③ １０８＝２^２×３^３　　３×４＝１２個

解答
　　A：2回表が出る場合とB：３回表が出る場合が考えられる。
　　　Aが起きる場合の数は「表表裏」「表裏表」「裏表表」の３通り，

　　Bが起きる場合の数は「表表表」である。
　　　よって，和の法則よりAまたはBが起きる場合の数は３＋１＝４通りである。

　４．順列と組合せ

　　教科書では順列から始めますので、組み合わせと順列の違いで戸惑う生徒さんが多いようです。

　それでは、順列と組み合わせの違いから説明しましょう。

　　順列…　異なる $n$個のものから $r$ 個を選んで、一列に並べる　…　${}_n{P}_{\mathrm{r 公式}}$

　　組合せ…異なる $n$個のものから $r$ 個を選んで、選ぶのみで列的な考えをしない…　${}_n{C}_{\mathrm{r 公式}}$

　順列と組み合わせの違いしっかり押さえましょう。それでは、実際の例で、

　　　nPr

　　　　まず委員長は10人の中から一人だから１０通り。
　　　　残りの副委員長は委員長を除いて９人の中から選ぶので10‐１=9で９通りです。
　　　　同様、書記は残り８人の中から１人選ぶので８通りですね。
　　　　よって10ｘ９ｘ８=720通り　になります。順列の簡単な公式があります。

　　　　10人の中から、それぞれ違った役員を３人を選ぶには₁₀Ｐ₃

　　　　この式はつまり10人（個/枚）の中から３人（個/枚）を１人（個/枚）ずつ選ぶ（取る）
　　　総数を計算する公式です。

　　　　　　10Ｐ3=10x9x8 = 720通りになります。　　　※Ｐはpermutationの頭文字

　♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪

　異なるｎ個のものから異なるｒ個を取り出す順列の総数は以下の式で表せます。
　
　　　　　　　　

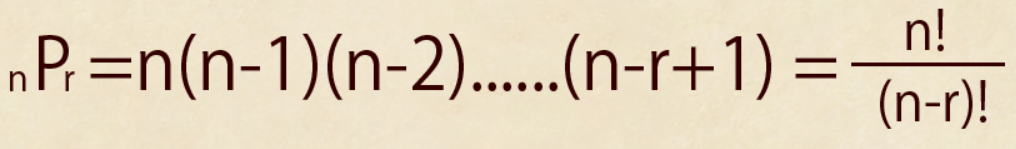
　　１番目の選び方はが、n通り　　２番目の選び方は、n-1通り　　３番目の選び方は、n-2通り
　　同様に・・　　　ｒ 番目の選び方は、n-r+1通り

　♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪

　　列の計算は カウントダウンのかけ算 。　つまり、

　　　「5人を1列に並べるなら5×4×3×2×1」　 5Ｐ5 　 5Ｐ5は　５!とも書きます。(！: かいじょう)
　　　「4人を1列に並べるなら4×3×2×1」　　 　 4Ｐ4 　同じく　４!
　　　「3人を1列に並べるなら3×2×1」　 　 　 　 3Ｐ3　 　　 　 　 ３!　 　

　　順列の計算は 数字が1つずつ減っていくかけ算になる ということですね。
　　簡単に考えると、カウントダウンだね。

　　　♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪

　異なる$n$個のものから $r$個を選んで、一列に並べる。${}_n{P}_r$　これが順列

　異なる$n$個のものから $r$個を選ぶのみ　　　　　　　　　${}_n{C}_{\mathrm{r これが組合せ}}$

　　順列と組合せ　ーー　しっかり区別しましょう。

　次の問いでの計算をやってみよう。

　　　(1) 5P2=5x4=20　　※5から-1ずつ２回掛けます
　　(2) 6P4=6x5x4x3=360

　　じゃあ、組み合わせは、どうだろう。以下、組合せについて学習しましょう。


　組合せについて簡単に説明しましょう。
　　　　　　　　　　
　　順列では、前例「10人の生徒の中から委員長、副委員長、書記の３人を１人ずつ選ぶ」でしたね。

　　いっぽう、組合せは選ぶだけで区別しないことです。組合せの問いでは、以下のようになります。

　　　　並べる順序、つまり３人の委員で委員長、副委員長、書記にこだわりません。

　　　　10Ｃ3 ＝(10×9×8）÷(3×２×１)=720/６=120通りになります。
　　　　　　　　　　　　　　　　　　　　　　　　　　※　Ｃ：combination


　　異なるｎ個のものから異なるｒ個を取る組み合わせの総数は以下の式で表せます。
　　　　　　

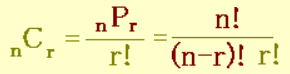
　　　　　　　　組み合わせの公式も、なんだか難しい計算式になってるようですね。
　　　　　　　　わからなくても、あまり気にしないこと。多くの問題を解くことで、すぐ慣れます。

　　次の問いで　の計算式に慣れましょう。

　　　　　(1) 5C2=(5×4)/(2×1)=10　 ※5から-1ずつ２回掛け、それを2×1で割ります
　　　　　　　　(2) 7Ｃ3=(7×6×5)/3×2x1=35

ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

　ふたたび順列に戻りましょう。
　　　　
　　　それでは必ずと言っていいほど出題傾向の高い問題をやってみよう‼。

　　　　　先頭に立つ並び方は４通りあり、１人決まったので残りの３人は３通りですね。

　　　　さらに残りの２人は２通り。積の法則から

　　　　４ｘ３ｘ２ｘ１=24通り。　 以下の計算式が成り立つ　⇒　４！=24 または　4Ｐ4=4x3x2x1=24

　　　　　考え方）　まず（１）の問いでは両端にくる男子に注目。
　　　　　　　　　　　

　　　　　　　　　　男子3人の中から両端にくる男子２人を選んで並べる方法は？　3Ｐ2=３ｘ２＝６通りですね。
　　　　　　①このそれぞれの場合について　残りの３人が１列に並ぶ並び方は

　　　　　　₃Ｐ₃=３ｘ２ｘ１＝６通り

　　　　　　②　①それぞれの場合についてだから積の法則でよって₃Ｐ₂ Ｘ ₃Ｐ₃=　３６通りです…答

　　　　　　　　～～～～～～～～～～～～

　　　　　（２）の問い　　　女子２人が隣り合う並び方は、女子２人をひとまとめにして１人として考えます。

　　　　　　　　　　　　…………

　　　　　　いずれにせよ、女子２人が隣り合っていれば良いのですから、

　　　　　　女子２人をひとまとめにして１人として考え、４人が１列に並ぶ並び方を考えます。

　　　　　　４人が１列に並ぶ並び方は4Ｐ4=4x3x2x1=24通り　　４！ですね。

　　　　　　このそれぞれの場合（積の法則）について、女子２人の並び方は2Ｐ2=2x1=2通り。

　　　　　　　よって並び方の総数はこのそれぞれの場合についてだから

　　　　　　　　　積の法則から　　２４ｘ２=48通り　…答

　たくさんの問題に挑戦して、問題に慣れましょう。

答　　(1)　男　女　女　男　男　男　　５！×２！＝２４０通り　　
　　　(2)　女　男　男　男　男　女
　　　　　　 両端の女子２人の並び方は２！　
　　　　　　また、この並び方のそれぞれに対して、そのあいだに４人の男子が並ぶ並び方は４！
　　　　　　よって　　２！×４！＝４８通り
　　　(3)　２！×３！＝１２通り

　

　中華料理を食べに行ったことがありますか。行ったことがなくても円卓に座って、
前に置いてある食べ物を、みんなで食べることを想像しましょう。

　ただ、「Aさんの人のそばがいい」とか「Bさんの横には座りたくない」など、
それぞれ思いがあるかと思います。しかし、そんな甘えたことは言っておれません。

　５人が円卓を囲むときの、並び方は何通りあるか、これが円順列です。
　
　まず、自分が　に座るとします。これで1人確定。残りは４人。

あとは以下のように隣から順に決めていけばいい。

帯状にしました。 　 　４人を一列に並べる。つまり、円順列も順列なのです。

　答　自分を。またはだれか一人を円卓のどこかに固定しますので、あとは①から④までを
　　　　１列に並べることになります。
　　　　よって　　4Ｐ4。　つまり　４！= 4x3x2x1 = 24通りになります。

　　異なるｎ個のものの円順列の総数は　　　（ｎー1）！　　で表せます。
　　しっかり覚えていてください。

　　　　　　（６－１）！= 5！ =5x4x3x2x1 =120通り

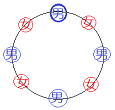
【解説】　男子が円形に並んで、あいだに女子が並んでいくと考えましょう。 男子が円形に並んでから特定の男子（太い丸）を基準にすると、あいだに入る女子の並び方は、 １列に並ぶ順列と考えられる。
男子だけを考えよう。特定の男子１人は固定して、男子４人の円順列の総数は(４－１)！通り 　そのどの場合に対しても女子４人が男子のあいだに１人ずつ並ぶ方法は４！ 　よって３！×４！＝１４４通り

　
　　　これまで異なるものだけを並べる順列を考えてきましたが、ここで、同じものを繰り返し使うことを許した場合の
　　順列について考えてみましょう。

6種類のジュースを売っている自動販売機があります。 　3人の子供が1人一本ずつ買うとき、何通りの買い方があるでしょう。但し、売り切れはないものとします。

　３人を仮にAくん、Bくん、Cくんとしましょう 
　Aくんの買い方は６通り。　同様にBくん、Cくんも６通り
　よって買い方の総数は、積の法則より、６ｘ６ｘ６ = ２１６通りになります

　答　３つの数から４個とる重複順列だから、一桁目３通り、２桁目も３通り…。よって、３×３×３×３＝８１
　　　　　　XXXX

　答　百の位はX通り、十の位はX通り、一の位はX通り。どの位についてもX通りずつの選び方があるので、
　　　積の法則により４×４×４＝６４個

　答　1回目２通り。２回目も同じく２通り…。　よって２×２×２×２＝１６通り

　　　　　(1)　Aに対して４通り。２個のどの文字列にも４×４＝１６

　　　　　(2)　Aに対して４通り。Bに対しても４通り。　３個のどの文字列にも　４×４×４＝６４

　　　nCr

　　順序を意識した順列に対し、ここでは並べる順序（例えばトップランナーやアンカー、
　または学級委員、副委員などを問題にせず、ランナーを何人、委員を何人などと）をいくつか、
　（いく人）の中から何個（何人）かを選んで組をつくるときの総数（組合せ）について考えます
　${}_{\mathrm{ｎ個のものからｒ個取る組合せ、その総数をnＣrで表します。\; ｎ個のものから順番、順序を決めてｒ個取る組合せの総数はnPr(順列)で表します。}}$
　　具体的に計算してみましょう。

　　　$①$$4C2=\; (4\times ３)\; /\; (2\times 1)$ =$6$
　　　　　　$4$$C$$2$　４から１つずつ、−して掛けていきます。$4C2$　なので２回まで。それを(２×１)で割ります。

　　　②　$9C3=\; (9\times 8\; \times 7)\; /\; (3\times 2\times 1)=$$84$
　　　　　　$9C3$　９から１つずつ、−して掛けていきます。
　　　　　　　$9C3$なので３回まで。それを（３×２×１）で割ります。
　　
　まず、実際の例題で考えてみましょう。　

答
$例１)$$4C2= (4\times 3)÷(2\times 1)\; =\; ６$$（通り）\; 罰ゲームが当たった２人は、Ａくん、Bくん２人としたらＡくん、\; Ｂくんのどちらかは問いませんので４人から２人を選ぶ組合せですね。\; 例２) 5C3= 10（通り）\; 例３) (1)$
$(2)男子３人から２人を選ぶ組合せ3C2通り。$　$女子４人から２人を選ぶ組合せ4C2通り\; よって、求める総数は3C2\times 4C2＝１８通り$　

　　　　$(3)$$問$男子３人、女子４人の合計７人のグループから４人を選ぶとき、
　　　　　　　　 必ずＡくん（男子）とＰさん(女子）が選ばれる選び方の問い。

$男子\; 3人、女子\; 4人の合計7人のグループから、4人を選ぶときで、\; 必ず、Aくん\; （男子）とPさん(女子）が選ばれる選び方は何通りかを問う問題で、$$４人のうち、２人はすでに選ばれているので、残りの$$２人の選ばれかたの総数を求めます。\; 全７人のうち、ＡとＰを除く５人から２人を選べばよいので、5C2＝10通り$　

■　${}_{\mathrm{nCr}}$の性質　　${}_{\mathrm{nCr\; =nCn-r}}$も成り立ちますp30

　　区別のある組分けと区別のない組分け

${}_{\mathrm{６人をそれぞれaくん,b,c,d,e,fくんの６人としよう。}}$${}_{\mathrm{【区別のある組分け】}}$${}_{\mathrm{例１ 答）}}$${}_{\mathrm{中学で樹形図を学習したので思い出してください。\; ａとｂ、ａとｃ、ａとｄ、ａとｅ、ａとｆ。 ｂとｃ、ｂとｄ\dots 等々の組に分けられます。\; ６人の中からＡ部屋に入る２人を選ぶ選び方は\; 6C2\; このそれぞれの場合について、残りの４人からＢに入る２人を選ぶ選び方は4C2\; 通り\; 最後に残った２人はＣ部屋に入るだけです。よって求める分け方の総数は 6C2\times \; 4C2\times 2C2=\; 90\; 通り}}$${}_{\mathrm{【区別のない組分け】}}$${}_{\mathrm{例２\; 答)\; \; (1)の90通りでＡＢＣ３つの部屋の区別をなくすと、同じ組み分けになるというのがキーポイント。\; 同じ組み分けになるものが３\times ２\times １。つまり３！なので\; 求める組み分けの総数は (1)の答え９０通りを３！で割ります。 １５（通り）\dots 答}}$
${}_{\mathrm{同じものを含む順列}}$

　　　　　　${}_{\mathrm{a,\; a,\; a,\; b,\; b,\; c,\; c}}$${}_{\mathrm{の７枚のカードすべてを１列に並べる並べ方の総数について考えよう。}}$

　　${}_{\mathrm{同じような例題で再度やってみよう。}}$

${}_{\mathrm{答}}$${}_{\mathrm{8Ｃ}}$_{${}_3$}${}_{\mathrm{\times }}$${}_5$${}_{\mathrm{C3\; \times }}$${}_2$${}_{\mathrm{C2\; =\; 560通り}}$

${}_{\mathrm{図3}}$

　　${}_{\mathrm{Ａ地点からＢ地点までの道順は３個の}}$${}_{\mathrm{\uparrow }}$${}_{\mathrm{と４個の}}$${}_{\mathrm{\to }}$${}_{\mathrm{を１列に並べたもので表すことができる。\; これは図３のような７個の場所のうち、３個に\uparrow 、４個に\to を入れて得られるが、\; \uparrow の入る３個の場所を決めれば、残り４個の場所に\to が入ることになる。\; したがって求める道順の総数は}}$${}_7$${}_{\mathrm{C}}$${}_3$${}_{\mathrm{=３５通りとなります。または ※}}$${}_7$${}_{\mathrm{C4 でも答えは同じですね。\; こう説明すると分かりやすいかな？}}$${}_{\mathrm{右に４区画、上に３区画の合わせて７区画の中から、\; 上に進む３区画ををどこにするか選べばＡ地点から\; Ｂ地点まで行く最短経路が１つ決まる。よって}}$${}_7$${}_{\mathrm{C3 = ３５通り}}$　　　　　　　　

${}_{\mathrm{どうしてもわからない場合は、簡単な図で考えてみよう\; 図から３通りってわかる。\; 3Ｃ2、または 3Ｃ1 のどちらでも３になります。}}$

${}_{\mathrm{さらに問題を解いて、問題に慣れよう。}}$

${}_{\mathrm{問２ 右のような道があるとき、次の場合の遠回りしないで行く道順は何通りありますか。\; (1)\; A地点からＢ地点まで行く。\; (2)\; Ａ地点からＣ地点まで行く。\; (3)\; A地点からＣ地点を通ってＢ地点まで行く。}}$

${}_{\mathrm{(1)縦４画、横４区画}}$${}_8$${}_{\mathrm{Ｃ}}$${}_4$${}_{\mathrm{=(8\times 7\times 6\times 5)/(4\times 3\times 2\times 1) =70通り\; (2）4Ｃ2}}$${}_{\mathrm{=\; ６通り \; (3) (2)より A～C=6通り。\; それぞれに対しC～Bも６通り。積の法則より６\times ６=３６通り}}$

問３ 以下、何通りありますか 　(1) A地点からC地点まで行く道順。 　(2)A地点からB地点まで行く道順 　(3) AからＢを通ってＣまで行く道順。

${}_{\mathrm{(1)\; 9C4でも9Ｃ5でも結果は同じ。 答 126通り\; (2)\; 5Ｃ３＝１０通り\; (3)\; ６０通り}$ {}_{}$}$

■組合せ　繰返し問題

(１)　${}_{\mathrm{5C3 ＝}}$１０通り

　　　${}_{\mathrm{12C3}}$ = ２２０　　１２個の点から3個選ぶと３角形ができる。

(1)　1260通り　

(2)　少なくとも1人はＡ組の委員なので（余事象）、「Ａ組の委員が入らない」を考え、すべての場合の数から引きます。
　　　　すべての場合の数は１８人から４人選ぶので、18Ｃ4 = ３０６０通り
　　　　「Ａ組の委員が入らない」場合の数は8Ｃ4 = ７０通り　なので　18Ｃ4－8Ｃ4 = ３０６０−７０＝２９９０通り

　(1)　絵札を2枚だけ取り出す ３枚ある絵札から２枚を取り出す場合の数が 3Ｃ2 = 3通り
　「10枚ある絵札以外のカード」から３枚を取り出す場合の数が 10Ｃ3 = １２０通り
　 この2つが同時に起こればいいので、求める場合の数は 3×120 = ３６０通り となります。

(2) 少なくとも1枚は絵札を取り出す余事象なので、「絵札を1枚も取り出さない」を考え、すべての場合の数から引きます。
　絵札を1枚も取り出さない場合の数は、10枚ある絵札以外のカードから5枚を選ぶ 10Ｃ5 = ２５２通り
　全ての場合の数は、13枚から5枚を選ぶ 13Ｃ5 = １２８７通り
　よって、求める場合の数は 1287-252 = １０３５ 通り となります。

　　①から⑥までの中から平行四辺形のための２本、ａ～ｄの４本の中から２本選ぶと平行四辺形が１つできる。
　　よって、平行四辺形の個数は、積の法則により、
　　　　6Ｃ2×4Ｃ2 = 90個

　　(1)　3Ｃ2 = ３個　　　　　　(2)　3Ｃ2 × 4Ｃ2 =１８個

${}_{\mathrm{問(53) 右図のような区画された道路がある。Ａ地点からＢ地点への最短経路は何通りあるか？}}$

　7Ｃ3 =３５通り

　(1)まずＡの箱は 8Ｃ2　　Ｂの箱は残りの６個から入れるので　6C2
　　　同様に考えて　8Ｃ2×6C2×4C2×2C2 =２５２０　２５２０通り…答

　(2)　箱に区別がないので（ ２個ずつを４箱に入れるので)
　　　入れ方が４！＝２４通りずつ重複します。よって、 （１）で求めた２５２０通りを ４！＝２４で割ります。
　　　　　　　２５２０÷４！＝１０５通り…答

問(55) 　(1) AからＢへの最短経路は何通りありますか。 　(2) AからＣを通らないでＢへ最短経路で行く道順は何通りありますか。

　${}_{\mathrm{(1)\; 8Ｃ３＝５６通り}}$
${}_{$ {}_{\mathrm{(２)\; 反対に、Cを通る道順は \; 3Ｃ２\times ５Ｃ２＝３０通り \; よって、Cを通らない道順は５６－３０＝２６通り}}$}$

(1) 3つのセットは個数がそれぞれ異なり、すでに区別がついているので、順に選んでいけばいいですね。
　　　 　 10Ｃ2×8C3×5C5 = 2520通り…答

(2) このときは3個入りのセットが2つあるので上の方法で数えたあと、2つの区別をなくせばいいんですね。
　　2つの区別をなくす。つまり２！＝２で割ります。
　　　　　　　　 (10Ｃ3×7C3×4C4 ) / 2！ =2100通り…答

　(1)　6Ｃ3×3C1×2C2 =６０個

　(2) 偶数になるには下１桁に２がくる場合だけなので、　6Ｃ3×2C2 =２０個

　　　答　(1) 60　　(2) 10

全部で表か裏 が３枚なので、 ２×２×２＝８通り。 これを念頭におきます。
　(1) （表、表、表）の出方で１通り。 よって８分の１です。
　(2) 　２枚表が出るというと(表表裏)、(表裏表)、(裏表表)の3通りなので、８分の３になります。
　(3) 「少なくとも１枚表」ということは、 全部が裏でさえなければ、成り立ちますね。
　　　よって、全体の場合の数から、全部が裏の場合を引けばいいです。 全部が裏の時は、一つ目と同じ考え方で、１通りです。
　　　よって、８分の（８−１）より、８分の７です。　　※　樹形図を書いてもいいね。

　　(１)1/6 　　　(2)5/12

　(1) 大きいほうのさいころを左辺に書く
　　　　１－４　　　４－１
　　　　２－５　　　５－２
　　　　３－６　　　６－３　　　の６通りなので　６/36 　１/６

　(2) 1/2

　(3)　大小２つのサイコロの目の出方の総数＝目の積が３の倍数となる場合の数＋目の積が３の倍数とならない場合の数という関係を利用しましょう。

　　　　・大小２つのサイコロの目の出方の総数=6x6=36通り　　・目の積が３の倍数とならない場合の数=4x4=16通り
　　　　　　　　(↑大小共に、目が３，６以外なら目の積は3の倍数とならないから）

　　　　　よって、目の積が３の倍数となる場合の数=大小２つのサイコロの目の出方の総数-目の積が３の倍数とならない場合の数
　　　　　　　　３６－１６　＝２０　通りなので　２０/３６= ５/９　　　　　　５/９…答

　図を書いて解く方法もありますね。

目の積が3の倍数になるということは、大中小のさいころの少なくとも1つが3の倍数(つまり、3か6)になるということ。
このように「少なくとも1つが…」という問題は、「全体の場合の数から、そうならない場合の数を引き算する」という方法が便利。
(確率の問題で言う、「余事象」の活用)

まず、全体で何通りあるかを計算すると、6×6×6=216通り。
「少なくとも1つが3の倍数になる」ということにならないのは、「3つのさいころの目が、1、2、4、5の4種類のいずれか」ということ。
この場合の数は、4×4×4=64通り。
したがって、求める場合の数は、216-64=152通り。

３個のサイコロを投げると目の出方は全部で６の３乗＝２１６通り
３個のサイコロを投げて、出る目の和が５になる組み合わせは （1、2、2）（１、1、3）のいずれかで、
（１，２，２）のとき目の出方は３通り 。（1，1，3）のときも目の出方も３通り。よって、
目の和が５になる場合は全部で６通り。 したがって、出る目の和が５になる確率は　６÷２１６＝１/３６です。

　　総合問題　　　　　簡単な問題になんどもチャレンジし、コツを学び取りましょう。

${}_{\mathrm{集合の要素の個数を問う問題です。}}$${}_{\mathrm{答）(1) ｎ(A)=20 (2)\; n(B)=15 (3) n(Ā)=40 \; (4)\; ｎ(A\cap B)=5 (5)n(A\cup B)=30 \; (6)\; =15}}$${}_{\mathrm{(1)\; 集合A=｛３,６,９,12,15,18,\; 21,24,27,30.33.36.39,42,45,48,51,54,57,60｝n(A)=20\; (2)\; 集合B=｛4,8,12,16,20,24,28,32,36,40,44,48,52,56,60｝n(B)=15}}$　　(1)、(2)は単に60÷3=20　　60÷4=15 で計算してもOK。ｎ(Ā)=n(U)-n(a)=60ー20=40

　　(4) (A∩B)={12,24,36,48,60}よりｎ(Ａ∩Ｂ）=5

　　(5) ｎ(A∪B)= n(A)+n(B)－ｎ(Ａ∩Ｂ）より20+15－５=3０

　　(6)${}_{\mathrm{＝｛1,2,3,5,6,7,9,10,11,13,14,15}}$${}_{\mathrm{,}}$${}_{\mathrm{17,}}$${}_{18}$${}_{\mathrm{,19,}}$${}_{21}$${}_{\mathrm{,22,23,25,26,}}$${}_{27}$${}_{\mathrm{,29,}}$${}_{30}$${}_{\mathrm{,31,}}$${}_{33}$${}_{\mathrm{,34,35,37,38,}}$${}_{39}$${}_{\mathrm{,41,}}$${}_{42}$${}_{\mathrm{,43,}}$${}_{45}$${}_{\mathrm{,46,47,49,50,}}$${}_{51}$${}_{\mathrm{,53,}}$${}_{54}$${}_{\mathrm{,55,}}$${}_{57}$${}_{\mathrm{,58,59｝\; 赤の数字が集合Ａと重なった数字で15個}}$

${}_{\mathrm{答）(1)９通り}}$

${}_{\mathrm{(2)\; 12通り}}$${}_{\mathrm{いずれも和の法則ですね}}$

　　　${}_{\mathrm{①\; は順列で}}$${}_{20}$${}_{\mathrm{P}}$${}_3$${}_{\mathrm{=\; 6840通り \; ②は組合せ 20C3＝(20\times 19\times 18)/(3\times 2\times 1)=1140通り}}$

${}_{\mathrm{まずは隣り合う女性２人をひとかたまり６人として考えると６！になり、\; 次に女子2人の並べ方は２！なので積の法則から６！\times ２！=1440\; 通り}}$

${}_{\mathrm{両端の女子２人の並び方は2Ｐ2=\; 2！通り\; この並び方それぞれに対してその間に男子５人が並ぶ並び方は 5Ｐ5=\; ５！\; よって求める並び方の総数は、積の法則より2！\times ５！＝２４０通り}}$

${}_{\mathrm{０を除くと1桁に与える数字は10－1\; =\; 9通り\; 同じ数字も使えるので次の桁も９通り、同様に９通り。 積の法則より ９\times ９\times ９=\; 729\; 通り}}$

　円順列ですね。（nー1）！より24通り

　本問題は順列かな？　　　　２８通り

　　　　105通り