「ＡとＢの共通部分」といい「ＡかつＢ」で集合ＡとＢの重なった部分の集合
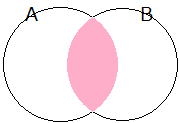
「ＡまたはＢ」で集合ＡとＢの要素すべて
１節 集合と論証 戻る
１ 集合
| Ａ∩Ｂ 共通部分 「ＡとＢの共通部分」といい「ＡかつＢ」で集合ＡとＢの重なった部分の集合 |
|
| Ａ∪Ｂ 和集合 「ＡまたはＢ」で集合ＡとＢの要素すべて |
|
具体的に説明しましょう。
Ａ＝｛１,３,５,７,９} Ｂ= ｛３,４,５,６｝について、
Ａ∩Ｂ（共通部分） Ａ∪Ｂ（和集合）は？
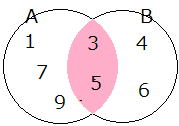※Ａ，Ｂの、まず共通部分から見ていきましょう
集合の表し方
集合を表すにはＡ＝｛１,３,５,７,９}以外に次の方法があります。
Ａ=｛Ｘ｜Ｘは10以下の正の奇数｝
例）Ａ=｛Ｘ｜Ｘ2= ９｝のとき Ａ=｛３，－３｝
| 問）次の集合を、要素をかき並べる方法で表せ。 (1) Ａ=｛Ｘ｜－１≦Ｘ≦２, Ｘは整数｝ (2) Ａ=｛Ｘ｜Ｘは１０以下の正の奇数｝ (3) Ａ=｛Ｘ｜－３＜Ｘ＜１, Ｘは整数｝ |
答）(1) Ａ=｛－１，０，１，２｝
(2) Ａ=｛１,３,５,７,９｝ (3) Ａ=｛－２,－１，０｝
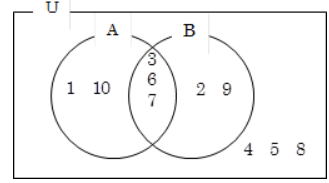
例題１） Uは全体集合 |
| 例題２） Ａ={X| -2<X<3, Xは実数｝、B={X| 0<X<5, Xは実数｝のとき、A∩B およびA∪Bを求めよ。 |
答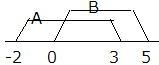 
A∩B＝｛１,２｝ A∪B＝｛－１,０,１,２,３,４｝
| 例題３） Ａ={X| １≦X≦５, Xは実数｝、B={X| ３≦X≦７, Xは実数｝のとき、A∩B およびA∪Bを求めよ。 |
補集合とド・モルガンの法則
| 例題１）U={１,２,３,４,５,６,７,８,９｝を全体集合とするとき、その部分集合 A=｛２,３,５,７｝、B=｛１,３,５,７,９｝について、次の集合を求めよ。 (１)  (２)  (３)  (４)  (５)  (６)  |
まずＡ，Ｂの共通要素から考えましょう
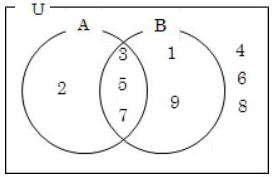
答 (１)
＝｛１,４,６,８,９｝
(２) 
=｛３,５,７｝より =｛１,２,４,６,８,９｝
(３) (1)の要素と
=｛２,４,６,８｝から＝｛１,２,４,６,８,９｝
(4) ={１,９} (５) =｛４,６,８｝ (６) =｛４,６,８｝
ここで前問の(５)(６)の結果が等しいのに注目しよう。
=｛４,６,８｝ (６) =｛４,６,８｝つまり、
① = ② 
= 
これが、ド・モルガンの法則です。
ベン図を書いて考えましょう。
①は
②は
例題２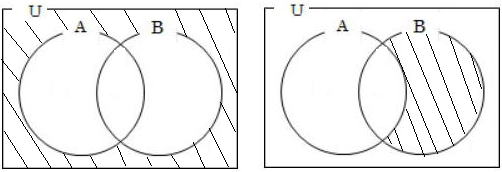） ベン図(１) ベン図(２) 上のベン図は以下の集合（全体集合をＵとする。）のいずれを表しているか。 記号で答えよ。  ベン図(１)は（ と ）ベン図(２)は（ ） |
ベン図(１)はまず⑥、⑥からド・モルガンの法則により⑤を導くのが楽ですね。
ベン図(１)は（ ⑤と⑥ ）ベン図(２)は（ ④ ）
２命題の真偽と集合
正しいか正しくないかが定まる文や式を命題という。
命題が正しいとき、その命題は真であるという。
命題が正しくないとき、その命題は偽であるという。
それでは以下の命題はの真偽は？
① X=１ならば、X2=１である。
②Xが偶数ならばXは４の倍数である。
③１００００は大きい数である。
どうだろうか？①は真、②は偽の命題ですね。
③は正しいか正しくないか決められないので命題とはいえません。
| 例１）ｐ： －１＜X＜２、ｑ：－２＜X＜４として、命題「ｐ⇒ｑ」の真偽を確かめてみよう。ただしXは実数とする。 条件ｐ、ｑを満たすXの集合をそれぞれＰ、Ｑとする。このとき下図から  が成り立つ。よって、命題「ｐ⇒ｑ」は真である。 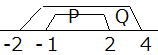 命題「ｐ⇒ｑ」が偽であることを示すには、 「ｐを満たしているがｑを満たしていない」という例を １つあげればいい。このような例を反例という。 |
| 例２）ｐ： －１＜X＜２、ｑ：０＜X＜４のとき、命題「ｐ⇒ｑ」は 偽であることを示してみよう。ただしXは実数とする。 下図から  はｐを満たしているがｑを満たしていない。よって、 は反例であり、命題「ｐ⇒ｑ」は偽である。  |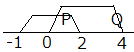
| 練習 次の条件ｐ，ｑについて、命題「ｐ⇒ｑ」の真偽を答えよ。 また、偽の場合は反例をあげよ。ただしXは実数とする。 (1) ｐ：ｎは４の正の約数 ｑ： ｎは12の正の約数 (2) ｐ：１＜X＜４ ｑ：１＜X＜２ (3) ｐ： X＜ー３ ｑ： X＜ －２ |
(1)「ｐ⇒ｑ」は偽 反例：X=４ または８
(2)「ｐ⇒ｑ」は真 (3) 「ｐ⇒ｑ」は偽 反例：
必要条件と十分条件
命題「Xが６の倍数ならばXは３の倍数である」は真である。
よって、ある数Xが３の倍数であるためには、６の倍数であれば十分である。
また、ある数Xが６の倍数であるためには、３の倍数であることが必要である。
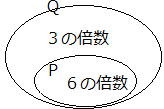命題「ｐ⇒ｑ」が真であるとき、
ｐはｑであるための十分条件である。
ｑはｐであるための必要条件である
例１）２つの条件
ｐ：△ABCは正三角形
ｑ：△ABCは二等辺三角形 について、命題「ｐ⇒ｑ」は真か偽か。
正三角形なら二等辺三角形はいえるから、命題「ｐ⇒ｑ」は真。 よって、
ｐはｑであるための十分条件である。ｑはｐであるための必要条件である。
※ 命題「ｐ⇒ｑ」が真であることは、となることと同じである。
命題「ｐ⇒ｑ」と命題「ｑ⇒ｐ」がともに真であるとき、
ｐはｑであるための必要十分条件である。という。また、このとき
ｑはｐであるための必要十分条件でもある。 ｐ⇔ｑで表す。
３ 命題と証明
逆と対偶
命題「ｐ⇒ｑ」に対して「ｑ⇒ｐ」をもとの命題の逆という。
命題「Ｘ＞５⇒Ｘ＞２」は真だが、その逆は「Ｘ＞２⇒Ｘ＞５」となり
偽である。もとの命題が真であっても、その逆が真とは限らない。
| 問）次の命題の逆をつくり、その真偽を調べなさい。 (１) nが自然数のとき、 nは４の倍数 ⇒ nは２の倍数 (２) Ｘ＝３ ⇒ ４Ｘ－１２=０ |
(１) もとの命題は真である。逆にすると、
ｎは２の倍数 ⇒ ｎは４の倍数 偽である。
(２) もとの命題は真である。逆にすると、
４x－１２=０ ⇒ x＝３ 真である。
対偶とは
命題「ｐ⇒ｑ」に対して 
をもとの命題の対偶という。
| 「ｐ⇒ｑ」← 逆 →「ｑ⇒ｐ」 「ｐ⇒ｑ」←対偶→ |
例）次の命題の逆、対偶をつくりなさい。
(1) nが自然数のとき
nは４の倍数 ⇒ nは偶数
逆： nは偶数 ⇒ nは４の倍数
対偶：nは奇数 ⇒ nは４の倍数でない
(2) x =８ ⇒ x2=６４
逆： x2=６４ ⇒ x =８
対偶：x2≠６４ ⇒ x ≠８
| 問）次の命題の対偶をつくりなさい。 (1) nが自然数のとき nは１０の倍数 ⇒ nは５の倍数 (2) x ＞３ ⇒ x2＞ ９ (3) x2 ≦ １６ ⇒ x ≦４ |
答）(1) nは５の倍数でない ⇒ nは１０の倍数でない
(2) x2 ≦９ ⇒ x ≦３
(3) x ＞４ ⇒ x2 ＞１６
| 命題が真ならば、その対偶も真である。また、対偶が真ならば、もとの命題も真である。 |  |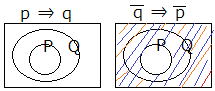
-------------------------------------------------
ｎが自然数のとき、次の命題を証明する。
命題「n2は奇数 ⇒nは奇数」
---------------------------------------------------------
証明）与えられた命題の対偶「nは偶数 ⇒n2は偶数」が真であることを証明する。
nを正の偶数とすると、mを自然数として、nは偶数だからn=２mと表せる。
よって、n2=（２m)2 = ２×２m2
２ｍ2は自然数であるから、n2は偶数である。よって、
「nは偶数 ⇒n2は偶数」は真である。したがって、
対偶が真であることが証明されたので、もとの命題も真である。
| まとめ問題 (1) 次の集合を要素を書き並べて表せ。 ① ６の正の約数の集合Ａ ② １以上２０以下の６の倍数の集合Ｂ (2) 次の命題の真偽を調べ、偽である場合は反例をあげよ。 ① x=６ ⇒ x2 = ３６ ② x2 = １６ ⇒ x=４ ③ －３≦x≦１ ⇒ －５＜x＜－２ ④ －２＜x＜－１ ⇒ －６＜x＜０ (3) 次の条件の否定を述べよ。 ① xは有理数である。 ② x≦４ ③x＜５ ④x≧－２ (4) 次の（ ）の中に「必要」「十分」「必要十分」のいずれか あてはまるものを答えよ。 ① x2 = ９はx=－３であるための（ ）条件である。 ② x=１はx2 = １であるための（ ）条件である ③ x2 = 36 はx=６であるための（ ）条件である。 ④ x＞１ はx＞２ であるための（ ）条件である。 |
答）(1) ① Ａ=｛1,2,3,6｝ ② B=｛6,12,18｝
(2) ① 真 ② 偽 反例：x=－１
③ 偽 反例：x=－４ ④ 真
(3) ① Ｘは無理数である ② x>4 ③ x≧5 ④ x<－2
(4)