目次 福岡県入試過去問 31年問題 2学期期末テスト
| 単元1 運動とエネルギー | 単元4 化学変化とイオン 1章 水溶液とイオン 2章 化学変化と電池 3章 酸・アルカリとイオン |
| 単元2 生命のつながり 1章 生物の成長とふえ方 2章 遺伝の規則性と遺伝子 |
単元5 地球と宇宙 (kita9.ed.jp) |
| 単元3 自然界のつながり 1章 生物どおしのつながり 2章 自然界を循環する物質 |
単元6 地球の明るい未来のために |
復習
| 問 ① 秒速10mは分速何mか。 ② 分速50mは時速何kmか。 ③ 時速30kmは分速何mか。 ④ 時速90kmは秒速何mか |
答 分速600m 時速3km 分速500m 秒速25m
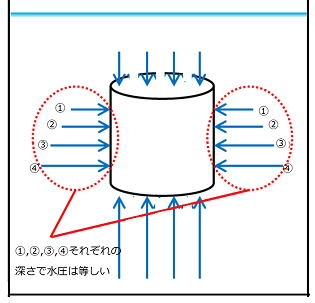
| 浮力 左図のように、物体にはたらく水圧のうち、側面にはたらくものは水深が同じであれば大きさは同じなので互いに打ち消し合います。 次に上面にはたらく水圧と下面にはたらく水圧を比べると、水深が大きい分、下面にはたらく水圧の方が大きくなります。 下面にはたらく水圧と上面にはたらく水圧の差から物体には上向きに力がはたらくことになります。 このように水圧の差から生じる上向きの力を浮力といいます。 |
 |
■単元1 運動とエネルギー
▲力の合成
・F1とF2の和が合力 ![]()
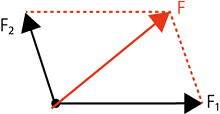
・F1とF2の差が合力 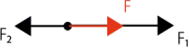
問 以下の図1,図2にF1,F2の合力を図示しなさい。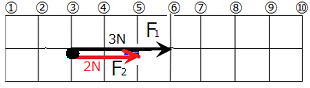 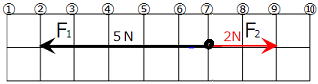 図1 図2 |
▲力の分解
・F1とF2が分力 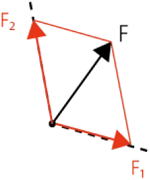
| 問 2つの力F1,F2を合成した力Fを以下の解答用紙に矢印で表しなさい。
|
解答
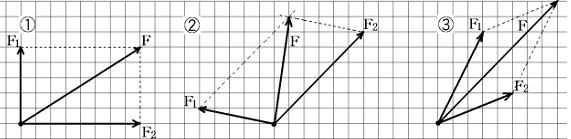
| 問 次の( )にあてはまる語句を答えなさい。 ・物体にはたらく2つの力の1つの力に置きかえる力のことを力の合成といい、 求めた力を ( ① ) という。 一直線上にない2力の ①は、2力を二辺とする平行四辺形の ( ② ) で表せる。 |
答 ① 合力 ② 対角線
| 床や机など水平な面に物体を置いた場合、物体に働く重力と抗力(垂直抗力)がつりあっている。 抗力とは変形した床や机の面がもとにもどろうとする力である。 作用点に注意! |
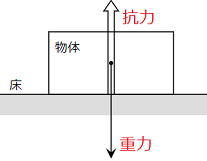 |
水平面に置いてある物体を動かそうと力を加えても動かない場合、物体を動かそうとする力と摩擦力がつりあっている。 摩擦力とは物体どうしがふれあっているとき、運動しようとする向きと反対の方向にはたらく力である。 作用点に注意! |
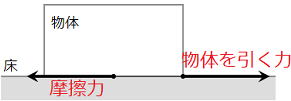 |
つり合う力の条件
①2力は同じ大きさである。
②2力の向きが反対である。
③2力は同一直線上にある
・物体に2力がはたらいていて、物体が静止している場合、
これらの2力は(つりあっている)という。
・床や机など水平な面に物体を置いた場合、物体に働く重力と(抗力/垂直抗力)がつりあっている。
・抗力とは変形した床や机の面が(もとに戻ろう)とする力である。
・水平面に置いてある物体を動かそうと力を加えても動かない場合、
物体を動かそうとする力と(摩擦力)がつりあっている。
・摩擦力とは物体どうしがふれあっているとき、
運動しようとする向きと(反対の)方向にはたらく力である。
・2つの力と同じはたらきの1つの力をもとの2力の(合力)という。
合力を求めることを力の(合成)という。
・一直線上ではたらく2力を合成する場合、同じ方向なら(和)、
反対方向なら綱引きのように(差)になる。
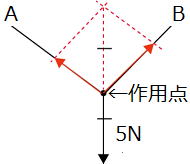
| 問 ①右図のように500gのおもりが天井からつるされています。 このときAの糸とBの糸がおもりを引く力を作図しなさい。 ただし、1nを1㎝とする。 ②右図の作用点の位置が間違っています。訂正しなさい。 (パソコン上で1㎝を測るのはほぼ不可能なので、おおよそでOKです。 ただし、テストのときは5Nが1㎝であることが求められます。) |
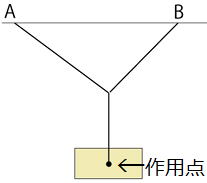 |
| 問 力について、次の各問いに答えなさい。 同じ作用線上にはたらく次の①,②の2力の合力の、向きと大きさをそれぞれ答えなさい。 ①右向きに6.0Nの力と、右向きに2.0Nの力 ( )向きに( )Nの力がはたらく ②右向きに3.0Nの力と、左向きに5.0Nの力 ( )向きに( )Nの力がはたらく |
①( )向きに( )Nの力がはたらく
②( )向きに( )Nの力がはたらく
| 問 物体にはたらく力がつりあうには、次の3つの条件を満たす必要がある。 ( )にあてはまる言葉を答えなさい。 ・2力の向きが( ) ・2力の大きさが( ) ・2力は( )ではたらく。 |
物体にはたらく力がつりあうには、
・2力の向きが(反対)
・2力の大きさが(等しい)
・2力は(一直線上)ではたらく。※「同一線上」、「同一作用線上」でも可
| 問 右図の①~④で2力がつりあっているものには〇を、つりあっていないものには欠けている条件をア~ウから選び、記号で答えよ。 ア. 2力が同じ作用線上にある。 イ. 2力の向きが反対 ウ. 2力の大きさが等しい |
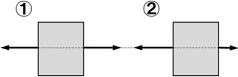 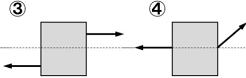 |
答 ①が〇 ②ウ ③ア ④イ
▲斜面上の物体
下の図はしっかり理解しよう。テストに度々出題されます。
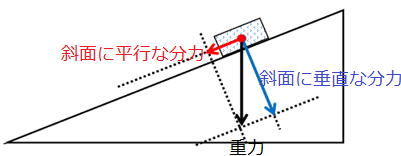
| 問 右図は斜面に置いた物体にはたらく重力を表している。この重力を斜面に垂直な方向の分力と、斜面に平行な方向の分力に分解せよ。 |
 |
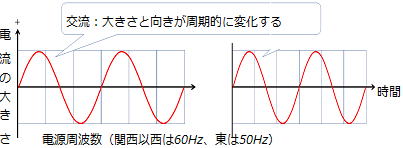
| 問 カッコ内に適切な語句または数字を入れよ。 (1)運動のようすを表すには( )と運動の( )を正確に示す必要がある。 (2) 速さの公式 速さ= (3) 物体がある時間の間、同じ速さで動き続けたと考えた時の速さを( )という。 (4) (3)において、ごく短い時間に移動した距離での速さを( )という。 (5) 一定の時間間隔でテープに点が打たれる装置を( )という。 (6) (5)は東日本では1秒間に( )回、西日本では1秒間に( )回のものが多い。 (7) 1秒間に60回打点する場合、( )打点で0.1秒である。 (8) 物体が真下に落下するときの運動を( )という。 (9) 斜面上の台車にはたらく重力は斜面に垂直な分力と、斜面に平行な分力に分解される。 ①斜面に垂直な分力は斜面からの( )とつり合う。 ②斜面に平行な分力は斜面の傾きが( )いほど大きくなる。 (10) 台車が斜面を下りる運動では、 ①斜面に平行で下向きの一定の力が加わるため速さがしだいに( )なる。 ②斜面の傾きが大きくなると速さの( )が大きくなる。 (11) 摩擦のある水平面では ①物体の運動の向きと( )向きに摩擦力がはたらく。 ②物体の速さはしだいに( )なる。 |
答(1) 運動のようすを表すには(速さ)と運動の(向き)を正確に示す必要がある。(2) 速さの公式
速さ=![]()
(3) 物体がある時間の間、同じ速さで動き続けたと考えた時の速さを(平均の速さ)という。
(4) (3)において、ごく短い時間に移動した距離での速さを(瞬間の速さ)という。
(5) 一定の時間間隔でテープに点が打たれる装置を(記録タイマー)という。
(6) (5)は東日本では1秒間に(50)回、西日本では1秒間に(60)回のものが多い。
(7) 1秒間に60回打点する場合、(6)打点で0.1秒である。
(8) 物体が真下に落下するときの運動を(自由落下)という。
(9) 斜面上の台車にはたらく重力は斜面に垂直な分力と、斜面に平行な分力に分解される。
①斜面に垂直な分力は斜面からの(垂直抗力)とつり合う。
②斜面に平行な分力は斜面の傾きが(大きい)いほど大きくなる。
(10) 台車が斜面を下りる運動では、
①斜面に平行で下向きの一定の力が加わるため速さがしだいに(大きく)なる。
②斜面の傾きが大きくなると速さの【ふえ方(変化する割合)】が大きくなる。
(11) 摩擦のある水平面では
①物体の運動の向きと(反対)向きに摩擦力がはたらく。
②物体の速さはしだいに(小さく)なる。
一直線上にない2力を合成する場合、2力を2辺とする(平行四辺形の対角線)が2力の合力になる。
1つの力を2つに分けることを力の(分解)という。
分けられてできた2力を(分力)といい、この2力でもとの1つの力と同じはたらきになる。
力の分解はもとの力を対角線とする平行四辺形の(2辺)が分力となる。
対角線から平行四辺形をつくる場合、辺の角度を変えることで何通りもできるので、
力の分解は分力の(方向)によって何通りもできる。
■記録タイマー
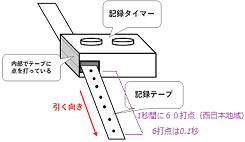
記録タイマーなどの問題をやるまえに、数学トレーニングしよう。
これができたらこれからの問いは簡単です。
たとえば、10㎝を0.1秒で動く物体の速度は100㎝/s。(s:Second,秒)。それでは、
200cm 10秒 20cm/s
①20㎝を0.1秒で動く物体の速度は(200 )㎝/秒。
②20㎝を0.2秒で動く物体の速度は(100 )㎝/s。
20÷0.2=200÷2=100㎝/s
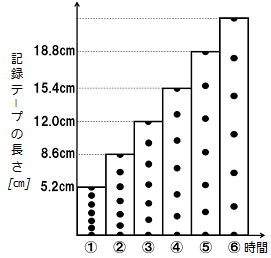
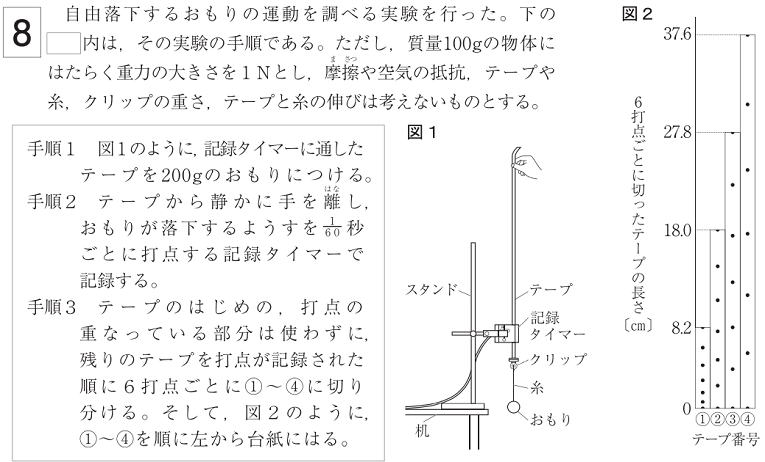
| 問 右図は1秒間に60回打点する記録タイマーの記録テープを、 6打点ごとに切って左から順に並べたものである。 ①記録テープ①を記録したときの台車の速さは何㎝/sか。 ②右図で記録テープ②を記録したときの台車の平均の速さは何㎝/sか。 ③右図で記録テープ③から④を記録したときの台車の平均の速さは何㎝/sか。 ④右図で記録テープ①から⑤を記録したときの台車の平均の速さは何㎝/sか。 ⑤右図に示した部分の記録テープ⑥の長さは何㎝であると考えられるか。 |
 |
解説と答
| ①記録テープ①を記録したときの台車の速さは何㎝/sか。 1秒間に60回打点する記録タイマーの6打点間の時間は0.1秒 よって52㎝/s 52㎝/秒でもOK ②右図で記録テープ②を記録したときの台車の平均の速さは何㎝/sか。 1秒間で8.6×10=86㎝/s 86㎝/秒でもOK ③右図で記録テープ③から④を記録したときの台車の平均の速さは何㎝/sか。 12.0㎝+15.4㎝=27.4㎝ 2本分なので (27.4×10)÷2=137㎝/s ④右図で記録テープ①から⑤を記録したときの台車の平均の速さは何㎝/sか。 ①から⑤までの長さは[ ]㎝なので ([ ]×10)÷5=120㎝/s ⑤右図に示した部分の記録テープ⑥の長さは何㎝であると考えられるか。 テープの長さは0.1秒ごとに3.4㎝長くなっていくので22.2㎝ |
 |
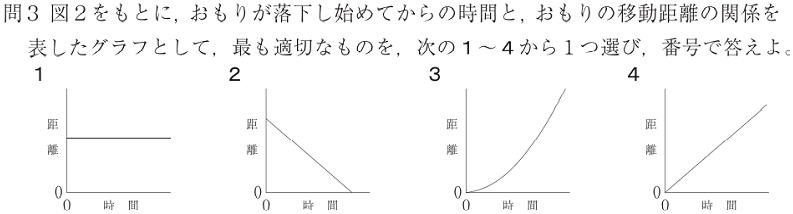
| 問 右の図は、0.1秒ごとに発光するストロボスコープで、小球の運動の様子を撮影したものである。各問いに答えよ。 (1) ア~イ間の小球の平均の速さは何㎝/sか。 (2) ア~ウ間の小球の平均の速さは何㎝/sか。 (3) ウ~カ間の小球の平均の速さは何㎝/sか。 (4) ア~カ間の小球の平均の速さは何㎝/sか。 (5)小球の平均の速さは0.1秒ごとに何㎝/s ずつ速くなっているか。 |
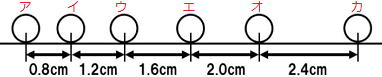 |
答 (1)8㎝ (2)20㎝ (3)60㎝ (4)80㎝ (5)0.4㎝
福岡県入試問題

答 
| (1) ア~イ間の小球の平均の速さは何㎝/sか。 0.8×10=8.0㎝/s (2) ア~ウ間の小球の平均の速さは何㎝/sか。 0.8+1.2=2㎝ 2㎝を0.2秒で動いているので2×5=10.0㎝/s (3) ウ~カ間の小球の平均の速さは何㎝/sか。 1.68+2.0+2.4=6.0㎝ 6.0㎝を0.3秒で動いているので6×10/3=20㎝/s (4) ア~カ間の小球の平均の速さは何㎝/sか。 トータルの長さ8.0㎝ 0.5秒で動いているので 8×2=20㎝/s (5)小球の平均の速さは0.1秒ごとに何㎝/sずつ速くなっているか。 ア~イ間の速さ:8cm、イ~ウ間の速さ:12cm、 ウ~エ間の速さ:16cmと、4cmずつ速さが増加してい ます。 4.0㎝/s |
 |
・等速直線運動
一定の速さで一直線上を動く運動を(等速直線運動)という。
等速直線運動をするのは、物体に力が(はたらいていない)ときや、
はたらいている力が(つりあっている)ときである。
・慣性
静止している物体が静止し続けようとする。
また、動いている物体が動き続けようとする性質を(慣性)という。
・作用・反作用
力は常に2つの物体の間で
この2力は同じ(大きさ)で(反対)向き、(一直線)上ではたらく。
この法則を(作用・反作用の法則)という。
(1 学期期末)
| 問1 次の文章中の①~⑤に適語を入れよ。 物体に力がはたらかないとき(または, 力が( ① )いるとき),物体はその運動の 状態を続けようとする性質がある。この性質を( ② )という。 イギリスの科 学者,ニュートンは,次のようにまとめた。 「他の物体から力が働かない場合,または,力が(①)いる場合に, はじめ静止していた物体はいつまでも( ③ )し,運動していた物体は そのままの速さで ( ④ )運動を続ける。」これを(②)の法則という。 |
[解答]① つり合って ② 慣性 ③ 静止 ④ 等速直線
| 問2 右の図はだるま落 としで,X の木片を 矢印の向きにすばや く打ち出した瞬間の 様子である。 (1) この後,X の上にある緑の木片はどうな
るか。次の[ ]から1 つ選べ。 [ 矢印の向きに動く 矢印と逆向きに動く 真下に落ちる ] (2) (1)の現象は物体がもつ何という性質 のためか。 |
 |
[解答](1) 真下に落ちる (2) 慣性
図のようにFでCを強くたたいてやると, C は左へ飛び出すが,A,B,D,E は慣 性の法則によって,
そのまま静止続けよ うとするので飛び出さない。重力がはた らくのでA,B は真下に落ちる。
| 問3 コインはどのような動きをするでしょうか。答えなさい。 | 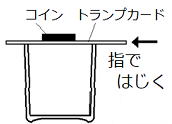 |
|
問1 次の図で,B 君がA 君の背中をおすと どのようになるか。次のア~エから1 つ 選び記号で答えよ。 |
 |
[解答]ウ
[解説] 図のように,A 君はB 君からおされて左向きの力bを受けるので,左方向へ動く。
A 君がB 君をおす力b を作用という。このとき,B 君も,同時に 同じ大きさの逆向きの反作用の力を受 ける。
このことを作用・反作用の法則と いう。反作用の力がはたらくためにB 君は右方向に動く。
なお,(作用) と(反作用)は,「大きさが等しく, 逆向きで,一直線上にはたらいている」 が,
別々の物体(人)にはたらく力であるのでつり合いの関係にはない。
※この単元で特に出題頻度が高いのは 「A,B はそれぞれどちらの方向に動くか」である。
「作用」「反作用」もよく出 題される
■滑車
|
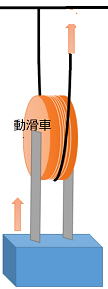
滑車には定滑車と動滑車の2種類があります。 ■動滑車 天井や壁・床などに固定されておらず動くことのできる滑車。 |
  |
定滑車と動滑車について、その違いを以下の問いで考えてみましょう。
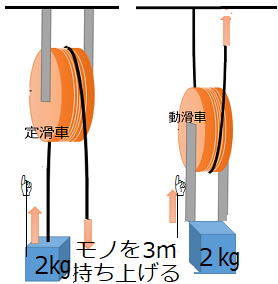
| 🔸定滑車の場合 (1) 糸を何N(ニュートン)の力で引けばよいか。 (2) 糸を何m引けばよいか。 (3) 手がした仕事は何J(ジュール)か。 🔸動滑車の場合 (1) 糸を何N(ニュートン)の力で引けばよいか。 (2) 糸を何m引けばよいか。 (3) 手がした仕事は何J(ジュール)か。 |
 |
解説
100gを1N(ニュートン)としますので、2Kgの物体にはたらく重力は20Nです。
つまり糸を20Nの力で引くと、2㎏の物体を持ち上げることができます。
また糸を何m引くかは、物体を引き上げる長さに等しいはず。よって糸を3m引くわけです。
そして手がした仕事(単位:ジュール)は、以下の公式を使います。
仕事(J) = 力(N)×力の向きに動いた距離 (m) = 20N×3m =60J となります。
(J:仕事の単位 ジュール) m(単位は㍍)で㎝ではありません。
答 定滑車の場合 (1)20N (2)3m (3)60J
動滑車の場合 (1)10N (2)6m (3)60J
定滑車と動滑車について、その違いはなんでしょう?
動滑車を使うと、
・手が引く力は半分。でも手が引く長さは2倍になり、しなければいけない仕事は変わりません。
引く力は半分、引く長さは2倍になり、仕事の量は変わらないことを「仕事の原理」といいます。
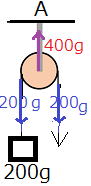
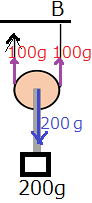
| 問1 (1) 図1で重りを矢印の方向に引っ張って持ち上げるとき、糸を引く力は何gですか。 (2) 図2で重りを矢印の方向に引っ張って持ち上げるとき、糸を引く力は何gですか。 (3) 図1の天井A点には、何gの力がはたらいていますか。 (4) 図2の天井B点には、何gの力がはたらいていますか。 |
図1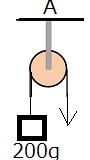 図2 図2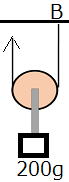 |
| 答えと解説 (1) 200gの重りをつるしているので、「1本の糸にはたらく力の大きさは、どこでも同じ」なので、糸全体に200gの力がはたらくことになります。よって、重りを持ちあげた時に糸を引く力は200gです。 (2) 動滑車に200gの重りをつるしているので、下に引く力の合計は200gです。「下に引く力の合計は、上に引く力の合計と同じになる」ので、上に引く力の合計も200gになります。 上に引く力は左右に2本の糸があるので、左右それぞれ100gの力なら100+100=200となるので、100gの力で引けばOKです。 動滑車の良い点は、このように、重たいものを小さい力で持ちあげることができることです。 (3) 400g (4) 100g |
  |
| 問2 図1、図2の200gの重りに、さらに1kgの重りを加えたときの以下の問いに答えよ。 (1) 図1で重りを矢印の方向に引っ張って持ち上げるとき、(矢 印の方向に)糸を引く力は何Nですか。 (2) 図2で重りを矢印の方向に引っ張って持ち上げるとき、(矢 印の方向に)糸を引く力は何Nですか。 (3) 図1で重りを矢印の方向に2m引っ張るあげるとき、手で ひもを何m引けばいいですか。 (4) 図2で重りを矢印の方向に2m引っ張るあげるとき、手で ひもを何m引けばいいですか。 (5) 図1の天井A点には、何gの力がはたらきますか。 (6) 図2の天井B点には、何gの力がはたらきますか |
|
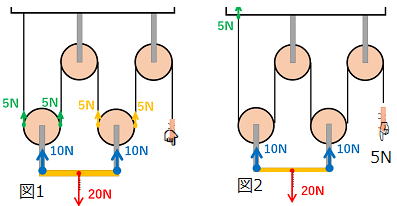
| 問2 右図次のように滑車を組み合わせた装置がある。 これを用いて20Nの重さの物体を3m持ち上げたい。 ただし滑車の重さや糸の重さは考えないものとする。 (1)手で引く力は何Nか。 (2)手で糸を何m引けばよいか。 (3)手でする仕事は何Jか。 |
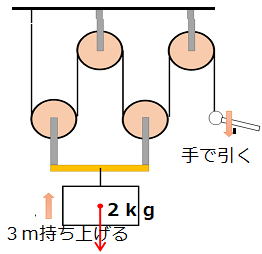 |
(1)・まず動滑車がいくつあるかを数えます。 2kg=20N
・手で引く力は、この場合、動滑車が2個あるので2kgの4分の一、5N …答
(2)・手で糸を引く距離は、動滑車が2個あるので2×2=4倍して、12m …答
(3) 仕事=5N×12m=60J 60Jの仕事をしたことになります。 60J …答
(別解) (1)物体にはたらく重力は20N。 この物体が黄色の棒につるされています。 黄色の棒に20Nの力がはたらいているということです。 この黄色の棒は、2か所で支えられています。 20Nの赤色の力を2か所で支えているのです。 よってこの両端2か所には、それぞれ10Nの力がはたらいていることになります この10Nの力はそれぞれ2つの動滑車によって支えられています。 この10Nの力はさらに糸によって支えられます。 糸の一端は天井に、もう片方の端は手につづいています。 結果的に↓の図のように手と天井が5Nずつ負担していることになります よって手で引く力は5Nとなります (2) 引く力が1/4倍になったのであれば、手で糸を引く距離は4倍になるので12m |
 |
■単元2 生命のつながり
1章 生物の成長とふえ方
図1の写真は一体なんでしょう?
図1 |
図2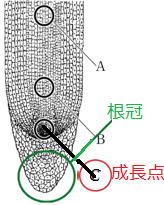 |
実は玉ねぎの根を顕微鏡で写した細胞の写真です。中に細胞の核が見えますね。
それでは図2のA,B,Cのどの部分を写したものでしょう?
答はCです。Cの場所は「成長点」といって、もっとも細胞分裂をくり返し、成長するところです。
図1を見てください。色々なかたちが存在しています。
分裂の初期からすでに細胞分裂しかけているモノなど、生命の神秘といいましょうか。おもしろいですね。
では、どのようにしたら、このような写真が撮れるのでしょう?
以下に、その手順を示します。
⓵まず、タマネギの根を「うすい塩酸」につけ、1分ほど温めます。
うすい塩酸であたためるのは、細胞の1つ1つを離れやすくするためです。
②タマネギの細胞には「酢酸カーミン液」をたらします。
これは細胞の核に色をつけるためです。
③プレパラートに乗せたタマネギを指で押しつぶします。
指で押しつぶすのは、タマネギを平らにし、細胞の重なりをなくして、観察しやすくするためです。
|
図2を見てください。テストにも頻繁に出題されますが、根っこの最も先端と答える生徒さんが多い。 最も先端のこの部分は |
 |
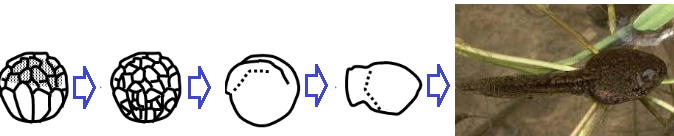
最初、核ひとつだったのが細胞分裂を繰返し、最後は二つになり、細胞が分裂して、
1つの細胞が大きくなることで成長していくのです。
下図はその過程を表しています。

| 上の図はしばしば、どのようにして細胞分裂していくか、 その順番が試験にもよく出題されます。 最初、なんだろうか?と思っていた写真でしたが、 これで右の図が身近に感じてきたかな? |
図1 |
| 問 右図はオオカナダモの葉の細胞を表しています。これを染色液で染め観察したときAの部分がよく 染まった。次の問いに答えなさい。 (1) 染色液でよく染まったAはなんでしょうか。 (2) この実験で使用した染色液はなんでしょうか。 |
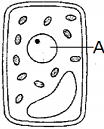 |
答 (1) 核 (2) 酢酸カーミン(酢酸オルセイン)
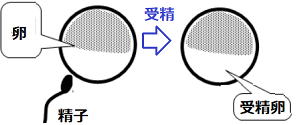
■受精 動物の場合、精子の核と卵の核が合体すること。
植物の場合、精細胞の核と卵細胞の核が合体すること。
■有性生殖 受精によって行われる生殖。
■無性生殖 受精が起こらず行われる生殖。
■生殖細胞 なかまをふやすための細胞のこと。
動物の場合、精子と卵(らん)。
植物の場合、精細胞と卵細胞。
■減数分裂 生殖細胞をつくるための細胞分裂。
(※体細胞をつくるための細胞分裂は体細胞分裂といいます)
生殖細胞にある染色体の本数は、生物のもつ染色体の本数の半分。
例えばヒトのもつ細胞の染色体の本数は46本。
そしてヒトの生殖細胞(精子や卵)の染色体の本数は23本です。
(減数分裂により生殖細胞1つ当たりの染色体数は1/2になるのです)
もし、減数分裂を行わなかったらどうなるでしょう。
| [一問一答] ① 「1個の細胞だけでできている生物を、何といいますか?」 「単細胞生物」 ② 「多数の細胞が集まってできている生物、何といいますか?」 「多細胞生物」 ⑦ 「 |
▲植物の有性生殖
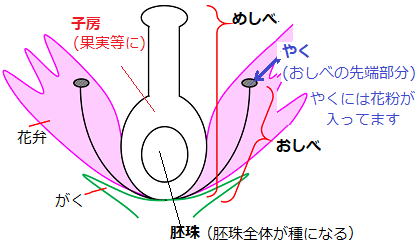
■受粉
| 花粉は風や虫によって運ばれ、めしべの柱頭につきます。これを受粉といいます。 受粉後、花粉からは花粉管と呼ばれる管がのびて、めしべの中を掘り進んでいきます。 この花粉管には精細胞が入っていて |
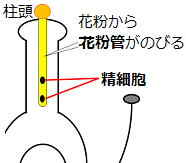 |
| 胚珠の中には卵細胞があります。胚珠まで送り届けられた精細胞は卵細胞と合体します。 このように精細胞の核と卵細胞の核が合体することを受精といいます。 |
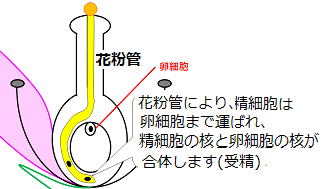 |
| 受精卵はこの後、細胞分裂を繰り返していきます。 そうしたのち ・受精卵→胚 ・胚珠 →種子 ・ |
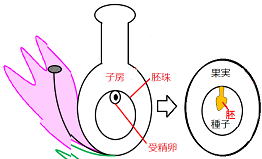 |
▲動物の有性生殖
動物の生殖細胞は精子と
精子がつくられるのはオスのからだにある精巣。
卵がつくられるのはメスのからだにある卵巣です。
この精子の核と卵の核が合体(=受精)して受精卵ができます。
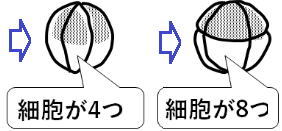
これが“体細胞”分裂を行います。(↓の図)
これにより細胞の数が2つになりました。(体細胞が2つ)
さらに4つ、8つと体細胞の数は増え続けます。
■胚 受精卵が体細胞分裂をしたもの。体細胞分裂をした受精卵のこと。(↓の図)
■遺伝の基本用語
■形質 生物の姿や形、性質のこと。
■遺伝子 形質を決めるもの。染色体に含まれる。
■遺伝 形質が親から子へ伝わること。
■対立形質 対になっている形質。生物には対になっているもののうちどちらかの形質が現れる。
※注 すべての形質が対になっているわけではありません。
対立形質の例
・エンドウの種子の形 →「丸い形」と「しわのある形」
・エンドウの子葉の色 →「黄色」と「緑色」
・エンドウの花の色 →「紫色」と「白色」
・ショウジョウバエの眼の色→「赤色」と「白色」
・ヒトの血液型 →「A型」と「O型」、または「B型」と「O型」
■純系 代々同じ形質ばかり現れる家系のこと。
例えばエンドウの種子の形が親、子、孫・・・と通して同じである場合、これらを純系という。
▲遺伝の規則性
オーストリアの修道士であったメンデルさんはエンドウを使って遺伝の規則性を調べる実験を行いました。
エンドウの染色体にはさまざまな遺伝子が含まれています。その中には
種子の形を「丸」にする遺伝子と種子の形を「しわ有り」にする遺伝子 があります。
いま遺伝子をアルファベットA,やaで表してみましょう。
・種子の形を丸にする遺伝子・・・・・・A
・種子の形をしわ有りにする遺伝子・・・a と表します。
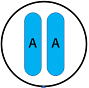
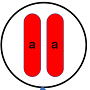
1⃣丸い種子をつくる純系 2⃣しわ有りの種子をつくる純系
種子の形は「丸」なのでこの細胞の中にはAの遺伝子が1つずつ入っています。
しわ有りの種子をつくる純系も同じように染色体が2本で1組となって入っています。
丸い種子をつくる純系のエンドウのめしべ1⃣にしわ有りの種子をつくる純系がつくった花粉2⃣を受粉させて、種子をつくらせてみます。
なかまをふやすため(子孫を残すため)には生殖細胞が必要です。
植物は減数分裂という細胞分裂によって生殖細胞をつくります。
減数分裂では、もとの染色体を別々の生殖細胞に分かれて入ります。
1⃣丸い種子をつくる純系 2⃣しわ有りの種子をつくる純系がそれぞれ減数分裂すると…
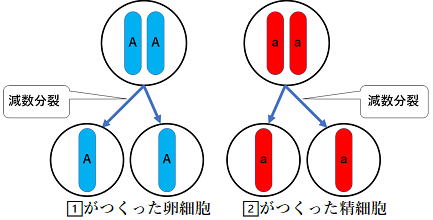 ☜ 受精していない
☜ 受精していない
それでは受精した場合を見てみましょう
減数分裂する際、染色体だけではなく遺伝子も一緒に分かれて生殖細胞に入ります。
・エンドウ1⃣がつくった卵細胞 → 細胞1つにつきAの遺伝子が1つ入っている
・エンドウ2⃣がつくった精細胞 → 細胞1つにつきaの遺伝子が1つ入っている
遺伝子が分かれて入ります。(遺伝子が別々の生殖細胞に入ることを分離の法則といいます)
これらの生殖細胞が受精する(精細胞と卵細胞が合体する)ことを考えてみましょう。
以下のように受精の仕方は4通りあります。
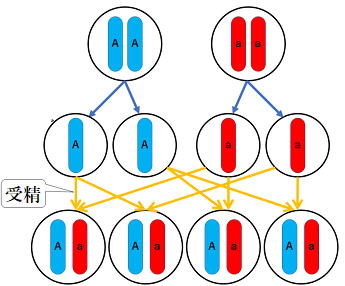
この場合、種子「Aa」で丸い形になります。
「丸としわ」のように対になっている形質はどちらが優先されるかが決まってくるのです。
(影響力の強い遺伝子と影響力の弱い遺伝子があります)
「丸」のように優先される形質(影響力が強い)を
「しわ」のように優先されない形質(影響力が弱い)を
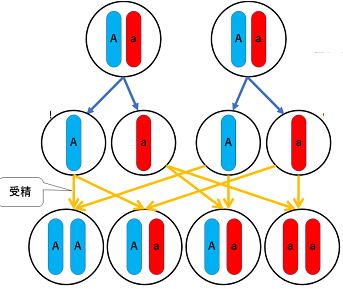
まる まる まる しわ
・Aの遺伝子2つを持った孫(1通り)
・Aの遺伝子1つとaの遺伝子1つを持った孫(2通り)
・aの遺伝子2つを持った孫(1通り) ができます。
・Aの遺伝子2つを持った孫…形質は丸
・Aの遺伝子1つとaの遺伝子1つずつを持った孫…形質は丸
・aの遺伝子2つを持った孫…形質はしわ
まるとしわの数が3:1になりました。
■自然界のつながり
植物はデンプンという有機物をつくっているので生産者といわれます。
動物はその有機物を求めて植物や他の動物を食べるので消費者といわれます。
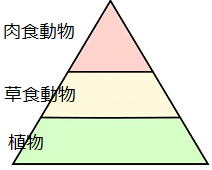
植物…生産者 草食動物/肉食動物…消費者
この食物連鎖のピラミッドは生物の生きる環境によって、
・陸上の生物の食物連鎖
・水中の生物の食物連鎖
・土中の生物の食物連鎖 のように様々な種類がある
■生物どおしのつりあい
①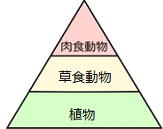 ②
② 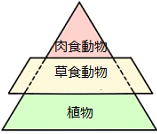
①つり合いがとれた状態 ⇒
②なんらかの環境の変化が起きた結果、草食動物が急激に増えた
③ 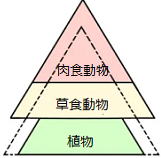
③増えた(増殖)した草食動物に植物は食べられ、植物の数は減少。
草食動物が増え、肉食動物の数も増える
④ 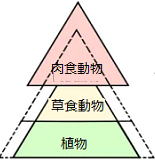 ⑤
⑤
④草食動物が食べる食物が減ったことで、草食動物の数が減少
⑤肉食動物の植物である草食動物が減ったことで肉食動物の数が減少し
元のつり合いがとれた状態に戻る
この生物のつり合いが破れた場合、例えば、
・人間が森林を切り開いて生物の住処を破壊する
・洪水や山火事などで生物の住無場所がなくなる
こうしたことにより、特定の生物が絶滅したり、個体数が急激に減少して元に戻らないといったことがおこる。
分解者のはたらき
分解者・・・生物の死がいや排出物などの有機物を分解して無機物にする生物。
※分解者となるのは菌類、細菌類、土の中の小動物の3種類
菌類・・・カビやキノコのなかま。例:アオカビ、シイタケ、シメジ
細菌類・・・バクテリアとも呼ばれ、肉眼で見えないくらい小さな単細胞生物。
例:大腸菌、乳酸菌、酵母菌
■自然界を循環する物質
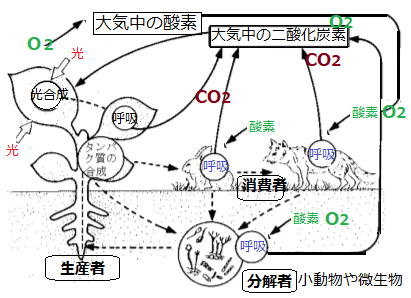
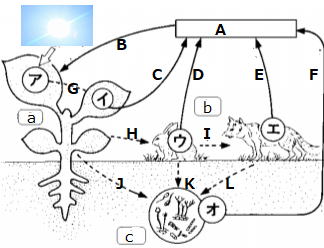
| 問 aの植物や水中のプランクトンは( )者とよばれ、Bで( )Aを取り入れ、 ( )アによって炭素の複雑な化合物であるデンプンなどの有機物をつくります。 bは( )者である。 植物連鎖で有機物の炭素は 植物→( )動物→( )動物と移動する。 この炭素は( )イウエによってふたたび空気中に排出されます。 cは(分解者)で(呼吸)オによって有機物を完全に無機物に変えます。 |
 |
答
aの植物や水中のプランクトンは(生産)者とよばれ、Bで(二酸化炭素)Aを取り入れ、
(光合成)アによって炭素の複雑な化合物であるデンプンなどの有機物をつくります。
bは(消費者)者である。
植物連鎖で有機物の炭素は
植物→(草食)動物→(肉食)動物と移動する。
この炭素は(呼吸)イウエによって、ふたたび空気中に排出されます。
cは(分解者)で(呼吸)オによって有機物を完全に無機物に変えます。
その他
植物は光合成によってデンプンなどの有機物を生産します。
太陽の光エネルギーを使って葉緑体の中で有機物を合成します。
二酸化炭素 +水→有機物+酸素
燃焼は「熱や光を出しながら激しく酸化すること」ですね。有機物は燃やす(化学変化)と
大量の熱エネルギーや光エネルギーを得られることから、化学エネルギーをもっているといえます。
動物は有機物をえさとして食べ、それを消化・吸収して得た養分を細胞内で酸素と反応させ、
生活のエネルギーを得ています。――― 細胞の呼吸
石油・石炭・天然ガスなどは太古の生物(植物プランクトンや植物の破片など)が堆積し、
化石となって変質してできたので化石燃料と呼ばれます。
2学期期末テスト(過去問)
| 1⃣⃣ 右図について答えなさい。 (1) 精子や卵のような子孫を残す特別な細胞を何といいますか。 (2) 受精卵が変化して、生物の体がつくられていく過程を何といいますか。 右図の、受精卵が変化する順を並べ替える問題は必ずといっていいほど出題されます。 |
|
答 (1) 生殖細胞 (2) 発生
| 2⃣ 次の問いに答えなさい。 (1) 右図は被子植物の花の断面を模式的に表している。 a,bの細胞の名を答えなさい。 (2) a,bの細胞がつくられる時に行う特別な分裂を何というか。 (3) 花粉管の先が胚珠にのびて、 aの核とbの核が合体することを何というか。 |
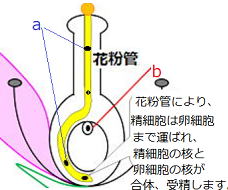 |
|
(4) 次のア~オを有性生殖と無性生殖による増やしかたの2つに分類し、記号で答えなさい。 |
■地球と宇宙

銀河系 (英: the Galaxy)または天の川銀河 (英: Milky Way Galaxy )は太陽系を含む銀河の名称である 。
地球から見えるその帯状の姿は天の川と呼ばれる。
1000億の恒星が含まれる 棒渦巻銀河とされ 、局部銀河群に属している。
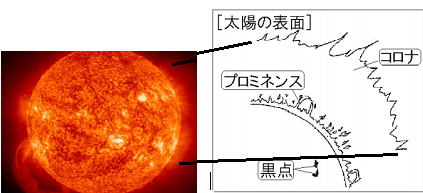
■ 季節の星座の見え方
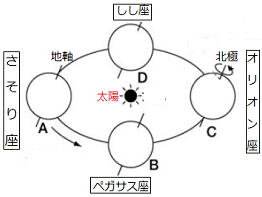
| 右図は、太陽とそのまわりを公転する地球と星座の位置関係を表したものである。これについて、次の問いに答えよ。 (1)地球が太陽のまわりを公転しBの位置にあるとき、日本の季節は何になるか。 (2)地球がBの位置にあるとき、真夜中に南中する星座は何か。右図の中から1つ選び、星座名を書け。 (3)地球がBの位置にあるとき、一晩中観察できない星座はどれか。右図の中から1つ選び、星座名を書け。 (4)地球がCの位置にあるとき、日の出前に南中する星座はどれか。右図の中から1つ選び、星座名を書け。 (5)地球がAの位置にあるとき、真夜中に東の地平線から昇ってくる星座はどれか。右図の中から1つ選び、星座名を書け。 (6)いて座が真夜中に西の地平線付近に見えるのは、地球がA~Dのどの位置にあるときか。1つ選び、記号で答えよ。 (7)地球がAからBに公転するとき、真夜中南中していた星座は、真夜中にどの方角の空に見えるようになるか。 |
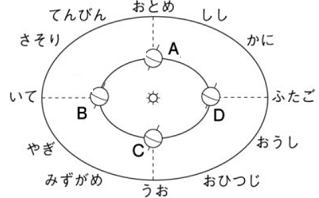 |
(1) 地球の地軸に着目。地球の北極側の地軸が太陽の方向に傾いています。
地球がBの位置にあるときの季節は夏だとわかります。
また、地球がBの位置にあるとき、真夜中に南の空に夏の星座は「いて座」であることが分かります。
夏…答
(2) いて座…答
地球がBの位置にあるとき、真夜中に南の空に見える星座は太陽と反対側にある「いて座」になります。
(3) ふたご座…答
真夜中に観測できない星座は、太陽と同じ方向(太陽の光で見えない)にある「ふたご座」になります。
(4)ふたご座
地球がCの位置にあるとき、日の出前に南中する星座はふたご座になります。
おうし座でないことに注意して下さい。
(5)いて座
地球がAの位置にあるとき、真夜中に東の地平線付近に見える星座はいて座になります。
さそり座ではないことに注しましょう。
(6)C
いて座が真夜中に西の地平線付近に見える地球の位置はCになり、季節は秋になります。
(7)西
地球の公転の影響で、動いていない星や星座は、1か月で30°東から西に動いていくように見えます。
これを年周運動といいました。
■地球の公転と季節の変化
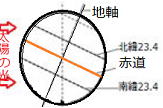
右図は日本が春分、夏至、秋分、冬至の日のときの太陽と地球の位置関係を、模式的に表したものである。
また、下の会話文は、地球の地軸の傾きと公転面との関係についての明くんと舞さんと先生の会話の一部である。
これについて、次の各問いに答えよ。
| 地球は、公転面に垂直な方向に対して、地軸を23.4°傾けたまま公転しています。 地軸の傾きや地球と太陽の位置関係から考えると、日本が春分の日のときの地球の位置は ( ア )です。 もし、地球の地軸が公転面に対していつも垂直であるとしたら、日本付近での太陽の南中高度は、1年を通して南中高度は変化( イ )。 (1) ( ア )にあてはまる記号を、図1のA~Dから1つ選べ。 (2) ( イ )に、下線部のときの日本付近での、1年を通した太陽の 南中高度のようすを、簡潔に書け。 (3) 図2は、地球が図1のCの位置にあるときの、ある時刻の太陽の光と 地球の関係を模式的に表したものである。 この日、地球上のある部分では1日中太陽が出ている。 問題の図の中のその部分をぬりつぶせ。 (4) 図1で、地球がDの位置にあるとき、真夜中、オリオン座は どの方位の空に見えるか。4方位で答えよ。 |
  |
解説
(1) D 北極側の地軸が太陽の方向に傾いているAが夏至の日の地球の位置です。
そこから公転の向きに、Bは秋分、Cが冬至、Dが春分になります。
(2) 南中高度は変化しない
地球の地軸が、公転面に立てた垂線から23.4°傾いたまま、地球の周りを公転していることで、
太陽の南中高度が変化します。したがって、地軸の傾きがない場合、1年を通して南中高度は変化しません。
| (3) 右図で黒く塗りつぶした部分は、地球が自転しても公転面に立てた垂線を超えることはありません。したがって一日中太陽が沈まない白夜になります。逆に北極側の地域は、一日中太陽が地平線から昇らない極夜になります。 (4) 西 Dの位置で真夜中の場合、西の空にオリオン座が見えます。地球を北極側から見下ろした図で考えると分かりやすくなります。 |
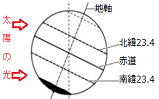 |
問1⃣
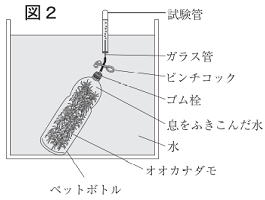
| 明さんは、光合成で使われる物質を調べる実験を行った。以下は,その実験の手順と結果を示したものである。 【手順】オオカナダモを入れた試験管Aと,空の試験管Bを準備する。 次に,水を入れたビーカーに青色のBTB液を加え、 ストローで息を吹き込んで緑色にし,これをA,Bに注いでゴム栓をする。 そして,図1のように,A,Bに十分に光をあてた後,BTB液の色を調べる。 【結果】
|
| 問1 この実験においてBを用いることで.どのようなことを確かめることができたか。 「光」「BTB液」の2つの語句を用いて,その内容を簡潔に書きなさい。 また、この実験でBを用いたように,調べようとすることがら以外の 条件を同じようにして行う実験を何というか。 |
解説 光合成を問う問題です。光のエネルギを使って、ふつう水と二酸化炭素から炭酸水素を合成し、
そのときに酸素を放出します。
・光をあてるだけでは、光合成は行われず、BTB液の色が変化しないこと。
・対照実験
| 問2 【結果】の( )内から,適切な語句を選び,記号で答えよ。 また,この実験の結果からわかる光合成で使われた物質の名称を書け。 |
解説と答
P,二酸化炭素 (答)…青色に変化します。
BTB溶液
| BTB溶液は,水溶液の性質によって色が変わります(右図) アルカリ性…青色 中性…緑色 酸性…黄色 ※ BTB溶液は,アルカリ性に調整され,青色の状態でビンに 保存されています。 [メモ]BTB溶液はそのものがアルカリ性なので青色をしています。実験をする前にBTB溶液に息を吹きかけます。 息の中には二酸化炭素が含まれていて、弱い酸性を示すので黄色に変化します。 そしてオオカナダモが光合成をすると二酸化炭素を使うため、青色に戻ります。 決して酸素がアルカリ性のため青色に変化する訳ではなく、二酸化炭素が使われるため、もとの青色に戻るということになります。 |
 多い ←二酸化炭素→ 少ない |
ここでは問われていませんが、他にリトマス試験紙やフェノールフタレインなどの試験薬を押さえておくことが大切です。
「赤から青に変わった。アルこう」と覚えよう。 また、フェノールフタレインは無色透明から赤色に変化します。
反対にリトマス試験紙が青から赤に変わると酸性。
二酸化炭素が含まれているか否か、石灰水で調べることもあります。白く濁りますね。
問3 実験後,明さんは,下線部に含まれる気体について調べる実験を行うことにした。 |
 |
解答 光合成で発生する気体は酸素です。
答 X:火のついた線香を入れる。 Y:酸素
二酸化炭素は人類が早急に解決しなければならない環境問題です。
世界の科学者が警告を発していますが、消費経済中心の現在、なかなか解決法が見いだせずにいます。
たとえば、アマゾンの森林伐採や私たちも紙の消費を抑えなくてはなりません。
石炭を燃やす火力発電は早急に廃止すべきなのです。
地球誕生以来の氷河や北極や南極の氷も溶け出し、海水面は上昇しています。
海面の温度も上昇し、水害や台風もかつてと違い、その威力を増してきています。
問3⃣
| 水溶液から,溶けている物質をとり出す実験を行った。以下は,その実験の手順を示したものである。 【手順】 ① ビーカーに50℃の水100gを入れ,それに固体の物質Aを40gを加える。 ② よくかき混ぜて,物質Aを完全に溶かす。 ③ ビーカーの中の水溶液を20℃まで冷やす。 ④ ビーカーの中のものをろ過する。 |
| 問1 図1は,手順①で,物質Aを加えた直後のようすを粒子のモデルで表したものである。 手順②で,物質Aが水に完全に溶けたのちのようすを粒子のモデルで表した図として,最も適切なものを,下の1~4から1つ選び,番号で答えなさい。 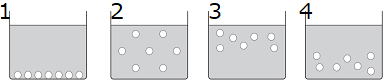 |
 |
答 2
| 問2 下線部「ろ過」の操作を示した図として最も適切なものを,次の1~4から1つえらび、番号で答えよ。 また、この操作によって,ろ紙の上に固体をとり出すことができる理由を,「ろ紙の穴」という語句を用いて,簡潔に書け。  |
答 1 ,固体の物質は、ろ紙の穴より大きいいため、通り抜けることができないから。
| 問3 図2は,物質Aおよび物質Bの溶解度曲線を示したものである。下は,実験後,図2を用いて,水溶液の温度と,出てくる固体の量との関係について考察しているときの,花さんと健さんと先生の会話の一部である。 先生:50℃の水100gに物質A 40gを溶かした水溶液を冷やしていくとき、水溶液の温度が何℃より低くなると固体が出てくると考えられますか。 花さん:(ア)℃より低くなると固体が出てくると思います。固体が出てくるとき,物質Aは溶ける限界の量まで水に溶けているからです。 先生:そうですね。では、水溶液を20℃まで冷やしたとき、出てきた物質Aの固体の量を求めるには,どのように考えればよいですか。 健さん: 50℃で溶かした40gと,20℃で溶ける限界の量である(イ)gとの差で考えることができます。 先生:そのとおりです。 |
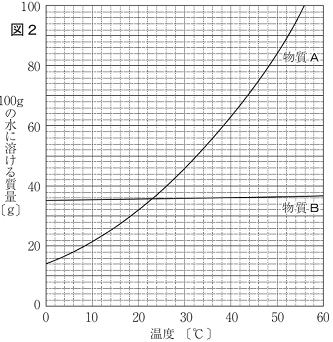 |
| 問 (1) 会話文中の(ア)に入る適切な数値を書け。 (2) 会話文中の(イ)に入る適切な数値を書け。 (3) 50℃の水100gに物質A 40gを溶かした水溶液を20℃まで冷やしていくあいだ、水溶液の濃度はどのように変化すか。「固体が出はじめるまでは,」という書き出しで簡潔に書け。 (4) 図2に示すように、物質Aと比べて物質Bは温度による溶解度の変化が小さい。 そのため、物質Bを溶ける限界の量まで溶かした水溶液を冷やしても,物質Bの固体は少ししか出てこない。 水に溶けている物質Bを,できるだけ多く固体としてとりだすための適切な方法を、簡潔に書け。 |
解説と答 (1) 26℃ (2) 32g
(3) (固体が出はじめるまでは,)濃度は変わらないが、固体が出はじめた後は濃度は小さくなる。
水を蒸発させれば濃度は変わるが、冷やしただけで濃度は変化しない。
(4) 例 水を蒸発させる。
問5⃣⃣
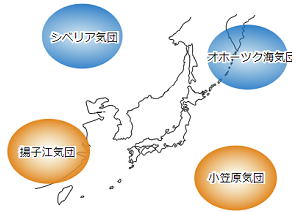
気団の位置と特徴をしっかり把握しておくこと
問6⃣
問7⃣⃣
| 図1のような装置を用いて,電熱線に加える電圧を変えて電流の変化を調べる実験を行った。 図2は,電熱線aとbのそれぞれについて、この実験の結果をグラフに表したものである。 ただし,電熱線以外の抵抗は考えないものとする。 問1 電熱線に加える電圧を変えて電流の変化を調べるための回路を,解答欄の図1の電源装置,電流計,電圧計の全てを導線でつないで完成させよ。 ただし,導線はライン線で表すこと。 |
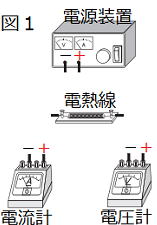  |
答 下図 電圧計は抵抗(電熱線)に並列に接続しますので、最後に接続しましょう。
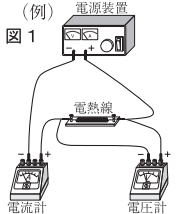 電流計:+に入って−から出る電気の流れに注意
電流計:+に入って−から出る電気の流れに注意
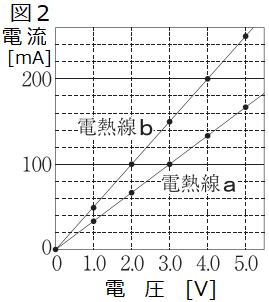
| 問2 下の文章は,図2のグラフから分かったことである。文中の(ア)に下線部のように判断できる根拠となる,図2のグラフの特徴を簡潔に書け。 また、文中の(イ)に入る適切な数値を書け。 電熱線aとbのグラフがともに(ア)であることから,電熱線を流れる電流は電圧に比例する。また、電熱線aとbを比べると,電熱線aの大きさは,電熱線bの抵抗の(イ)倍である。 |
(ア)原点を通る直線 (イ)1.5 a:30Ω b:20Ω
| 問3 次に電熱線aとbを用いて,図3の回路をつくった。電源装置の電圧を6.0Vにして図3の回路に電流を流したときの,回路全体の電力を求めよ。なお、単位も正しく記入すること。 |
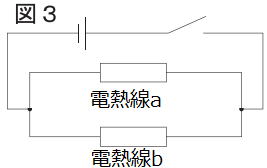 |
電熱線aの抵抗は30Ω bの抵抗は20Ωなので、この場合の全体の12Ω
オームの法則V=IRより電流 I=0.5A
電力W=V・Iから 3.0W
| 問4 家庭内の配線では、さまざまな電気器具が並列につながれている。このように並列につながれているのは,電気器具を使う上で,どのような利点があるからか。その利点を1つ、簡潔に書け。 |
例1:どの電気器具にも同じ電圧がかかる。 一般的に電気器具にかかる電圧は100V
例2:いずれの電気器具の電源オン、オフに左右されない。