| 1節 等差数列と等比数列 1. 数列と一般項 2. 等差数列 3. 等差数列の和 4. 等比数列 5. 等比数列の和 |
2節 いろいろな数列 6. 和の記号Σ 公式 Σの性質 7. 階差数列 8. いろいろな数列の和 |
| 3節 漸化式と数学的帰納法 9. 漸化式 10. 数学的帰納法 |
公式の復習
公式は丸暗記するのではなく、どのようにして導かれたのかという公式の成り立ちを理解し、
その上で暗記することが大切です。
また、数列では、一般化したnの式が求まった後、n=1、n=2など簡単な数字を代入し、
問題と矛盾してないか確認してみましょう。
数列{an}とは
数がある規則に従って横1列に並んでいるものを数列という。
a1 a2 a3 …… an an+1……を、数列{an}で表す。
a1は1番目の数で初項といい、anはn番目の数で第n項といいます。
ポイントは数の並び方の規則性を考えることです。
中学で学習した基本的な問題から学習していきましょう。
| 例 次の数列{an}の第n項anをnの式で表せ。 (1) 2, 4, 6, 8, 10,… (2) 1, 3, 5, 7, 9,… |
(1) 正の偶数でn番目の数は2nです。つまり、an=2n 答
(2) 正の奇数でn番目の数は2n-1です。つまり、an=2n-1
2n+1も奇数になりますが、初項が1だからNGですね。
| 問 次の数列{an}の第n項anをnの式で表せ。 |
答 分母:n番目の数は2n
分子:分子は分母より1大きい数
したがって (2n+1)/2n 答
■等差数列
等差数列{an}の一般項
以下に、公差dの等差数列{an}があります。
a1,a2,a3,a4,……an-1,an,……
公差 +d +d +d +d
n 1 2 3 n−1
a2はどのように表すことができますか?
a2 = a+d のように表すことができますね。以下、
a2 = a1+d, a3 = a1+2d , a4 = a1+3d
これより、第n項の値は以下のようになります。
| |
※一般項は、初項から公差を( n
大切な公式ですので、しっかり理解しておいてください。
※anをnの式で表したものを一般項といいます。
| 例題1 次の等差数列の一般項anを求めなさい。 初項2, 公差6 |
解説)
an=a1+(n−1)でしたね。
代入すると、
an=2+(nー1)×6=6n-4 答
| 問 第4項が14, 第10項が62である等差数列のanの一般項を求めなさい。 |
解説) 初項を a, 公差をd とおくと、
第4項が14 であるから 14=a+(4ー1)d a+3d =14 …①
第10項が62であるので 62=a+(10ー1)d a+9d =62 …②
①,②から a = −10 , d =8 よって、一般項は
an= −10+(n−1)・8 よって一般項は、 an= 8n−18
| 例題2 次の等差数列の第31項を求めなさい。 |
解き方
公差は ![]() ですので、 an=a1+(n−1)d より
ですので、 an=a1+(n−1)d より
a31=3+(31−1)×![]() = -12 (答)
= -12 (答)
それでは問題をやってみましょう。
| 問 (1) 初項3, 公差2の等差数列を第1項から第5項まで書きなさい。
|
答 (1) 3, 5, 7, 9, 11
(2) 3から始まる奇数ですね. an=a+(n-1)d
an=3+2(n-1)=2n+1
(3)an=a1+(n−1)d より
an=9+(n−1)×(-5) =-5n+14(答)
| 例題 等差数列{an}において、a3 =2, a15 = 62であるとき、初項a1と 公差 dを求めなさい。 |
この場合、a1とdをの簡単な連立方程式になります。
an=a1+(n−1)d より
a3 = 2から 2=a1+(3-1)d
2=a1+2d …①
a15 = 62から 62=a1+(15-1)d
62=a1+14d …②
①、②の連立方程式から①-②
-60=-12d d=5(答)
d=5を①式に代入して 2=a1+10 よって、a1 =-8(答)
| 問 等差数列{an}において、a5=30, a 12 =2であるとき、第20項の値を求めなさい。 |
答 an=a1+(n−1)d より
a5 =30なので 30=a1+4d …①
a12 = 2なので 2=a1+11d …②
28=-7d d=-4
②に代入
30=a1-16 a1=46
よって、
a20=46+19×(-4)=-30 a20 =-30 (答)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
・等差数列{an}の和
公差がdの等差数列{an}の、初項から第n項までの和を
Sn = a1+a2+a3,……+an とする。以下の公式が成り立ちます。
重要な公式ですので、しっかり自分のものにしてください。
初項がa1 末項がan、項数がnであるような等差数列の和は
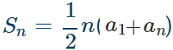 公式② 公式② |
で表せる。 ※ anは末項
末項が分かっている場合で公差は未定です。
大切な公式ですので、しっかり自分のものにしてください。
| 問 初項2,末項が5項で14の場合の、等差数列の和 Sn を求めなさい。 |
公式②に代入 Sn ={(2+14)×5}÷2=40 (答)
| 問 次の自然数の数列の和を求めよ。 |
(1)
![]()
2+4+6+……+98+100
初項
![]()
初項
項数は33-4+1= 30だから
![]() … 答
… 答
考え方:(3)の項数を求め方

さらに、末項が分からない場合の公式を考えてみましょう。
初項2,公差3の等差数列の,初項から第5項までの和Sを求めることを考えてみよう。
S=2+5+8+11+14…① 和の順序を逆にします。
S=14+11+8+5+2…② Sの値は変わりません。 ①+②を計算します。
2S= (2+14)+ (5+11)+ (8+8)+ (11+5)+ (14+2) = 5×16 ( )内の和はすべて16になります。
よって、S= (5×16)/2=40
ここで初項a1,末項を仮にl,項数nの等差数列の公差をdとします。一般に、
初項a1 から第n項 lまでの和を Sn と表すと、次のようになります。
2Sn = n( a1+l ) ![]()
この式に公式① l = a1+(n−1 )d [an=a1+(n−1)d] を代入すると、
以下の公式③が成り立ちます。
| |
初項、公差、項数が与えられたとき(anの値が与えられていない)の初項a1から(第n項)anまでの和
この公式③を覚えなくても公式①と公式②から導きだせますね。
| 問1 (2) (3) |
解答
(1) ![]()
![]()
![]() は 公式① an=a1+(n−1)d から
は 公式① an=a1+(n−1)d から
![]() ={2+(10-1)×3}=29 よって、
={2+(10-1)×3}=29 よって、![]()
|
|
| 1から始まるn個の奇数の和はどのような式になるでしょうか |
1から始まるn個の奇数の和は 1+3+5+7+……+(2n-1)
初項1,末項(2n-1) ,項数nの等差数列の和であるので、
![]() よって 1+3+5+7+……+(2n-1)=n2…答
よって 1+3+5+7+……+(2n-1)=n2…答
基本問題
| (1) 初項が3、公差4の等差数列において、47となる項は第何項か。 (2) 4, k,6kが等差数列であるとき、kの値を求めよ。 (3) 第10項が31、第25項が76である等差数列{an}の一般項を求めなさい。 |
解答
(1) an=a+(n-1)d より
an=3+(n-1)×4=4n-1 4n-1=47 n=12 12項…答
(2) 2k=4+6k より k=-1…答
(3) an=a+(n-1)d より
a+9d =31 …① a+24d =76 …② ①から②を引くと、
d =3, a =4 an=4+(n-1)×3=3n+1 …答
![]()
■等比数列 ![]()
![]()
![]()
![]()
![]()
![]()
等比数列の一般項
隣り合う項の比が等しい数列。この比を公比といい一般的にrで表す。
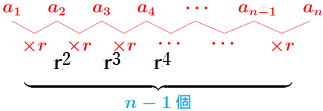
n番目の項anは初項a1に公比r を(n−1) 個 かけた数であるから、
an=a1・r(n−1) …… 公式3 が成り立つ。
例題1 初項が 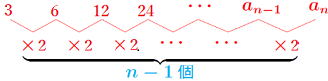 第5項=48, 第6項=96 3 6 12 24 48 96 … an=a1・r(n−1)式に代入すると |
| 例題2 第2項が6、 第4項が24である等比数列{ |
第2項が6、第4項が24だから
初項と公比が分かれば、一般項 an=a1・rn−1 が求められます。
初項を
第2項が6であるから
第4項が24だから arn−1=
②÷①より r=±2
r=2のとき a=3 , r=− 2のとき a =−3
したがって、一般項は
第6項はa6=3・2 6−1 または a6=−3・(−2)6−1
a6=3・25 =94 初項(−3),公比(−2)も同じ94
| 例 次の等比数列の一般項と,第6項を求めなさい。 |
(1) 一般項:
公式が多いようですが、多くの問題を解くことで、自然に慣れていきます。
(2)
よって、一般項:
第6項:
(3)
一般項: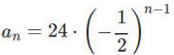 第6項
第6項 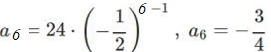
(4)
初項を
②÷①より
一般項:
■等比数列の和
公式4
初項
![]() …公式
…公式
実際にやってみよう
| 例題 初項3,公比2の等比数列の初項から第5項までの和S5は |
公式より 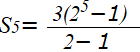 =93
=93
確認してみよう。 3,6,12,24,48 だから 3+6+12+24+48=93
| 問1 初項4,公比3の等比数列の初項から第4項までの和S4は |
公式より ![]() =2×80=160 (答)
=2×80=160 (答)
| 問2 初項8,公比 |
答 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
■いろいろな数列
ここでは主に和の省略記号Σ と階差数列を学びます。
◆和の記号Σ ![]()
和の公式
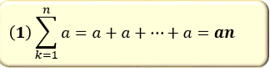
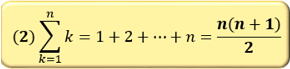
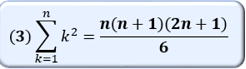 出題率高い
出題率高い
まず等差数列の和をΣで学習しましょう。
例1 数列の和3+3+3+……+n= ![]()
例2 数列の和1+2+3+……+n= ![]()
たとえば1から10まで足すと55になりますね。
公式(2)![]() を使って計算してみましょう。
を使って計算してみましょう。![]()
{10×(10+1)}を2で割ると55
それでは1から100まで足していくといくつになるでしょう。
{100×(100+1)}を2で割ると50×101=5050
ある意味で、このように私たちを楽にするのが数学です。
例3 数列の和12+22+32+……+n2= ![]()
たとえば1+4+9+…を5桁まで足してみましょう。 1+4+9+16+25=55になります。
| 問1 数列の和 2+4+6+……+2n を ①Σを用いて式を書き、 ②解きなさい。 |
① ![]()
・3項までだと単に計算して12 ・n(n+1)に代入すると3×4=12
・4項までだと 2+4+6+8=20 ・式でも4×5=20でOKですね。
このように問題ごとにどの公式を用いるか判断することが大切です。
それでは公式(3)を、実際の数を代入して確かめてみましょう。頻繁に出題される公式です。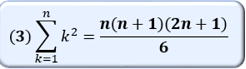 n=3とおいて計算してみましょう。初項1で第3項まで。 |
公式はしっかり押さえておきましょう❕❕
| 問2 数列の和 22+32+42+52+62 をΣを用いて書きなさい。 |
![]() k2 k≠1で表した場合の答です。それでは、以下の問3をやってください。
k2 k≠1で表した場合の答です。それでは、以下の問3をやってください。
| 問3 k=1から始めると、上の式はどのようなΣ式になるでしょうか |
22+32+42+52+62 で
k=1から始めるには、文字式が(k+1)2 となり、項数も5項までになりますね。
![]() (k+1)2 問2の答えは本Σ式でもOKです。
(k+1)2 問2の答えは本Σ式でもOKです。
| 問4 次の和を求めなさい。 ① 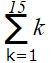 ② ② 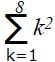 |
① 上の公式(2)より 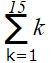 =
=![]() ・15・(15+1)=120(答)
・15・(15+1)=120(答)
② 上の公式(3)より 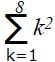 =
= ![]() ・8・(8+1)・(16+1)=204(答)
・8・(8+1)・(16+1)=204(答)
■Σの性質
(1) 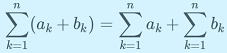 (2)
(2) ![]() c:定数
c:定数
| 例 次の式を具体的な和の式で表し、値を求めよ。 (1) |
解答
(1) (2
与式=1+3+5+7+9+11 (答) 36になります。
(2)
与式=6+9+12+15+18+21 (答) 81
![]() =nである。 右に説明します。
=nである。 右に説明します。 ![]() =
=
| 問1 次の和をΣを用いて表しなさい。 (1) 1+2+3+……+ (2) 1・2 + 2・3 + 3・4 + 4・5 + 5・6 |
(1)1+2+3+……+![]()
(2)1・2 + 2・3 + 3・4 + 4・5 + 5・6 = 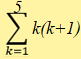
| 問2 次の数列の和を求めなさい。 ① |
①![]() (4k+3)=n(2n+5) ②
(4k+3)=n(2n+5) ② ![]() 3k =
3k =![]() n(n-1)
n(n-1)
④![]() =n でしたね。
=n でしたね。 ![]() ①5=5(n−1)
①5=5(n−1)
問2 次の和を求めなさい。 p23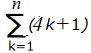 |
Σの性質(1)と(2)から 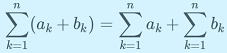
![]() (c:定数)
(c:定数)
公式![]() を使う。
を使う。
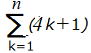 =4
=4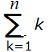 +
+![]() =4×
=4×![]() n(n+1)+n= 2n(n+1)+n
n(n+1)+n= 2n(n+1)+n
=2n(n+1)+n=2n2+3n=n(2n+3) ![]() はn
はn
・なぜ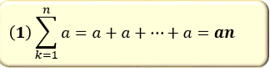 ・では、k=0 のときは |
Σの計算問題
![]()
![]()
![]()
![]()
![]() 作業用
作業用
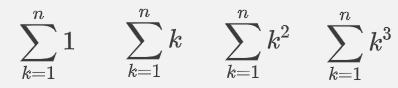
|
練習問題1 例題を参考に、数列式を書いて和を求めなさい ① |
| 練習問題2 次の和を求めなさい ① |
答
① ![]() n(n+1) 一般の公式 ②
n(n+1) 一般の公式 ② ![]() (n-2)(n-1) 一般の公式と違うのはn−2ですね。
(n-2)(n-1) 一般の公式と違うのはn−2ですね。
③ ![]() (k+1)=
(k+1)=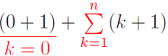 が0から始まっています。k=0を忘れないよう!
が0から始まっています。k=0を忘れないよう!
=1+ ![]() (k+1)= 1+
(k+1)= 1+![]() n(n+1)+n=
n(n+1)+n=![]() {(2+n(n+1)}
{(2+n(n+1)}
=![]() (n+1)(n+2)
(n+1)(n+2)
④ ![]() k=
k=![]() k−
k−![]() k=
k= ![]() n(n+1)−
n(n+1)− ![]() ・3・(3+1)=
・3・(3+1)= ![]() (n−3)(n+4)
(n−3)(n+4)
初項
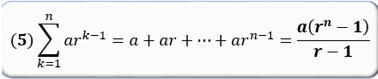
| 「初項3で, 公比r=2 、第4項までの場合で確認してみよう |
そのまま計算すると 3+6+12+24=45
式に代入すると 3(24−1)= 3×15=45 で左辺=右辺
第5項までやってみよう 3+6+12+24+48=93
式に代入すると 3(25−1)= 3×31=93 で左辺=右辺
| 問 「初項4で, 公比r=2 のとき、第6項の値は |
4(26−1)= 4×63=45 252(答)
| 問3 次の和を求めなさい。 (2)計算間違いのないように (1) 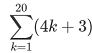 (2) (2)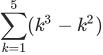 (3) (3)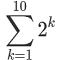 |
(1) 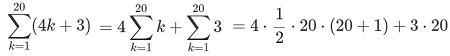 =900
=900
(2) 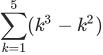
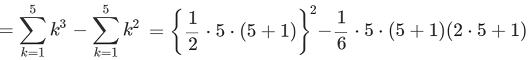 =170
=170
(3) 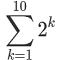 公式 初項
公式 初項
初項2 公比2 2 4 8
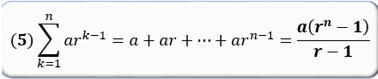 公式 でしたね。
公式 でしたね。
k=1のとき2k=2 だから初項2。公比2,項数10の等比数列の和になります)
2+4+8+16+…+第10項
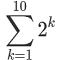
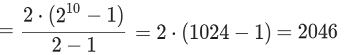
| 数列{ (1) 一般項 (2)初項から第n項までの和を求めよ。 [1997 福岡大] |
{
6 10 14 18
ここで{
![]()
![]()
![]()
![]()
n=1のとき 2n2+3=5 初項は5であるのでn=1のときも上式は成り立つ。
したがって
| 問 次の和を求めなさい。p22 ① 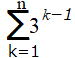 ② ②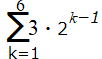 |
① 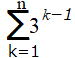
![]() 3の0乗は1だから、初項1。 公比=3,n項
3の0乗は1だから、初項1。 公比=3,n項
② 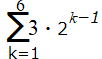 =
= ![]() = 63 初項3,公比2,6項
= 63 初項3,公比2,6項
p24から
下の5つの公式はしっかり押さえておこう!
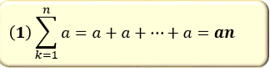
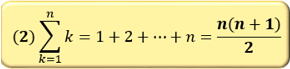
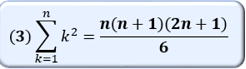
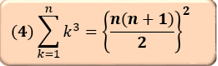
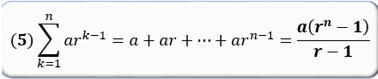
初項a 公比rの等比数列の総和の公式
(3),(4)の公式は直感的な理解が難しく、丸暗記したほうが早いです。
|
問 次の和を求めよ |
解答
(1) ![]() (2k+1) = 2
(2k+1) = 2![]() k +
k + ![]() 1 = 2×
1 = 2×![]() n(n+1)+n= n(n+2)
n(n+1)+n= n(n+2)
(2)![]() (6k2−4k−5)= 6
(6k2−4k−5)= 6![]() k2−4
k2−4![]() k −
k −![]() 5
5
=6×![]() n(n+1)(2n+1)−4×
n(n+1)(2n+1)−4×![]() n(n+1)−5n= n(n+1)(2n+1)−2(n+1)−5n
n(n+1)−5n= n(n+1)(2n+1)−2(n+1)−5n
= n(2n2+n−6)= n(n+2)(2n−3) …答
|
問 次の式が 32+52+72+92+112+132 を表すように |
まず、数の並び方の規則性を考えることです。
すべて2乗で、3, 5, 7, 9, 11, 13に着目します。
奇数なので2
初項は3ですので、(2
![]()
■階差数列と数列の和
階差数列とは 数列{an}の隣り合う2つの項の差 bn=an+1−an
を項とする数列{bn}を、数列{an}の階差数列といいます。
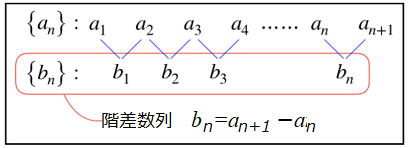
例えば {an}: 1, 2, 5, 10, 17, 26, 37…の階差数列は以下
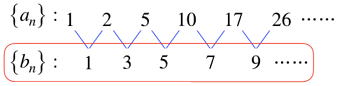
となり、{bn}は初項1、公差2の等差数列になります。
| 例題1 階差数列を考えて、1, 3, 7, 13,21 ……の第6項を求めてみよう。p87 |
{an}: 1, 3, 7, 13, 21…
{bn}: 2 4 6 8
bn=2n よって、数列{an}の第6項は (階差数列式 bn=an+1−an)より
a6−a5=b5 a6=a5+b5=21+2×5=31 (bn=2n から b5=10)
p88
数列{an}の階差数列を{bn}とすると、
n≧2のとき、 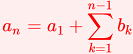
この式はn≧2のとき、制限付きなので注意しましょう。
n=1のときΣ記号がk=1から0までの和となってしまい、
数列の和 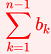 のΣによる計算ができないからです。
のΣによる計算ができないからです。
n=1のときは、求めた一般項にn=1を代入し、必ず確認しましょう。
数列{an}の隣り合う2つの項の差bn=an+1−an (n=1,2,3,…)を項とする数列{bn} を、
数列{an}の階差数列といいます。
また数列{an}の階差数列を{bn} とすると、
n≧2のとき一般項は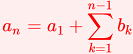 でしたね。それでは実際にやってみよう。
でしたね。それでは実際にやってみよう。
| それでは、まえの例題1を階差数列の一般項から求めてみよう。 1, 3, 7, 13,21 ……の第6項を求める問題でしたね。 |
an=1, 3, 7, 13, 21,…
bn= 2 4 6 8 となり、これは初項2,公差2の等差数列ですね。
bn=2n したがって、
n≧2のとき an=a1+![]() bk=1+
bk=1+![]() 2k
2k
=1+2![]() k= 1+2・
k= 1+2・![]() (n−1)n
(n−1)n
=n2−n+1 左式に n=1 を代入すると初項=1で左式は成り立ちます。
36−6+1=31 31になりますね。
ちなみに第7項を求めてみよう。
an=1, 3, 7, 13, 21, 31, □…
bn= 2 4 6 8 10 12 で□内は43になりますね。
上のn2−n+1に代入すると、第7項なので 49−7+1=43でOKですね。
第7項までは普通の計算で解けますが第50項や7,80項となるとそうはいきませんね。
| 例題 次の数列{an}の一般項を求めよ。🄿27 4, 7, 12, 19, 28, 39 ……n |
数列{an}の階差数列を{bn}とすると、{bn}は
{an} = 4, 7, 12, 19, 28, 39 …
{bn} 3 5 7 9…
となる。これは初項3,公差2の等差数列であるから、
bn=3+(n−1)2=2n+1
したがって, n≧2のとき
an=a1+![]() bk=4+
bk=4+ ![]() (2k+1)=4+2
(2k+1)=4+2![]() k+
k+![]() 1
1
=4+2![]() k+
k+![]() 1=4+2・
1=4+2・![]() (n−1)n+(n−1)
(n−1)n+(n−1)
=n2+3 a1=4 であるから本式はn=1のときも成り立つ
よって an=n2+3
| 数列 2, 3, 5, 8, 12 … の一般項を求めてみよう。 |
2, 3, 5, 8, 12 … は
1 2 3 4 初項1 公差1
{an}=2, 3, 5, 8, 12 …とすると、
階差数列{bn}=1,2,3,4…となる。
よって{bn}=n 1+(n−1)×1
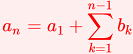
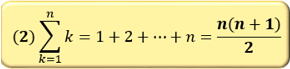
n≧2のときan=2+![]() k
k
n−1までなのでn → n−1
an=2+![]() n(n−1)=
n(n−1)=![]() n2−
n2−![]() n +2 =
n +2 = ![]() (n2−n+4) …①
(n2−n+4) …①
①式はn=1を代入すると2になり①式を満たす。
![]()
■漸化式
次の2つ(1),(2)が与えられると数列を定めることができる。
(1) 初項
(2) 前の項からその次に続く項を定める規則
例えば an+1= an+3 仮に初項を1とすると a1 = 1[n=0]
a2 = a1+3 = 1+3= 4 [n=1]
a3 = a2+3=4+3=7[n=2]
a4 = a3 +3=10 [n=3]
an+1= an+ 3 のように(2)の規則を表した式を漸化式といいます。
| 例題1 次の条件で定められる数列のa2,a5を求めなさい。(n=1,2,3,4…) ① a1=3 , an+1= 2an-1 ② a1=1 , an+1= an+n |
解説 ① 式から、等差数列であることが分かる。初項は3
a2= 2a1-1=2×3-1=5 [n=1]
(同様に a3=2a2-1= 9 [n=2],a4=2a3-1=17 [n=3])
a5= 2a4-1=33 a2=5,a5=33
② a2=のとき a2= a1+n = 1+1= 2 [n =1] よってa2=2(答)
(同様に a3= a2+n=4 [n =2] a4= a3+n a4=7 [n=3]
a5= a4 +n [n=4] a5=11
| 問1 次の条件で定められる数列のa2,a5を求めなさい。(n=1,2,3,4…) a1=2 , an+1= 2an-3 |
a2= 2a1-3= 2×2-3=1 [n=1]
2、1、−1、−5,−13
−1 −2 −4 −8 で変化
(同様に a3 = 2a2-3=-1,a4=2a3-3=-2-3=-5
a5= 2a4-3=-13
■漸化式と一般項
漸化式の3つの基本パターン
・等差数列型の漸化式 an+1-an= d (d:公差) …①
・等比数列型の漸化式 an+1=ran (r:公比) …②
・階差数列型の漸化式 an+1=an+bn (bn:階差数列の一般項)…③
(教科書によってはf(n)とおく場合もある)
① まずは等差数列型の公式①を用いて公差を求めましょう。
an+1=an+4
この式を、等差数列型の式の形に変形します。
an+1−an=4 等差数列型の式
| 初項が3、公差が4の等差数列の一般項は |
an=3+(n−1)4 よって an=4n−1 となります。
② 次に初項が2の等比数列型の公式②を用いて公比を求めましょう。
an+1 + 3an =0
この式を、等比数列型の式の形に変形しましょう。
an+1 =− 3an
これにより初項が2公比が−3の等比数列なので一般項は
an =2・(− 3)n−1 となります。
③ 最後に階差数列の漸化式をみていきましょう。階差数列の一般項の公式を思いだしましょう。
階差数列の一般項は an =a1+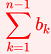 でしたね。
でしたね。
漸化式では初項と公比を求めることができ、それを用いて等比数列の一般項の公式を解き、
一般項を求めることができます。実際にやってみましょう。
階差数列型の漸化式 an+1=an+bn (bn:階差数列の一般項)
| 例題1 次の条件で定められる数列{an}の一般項を求めてみよう。 a1 =1 , an+1 =an+4n |
① a1 =1, an+1 =an+4n 移行 a1 =1, an+1−an=4n
数列{an}の階差数列の第n項が4n なので、4 8 12 16
n≧2のとき、公式から an =1+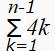
=1+4・![]() n(n−1) 公式参考
n(n−1) 公式参考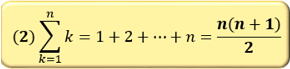
=2n2−2n+1 これは n=1のときも満たす。よって、
an =2n2−2n+1
| 例題2 次の条件で定められる数列{an}の一般項を求めてみよう。 a1 =2, an+1 =an+3n n≧2のとき、公式から an =2+ |
| 例題 a1 =5 , an+1 =4an− 6 (n=1,2,3,4…)によって定められる数列{an}の一般項を求めてみよう。 |
an+1 =4an− 6 の漸化式を変形します。 an+1 −2=4an− 6−2
an+1−2 =4(an− 2)
次にbn=an− 2 とすると、(an+1−2)=bn+1 bn+1 =4bn
これより数列{bn}は公比4の等比数列であることが分かります。
数列{bn}の初項は b1 =a1−2 = 5−2 = 3
数列{bn}の一般項は bn= 3・4n−1 したがって数列{an}の一般項はan=bn+ 2
an=3・4n−1+2 となります。
練習問題
| 問1 次の条件で定められる数列の{an}の一般項を求めなさい。 (n=1,2,3,4…) ① a1=2 , an+1 = an-3 ② a1=4 , an+1=-3an 初項2 公差d ー3 初項4 公比r ー3 |
解説
① a1=2 , an+1 = an-3 (n=1, 2, 3, 4…) で定められた数列は、
初項2、公差-3の等差数列であるから
公式① ![]() を思いだして、
を思いだして、
an =2+ (n-1)・(-3) =-3n +5 答
| |
② a1=4 , an+1=-3an (n=1,2,3,4…) で定められた数列は、
初項4、公比-3の等比数列であるから
| an=a1・r(n−1) 公式② |
an =4・(-3)n-1 … (答)
| 問2 次の条件で定められる数列の{an}の一般項を求めなさい。 ① a1=2 , an+1 = an + 3 ② a1=1 , an+1= -30n ③ a1=3 , an+1-an =-5 ④ a1=-5 , an+1-20n=0 |
解説
① a1=2 , an+1 = an + 3は等差数列
an =2+3(n-1)=3n-1
② a1=1 , an+1= -30nは等比数列
an=a1・r(n−1) より an = (-30)n-1 (答)
③ a1=3 , an+1 -an =-5 (an+1=an-5)
an = 3+(-5)(n-1)= -5n+8
④ a1=-5 , an+1-20n=0 (an+1=20n)
an=-5・2 n-1
| 問 ① 初項をa、公差をdとしたとき、この数列の一般項anは an= ② 初項がa、公差をdである等差数列において、初項から第n項anまでの和Snは Sn= ③ 初項がa、公比をrとしたとき、この数列の一般項anは an= ④ 初項がa、公比をrである等比数列において、初項から第n項anまでの和Snは 公式 ⑤ 公式 ⑥ 公式 ⑦ ⑧ 数列{an}の隣り合う2項の差を項とする階差数列{bn}は bn= ⑨ 数列{an}の階差数列を{bn}とすると n |
① 初項をa、公差をdとしたとき、この数列の一般項anは
an=a+(n−1)d
② 初項がa、公差をdである等差数列において、初項から第n項anまでの和Snは
Sn=![]() n(a+an) an:末項
n(a+an) an:末項
③ 初項をa、公比をrとしたとき、この数列の一般項anは
an=a・rn−1
④ 初項がa、公比をrである等比数列において、初項から第n項anまでの和Snは
![]() …公式
…公式
公式
⑤ ![]() aのとき
aのとき ![]() +
+![]() +
+![]() +……
+……![]() =
= ![]() n a:定数
n a:定数
公式
⑥ ![]() kのとき
kのとき ![]() +
+![]() +
+![]() +……
+……![]() =
=![]()
公式
⑦ ![]() k2のとき
k2のとき ![]() +
+![]() +
+![]() +……
+……![]() =
=![]()
⑤~⑦までは 以下を参照
⑤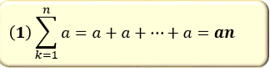 ⑥
⑥ 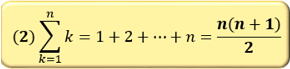
⑦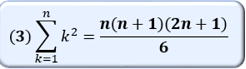
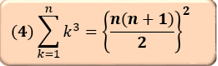
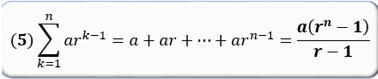
初項a 公比rの等比数列の総和の公式
⑧ 数列{an}の隣り合う2項の差を項とする階差数列{bn}は bn = an+1−an
⑨ 数列{an}の階差数列を{bn}とするとn≧2のとき (初項:a1)
n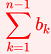 (階差数列の一般項)
(階差数列の一般項)
3/2 n=1
| 問 次の数列{an}の一般項を求めよ。また、初項から第 (1) 1・3, 2・4,3・5,4・6, … (2) 3・5, 5・7,7・9,9・11, … |
(1) 1・3, 2・4,3・5,4・6, …
一般項はn(n+2) Sn=![]() k(k+2)=
k(k+2)=![]() k2+
k2+![]() 2k
2k
=![]() n(n+1)(2n+1) +2・
n(n+1)(2n+1) +2・![]() n(n+1)=
n(n+1)=![]() n(n+1){(2n+1)+6}
n(n+1){(2n+1)+6}
=![]() n(n+1)(2n+7) …答
n(n+1)(2n+7) …答
(2) 3・5, 5・7,7・9,9・11, …
一般項は(2n+1) (2n+3) Sn=![]() (2k+1)(2k+3)=4
(2k+1)(2k+3)=4![]() k2+8
k2+8![]() k+
k+![]() 3
3
=![]() ・4n(n+1)(2n+1) +8・
・4n(n+1)(2n+1) +8・![]() n(n+1)+3n=………
n(n+1)+3n=………
| 問 次のように定められた数列{an}の一般項を求めなさい。 p32 a1=3 , an+1 = an + 2n (n=1,2,3,4…) |
an+1−an = 2n であるから、数列{an }の階差数列の一般項は2nである。
したがって、n≧2のとき、
an = a1 +![]() 2k=3+2
2k=3+2![]() k=3+2・
k=3+2・![]() n(n−1)=3+n(n−1)
n(n−1)=3+n(n−1)
(2)の公式n(n+1)はn(n−1)になりますね。
| 問 a1=1, an+1= an+2n−2n (n=1,2,3,4…)で定義される数列の一般項anを求めよ。(法政大入試) |
条件より an+1− an=2n−2n
数列anの階差数列の第n項が2n−2n であるから
n≧2のとき
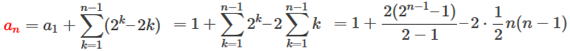
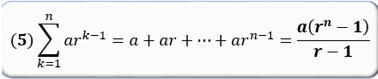 を使う。
を使う。
![]()
初項はa1=1なので 結果はn=1 のときも成り立つ。
したがって ![]() (答)
(答)
| ChallengeΣ 二項定理で(a+b)nを展開したとき,
Σで以下のように表せます |
■ 数学的帰納法
数学的帰納法は「自然数nに関する命題が、すべての自然数について成り立つ」ということを証明することで、
①n= 1 のときに命題が成り立つことを証明する。
②n= kで命題が成り立つと仮定すると、n=k+1でも命題が成り立つことを証明する
この2つの手順を踏んで証明することです。
この①②が証明できれば、
「①よりn= 1のとき命題は正しくて、②よりn= 1のときに命題が正しいのだからn= 2のときも命題は正しくて、
そうするとまた②よりn= 2のときに命題が正しいからn= 3のときも命題は正しくて…」
というのを無限に繰り返せるので、すべての自然数について命題が正しいことになります。
①で証明するのがn= 1,2になったり、②で証明するのがn= k+2だったりと、
扱う文字や項は問題によって変わってくるものの、
「一番小さい数たちを入れたときに命題が成り立つこと(①)」と「つながりが成立すること(②)」を証明することで、
どのようなnでも命題が成り立つことが証明できるのです。
実際にやってみましょう。
| 【例題】nが自然数のとき、 公式 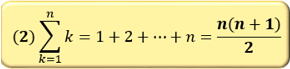 1+2+3+…+ n-1 +n= |
【解説】1+2+3+……+ n-1 +n = ![]() を証明します。
を証明します。
数学的帰納法の手順は、以下の通りでした。
① n=1のときに命題が成り立つことを証明する
② n=kで命題が成り立つと仮定すると、n=k+1でも命題が成り立つことを証明する
でした。これに沿って考えていきましょう。
まず、n=1のときに公式(2)が成り立つことを証明します。
n=1のとき、左辺 1+2+3+…+n-1+n =1
右辺は ![]() n=1 右辺も1になる。
n=1 右辺も1になる。
よって、n=1のとき正しいことが示せた。
次に、n=kで命題が成り立つと仮定し、n=k+1でも命題が成り立つことを証明します
n=k (kは自然数)のとき命題が成立すると仮定すると、
1+2+3+…+(k−1)+ k = ![]() …① 仮定
…① 仮定
このとき、n=k+1 を考えると
①の左辺 = 1+2+3+…+k+(k+1)=![]() + k+1 ※(k+1)を前にくくり出そう。
+ k+1 ※(k+1)を前にくくり出そう。
右辺 =![]() (k+1)(k+2) =①の右辺
(k+1)(k+2) =①の右辺
よって、n=kを仮定すると、n=k+1でも命題が成立することが示せた。
すべての自然数nについて命題が成り立つ
| 問 2以上の自然数nにおいて |
解答
(1) n=2のとき![]() の左辺=22= 4 右辺=2×2=4
の左辺=22= 4 右辺=2×2=4
左辺=右辺で式は成りたつ。
(2) n=k (kは2以上の自然数)のとき、与えられた式が成立すると仮定すると、
2k≧2k …①
このときn=k+1 を考えると
与えられた式![]() の左辺=2k+1 = 2k×2
の左辺=2k+1 = 2k×2
右辺=2(k+1)=2×2k で 2k+1 ≧2(k+1)
よってn=kを仮定するとn=k+1
![]() が成り立つことが示せた。このことからすべての自然数nについて
が成り立つことが示せた。このことからすべての自然数nについて![]() が成り立つ。
が成り立つ。
再度、確認しましょう
一番基本的な数学的帰納法は、
「自然数nに関する命題Pが、すべての自然数について成り立つ」ということを
①n=1のときに命題Pが成り立つことを証明する
②n=kで命題Pが成り立つと仮定すると、n=k+1でも命題Pが成り立つことを証明する
この2つの手順を踏んで証明することです。