1節 整式・分数式の計算 戻る
目 次
| 1章 式と証明 復習 1.複素数 2.2次方程式 1節 式と計算 1 3次の乗法公式と因数分解 2 二項定理 3 整式の割り算 4 分数式とその計算 5.等式/不等式の証明 (相加/相乗平均) 乗法公式や因数分解の苦手な人はここをクリック してください。 |
3.高次方程式 剰余の定理と因数定理
さらに、x2−2x+5=0 すなわち(x−1)2= −4 のような2次方程式では
x−1=±![]() √−4
√−4
x−1=±2i x= 1±2i になります。
| 次の式を計算しなさい。 ① |
![]()
| 問1 以下の計算をやってみよう。 ①2i+3i= ②2i−3i= ③−2i−3i= ④2i×3i= ⑤2i÷3i= ⑥ |
答 ① 5i ② −i ③ -5i ④ -6 ⑤ 2/3
⑥ ![]()
| 問2 次の計算式を簡単にしなさい。 |
答 (1) ![]() (2)
(2)![]() (3)
(3)![]() (4)
(4) ![]()
(5)![]() ※ 以下、
※ 以下、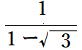 の有理化と同じ考え方で解けますよ。
の有理化と同じ考え方で解けますよ。
(6)![]() (7)
(7)![]() (8)
(8)![]()
![]() (判別式)
(判別式)
高校2年で二項定理を学習します。
そのまえに、以下の因数分解を理解しておく必要があります。
数学の基礎中の基礎で、非常に大切です。マスターしましょう。
中3で習った乗法公式です。非常に大切な公式なので、忘れた人は思い出そう。
2次の乗法公式(復習)
展開 ⇆ 因数分解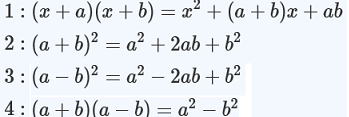 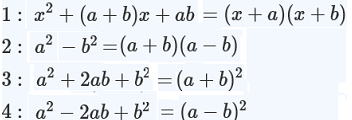 |
復習問題1 次の2次方程式を因数分解し、 |
答
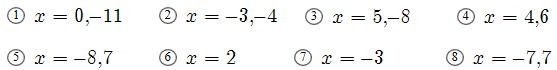
多少難しくなりますが、続けて以下の2次方程式を解いてください。
復習問題2
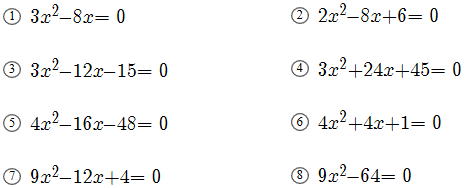 |
答
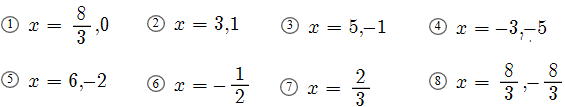
![]()
![]()
| 上の式は中学で学習した公式です。思いだして、(1)から(2)まで やってみましょう。 (1) (3) |
答 (1)![]() (2)
(2) ![]()
(3) ![]() √の中がマイナスになりますね。虚数です。
√の中がマイナスになりますね。虚数です。
判別式と解の種類
解はどのようなものか、実数解が±の2つなのか、
√の中が0でしたら±以降が0ですので、実数解が1つになり、
√の中がーでしたら虚数解になりますね。
つまり√、根号の中の式の値により解の種類が判別できます。
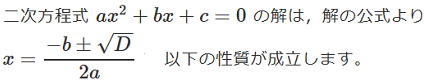

| 問1 次の2次方程式の解を判別しなさい。 問2  |
答
問1(1) D=17より異なる2つの実数解をもつ
(2) D=12 より異なる2つの実数解をもつ
(3) D=-11 より異なる2つの虚数解をもつ
(4) D=0より重解をもつ
問2

![]()
![]() の解は
の解は ![]()
この2つの解の和と積の関係はどのようになるでしょう。
![]()
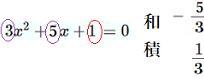 一般に次の式が成り立ちます。
一般に次の式が成り立ちます。
公式
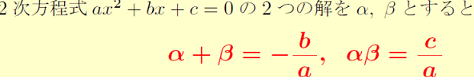
例 ![]() の2つの解をα、βとするとき、
の2つの解をα、βとするとき、
αとβの和と積は次のようになります。
和はα+β=![]() 積はαβ=
積はαβ=![]()
| 問1 2次方程式 次の値を求めなさい。 (1) α2β+αβ2 (2) |
答 (1) 30 (2) 6/5
| 問2 2次方程式 次の値を求めなさい。 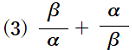  (5) α2β+αβ2 |
解答 α+β=2 αβ=![]() より
より
![]() = αβ+2(α+β)+4
= αβ+2(α+β)+4
![]() …答
…答
(2) ![]() = (α+β)2ー2αβ=4-3=1 …答
= (α+β)2ー2αβ=4-3=1 …答
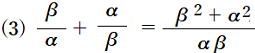
![]() …答
…答
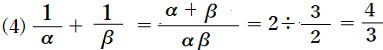 …答
…答
(5) α2β+αβ2=αβ(α+β)=3 …答
| 問3 2つの数2+√5 , 2-√5を解とする2次方程式を1つ求めなさい。 |
解答
和 (2+√5)+(2ー√5)=4
積 (2+√5)(2ー√5)=4-5=-1 だから、
![]()
| 問4 2次方程式 α+2,β+2を解とする2次方程式を1つ求めなさい。 |
| 例 |
まず、 ![]() とおきましょう。
とおきましょう。
![]() ですので、(
ですので、(![]() -2)が因数になります。よって、
-2)が因数になります。よって、
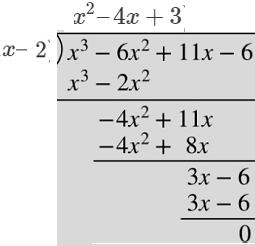 (
(![]() -2)(
-2)(![]() -3)(
-3)(![]() -1) …答
-1) …答
今回、P(2)から始めましたが、P(1)=0から始めたほうが楽ですね。
| 問 因数分解しなさい |
![]() とおく
とおく
![]() ,
,![]() ではP(
ではP(![]() )=0にならないね。
)=0にならないね。
![]() ですので、(
ですので、(![]() -2)が因数になりますね。
-2)が因数になりますね。
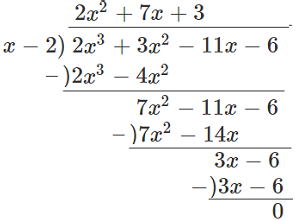
![]()
![]() …答
…答
3つの因数に分解できました。
| 例1 以下の方程式を解いてみよう |
ヒント ![]() に1を代入、NGならー1…。解決する糸口が見えてきます。
に1を代入、NGならー1…。解決する糸口が見えてきます。
![]() =-1, 2±2√2…答
=-1, 2±2√2…答
1節 式と計算
1 3次の乗法公式と因数分解
| 展開の公式
|
公式を確認してみよう
![]() を
を
![]() のようにして展開し、確かめてください。
のようにして展開し、確かめてください。
同様に以下の公式をも確かめてください。
![]()
![]()
![]()
上の式の反対、因数分解はよく使いますので、ここで形として覚えてしまいましょう.。
問題を数多く解答することで、公式になれることが大切です。
それでは下の公式を展開、または因数分解してみましょう。
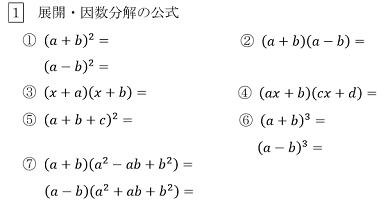 |
解答
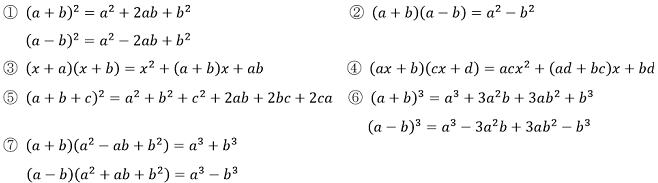
2 二項定理
二項定理は![]() や
や![]() のような2項の累乗の式、つまり
のような2項の累乗の式、つまり
![]() を展開をするときに大変便利です。(各項の係数を求めるとき)
を展開をするときに大変便利です。(各項の係数を求めるとき)
係数で考えてみましょう。
![]() の係数は1a、1bで係数は 1 と 1 (上のパスカルの3角形でn=1のとき)
の係数は1a、1bで係数は 1 と 1 (上のパスカルの3角形でn=1のとき)
![]() の係数は
の係数は
![]() ですから 1 2 1 (n=2のとき)
ですから 1 2 1 (n=2のとき)
![]()
![]() 係数は1 3 3 1 (n=3のとき)
係数は1 3 3 1 (n=3のとき)
係数の変化にある一定の法則が考えられますね。
n乗で考えてみましょう。以下のようになります。
![]() において、係数だけを左から (aの次数の高い順に)
において、係数だけを左から (aの次数の高い順に)
■ パスカルの三角形
| n=0のとき n=1 〃 n=2 〃 n=3 〃 n=4 〃 |
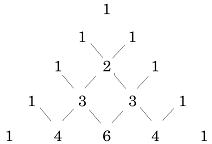 |
つまりパスカルの3角形から以下の形になります。

ただ、パスカルの3角形は書くのに大変?
そこで、以下のやり方をお勧めします。
1 1
1 1
1 2 1 2乗
1 2 1
1 3 3 1 3乗
1 3 3 1
1 4 6 4 1 4乗
といった具合に右へ1つずつ移動させるとやり易いですね。
| ・ = ------------------------------------------------------------- ・ = = -------------------------------------------------------------- ・ = = |
この方法で5、6乗まで解決しますが、10,20乗となれば大変ですね。
nCrという立派な式がありますが、これはあと(二項定理)で触れたいと思います。
では、![]() を展開してみましょう。5乗の展開なので
を展開してみましょう。5乗の展開なので
パスカルの三角形から係数は 1 ,5, 10, 10, 5, 1
以下のようになります。
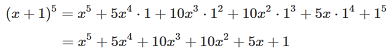
| それでは以下の問題(展開)にチャレンジしてみてください。 ① ③ |
① (![]() +2)3=
+2)3=![]() +(3
+(3![]() ) ×2 +(3
) ×2 +(3![]() )×(2)2+(2)3
)×(2)2+(2)3
=![]() +6
+6![]() +12
+12![]() +8
+8
②
③ (![]() -2)3=
-2)3=![]() -(3
-(3![]() ) ×2 +(3
) ×2 +(3![]() )×(2)2-(2)3
)×(2)2-(2)3
=![]() -6
-6![]() +12
+12![]() -8
-8
| 問1 (1), (2) 因数分解、(3)~(6) は展開しなさい (1) (3) (5) (3x+2)3 (6) (x-2y)3 |
答 公式に慣れることです。そのためには、数多くの問題を解くことです。
(1)![]()
(2) ![]()
「3乗の式ですから、まず、64は4の3乗では?」と考えることです。
(3) ![]()
計算ミスに注意
(4)![]()
(5) (3x+2)3= (3x)3+3×(3x)2×2+3×(3x)×22×23
= 27x3+54x2+36x+8
(6) (x-2y)3 = x3+3×x2×(-2y)+3×x×(-2y)2×(-2y)3
= x3-6x2y+12xy2-8y3
| チャレンジ 前例のパスカルの三角形(図2)はncrを用いて図3のように置き換えられます。
図2 図3
以下のようにも表せます |
1章で学んだ以下の公式。大切ですので左辺から右辺へ(展開)、右辺から左辺へ(因数分解)
スムーズにできるようにしておいてください。
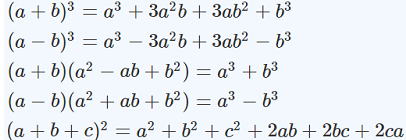
| 例 次の方程式を解いてみよう (1) (3) (5) |
ヒント
(1) 以下の公式を使いましょう。
公式を使わなくても解答できますが、できたら公式を使ってください。
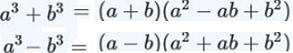
答 (1) (x+2)(![]() ) に因数分解できますが、
) に因数分解できますが、
![]() をさらに因数分解しましょう。
をさらに因数分解しましょう。
![]() …答
…答
(2) ![]()
![]() をさらに因数分解
をさらに因数分解
(3) ![]() 4を2次式に置き換えてみよう。例えば
4を2次式に置き換えてみよう。例えば ![]() 2=a から
2=a から ![]() 4= a2
4= a2
![]() 2=a a=3 ,-1 x2=3, -1より x=±√3 x=i
2=a a=3 ,-1 x2=3, -1より x=±√3 x=i
(4) x=-1, 3, -1±3i …答
(5) 問(3) と同じように、 ![]() 4を2次式に置き換えてみよう。
4を2次式に置き換えてみよう。
![]() と置くと,
と置くと, ![]()
![]()
![]() を元に戻して、
を元に戻して、![]() 2=9,
2=9, ![]() 2=-2
2=-2
![]() …答
…答
(6)![]() から
から ![]() =1,ー1,3
=1,ー1,3
| 問 次の方程式を解きなさい。 (1) (3) |
(1) x=2, -1±√3i (2) (x-3)3 よりx= 3 (3) x=-1, 2±2√2
3. ![]() (割り算)
(割り算)
例題 |
解説
(1) (2)
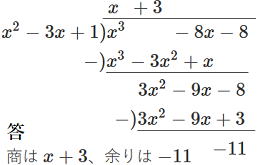
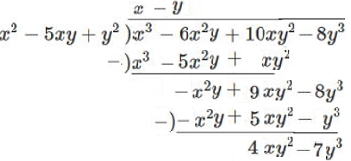
商は ![]() 余り
余り ![]()
(3)解説
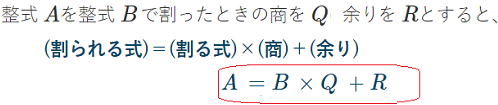
この式がどのように成り立っているか、仮に13を4で割った式で考えてみよう。
13÷4=3 余り1ですね。
A=13, B=4, Q=3, R=1を代入してみましょう。
13÷4=3 余り1 13=4×3+1 で A = B×Q+R ですね。
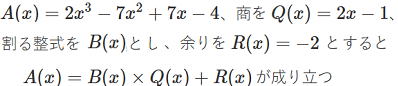
それでは上の例題3を解いてみましょう。
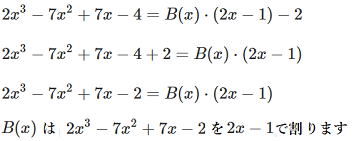
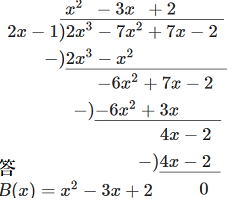
別解 ![]() なので割る数と商を入れ替えて、
なので割る数と商を入れ替えて、
![]() ÷
÷![]() のように
のように
そのまま計算しても結果は同じですね。
| 問 (1) (2) |
答 (1) (2)
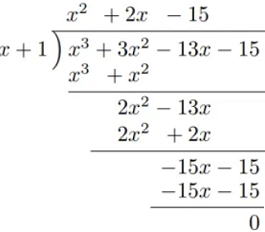

因数定理
| 例 |
![]() とおいて、
とおいて、![]() =1はNG
=1はNG ![]() =2もNG
=2もNG ![]() =-1はOK
=-1はOK
よって、(![]() +1)を因数にもつ方程式
+1)を因数にもつ方程式
![]()
= ![]() より
より
![]() …答
…答
| メモ |
因数分解の公式(形で覚えよう。数多く問題を解くことで慣れます)
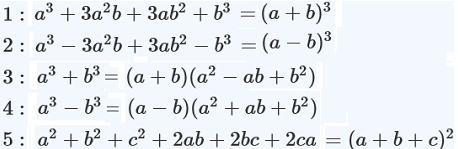
![]() 、
、![]() の代わりに、下の公式のように
の代わりに、下の公式のように![]() 、
、![]() でもおなじですね。
でもおなじですね。
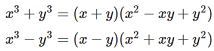
| 例題 (1)から(2)は方程式を解き、(3)から(5)は因数分解しなさい (1) (3) |
答 (1) ![]() (2)
(2) ![]() より
より ![]()
(3)![]() (4)
(4) ![]()
(5)![]()
| 練習問題1 次の式を展開しなさい。 (1) (3) |
答 (1) ![]() (2)
(2) ![]()
(3) ![]() (4)
(4) ![]()
| 練習問題2 次の式を因数分解しなさい。 (1) (3) |
(1)![]() (2)
(2)![]() (3)
(3)![]()
(4)![]() (5)
(5)![]() (6)
(6)![]()
| 例 |
![]() の展開式の一般項は
の展開式の一般項は ![]() ※rは0から始まる
※rは0から始まる
![]() の項は
の項は![]() のときだから
のときだから ![]()
よって、求める係数は ![]()
![]()
| 例題 |
解き方 こうした問題は ![]() や複素数の分数式
や複素数の分数式 ![]() と同じで
と同じで
![]() や
や ![]() を一つの塊(ブロック)として考えることが大切です。
を一つの塊(ブロック)として考えることが大切です。
![]() も同じように
も同じように ![]() のように、一つの塊として考えましょう。
のように、一つの塊として考えましょう。
分母が異なる![]() の計算と同じように、分母を合わせて、
の計算と同じように、分母を合わせて、
![]()
![]() … 答
… 答
問1 次の式を計算しなさい。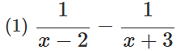 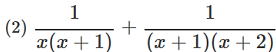 |
答 (3)の問いは分母が同じ ![]() それに、
それに、
(1)や(2)(4)の問いは分母が異なる![]() の計算と同じだね。
の計算と同じだね。
(1) 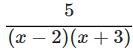 (2)
(2) 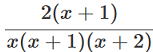 =
=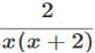
(3) ![]()
(4)![]()
![]()
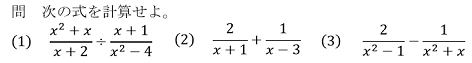 |
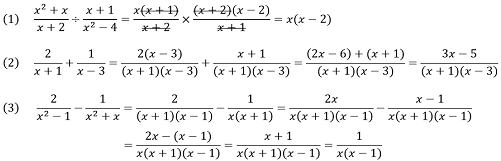
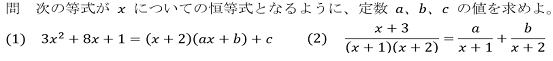 |
解答(1)
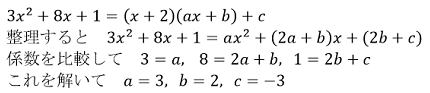
解答(2)
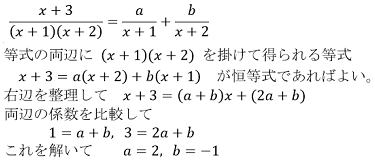
| a+b+c+d=0 のとき,a3+b3+c3+d3=3(a+d) (b+d)(c+d) が成り立つことを証明しなさい。 |
まずa3+b3を考えましょう。以下のように(a+b)3 として、過不足を調整します。
a3+b3=(a+b)3-3(a2b+ab2)
a3+b3+c3+d3=(a+b)3-3(a2b+ab2)+(c+d)3-3(c2d+cd2) …①
a3+b3+c3+d3=(a+b)3-3(a2b+ab2)+(c+d)3-3(c2d+cd2)
=(a+b)3-3ab(a+b)+(c+d)3-3cd(c+d)
条件 a+b+c+d=0より a+b=-(c+d)
右辺に代入
(a+b)3-3ab(a+b)+(c+d)3-3cd(c+d)
= -(c+d)3-3ab{(-(c+d)}+(c+d)3-3cd(c+d)
= -(c+d)3-3ab{(-c-d)}+(c+d)3-3cd(c+d)
= -3ab{(-c-d)}-3cd(c+d)
= 3ab{(c+d)}-3cd(c+d)
= 3(c+d)(ab-cd) …②
条件 a+b+c+d=0より c=-(a+b+d) ②に代入
3(c+d)(ab-cd)=3(c+d)(ab-{-(a+b+d)・d }
=3(c+d)(ab+(a+b+d)d}=3(c+d)(ab+ad+bd+d2)}
=3(c+d){a(b+d)+d(b+d)}
=3(c+d){a(b+d)+d(b+d)} =3(a+d)(b+d)(c+d)}
a3+b3+c3+d3==3(a+d)(b+d)(c+d)} が成り立つ
![]()
相加平均と相乗平均
2つの正の実数![]() ,
,![]() に対して
に対して
![]() を相加平均
を相加平均 ![]() を相乗平均 という。
を相乗平均 という。
また、相加平均と相乗平均のあいだには、次の不等式が成り立つ。
![]() あるいは両辺を2倍して
あるいは両辺を2倍して![]()
(等号が成り立つのは![]() =
=![]() のときである)
のときである)
|
相加平均と相乗平均の大小関係」 a=bのとき,(相加平均)=(相乗平均)・・・・・・② |
| 例 |
解説 相加平均と相乗平均の関係(相加平均≧相乗平均)を用いよう。
![]() であるから
であるから
![]()
![]() より、
より、
![]() よって
よって ![]()