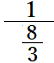5章 データの分析
■中央値の求め方
![]() 戻る
戻る
5章 データの分析
■中央値の求め方
| 【中央値の求め方】 ※ データの数が奇数と偶数個の場合では異なります。 (データの数が奇数個と偶数個の場合の求め方の違い) 【中央値】 例えば1~9まで奇数個、データがあるとき 1 2 3 4 ⑤ 6 7 8 9 中央値は5ですね。 1~10まで偶数個、データがあるとき 1 2 3 4 ⑤ ⑥ 7 8 9 10 5と6が挟まれましたね。 この場合、(5+6)の値を2で割ります。 5.5 になりますね。これが中央値です。 図で再度見てみましょう 偶数のとき 〇○○○●●〇○〇〇 奇数のとき 〇○○○○●〇○○〇〇 ☝ ☝ |
|
| 例題1 右の表はAさんの走り幅跳び20回の記録です。 中央値を求めなさい。 |
|
解説 20個の資料の中央値なので、10番目と11番目の平均をとります。
10番目の値は、4.40~4.50の階級の中にあるので、階級値は4.45
11番目の値も、4.40~4.50の階級の中にあるので、階級値は4.45
この2つの値の平均が求める中央値で 4.45
| 例題2 以下の表はあるクラス30人の英語テストの記録です。 中央値を求めなさい。
|
解説 30個の資料の中央値なので、15番目と16番目の平均をとります。
15番目の値は、60~80の階級の中にあるので、階級値は70。
16番目の値は、40~60の階級の中にあるので、階級値は50。
この2つの値の平均が求める中央値で 60…答
| 問 1~9まで(奇数個)データがあるときの中央値は また、1~10まで偶数個、データがあるときの中央値は |
解説
1 2 3 4 5 6 7 8 9 5…答
1~10まで偶数個、データがあるとき
1 2 3 4 5 6 7 8 9 10 5と6が挟まれましたね。
この場合、(5+6)・2= 5.5 になります。 5.5…答
【四分位数】
「
データの数で4等分した時の区切り値のことです。
4等分すると3つの区切りの値が得られ、小さいほうから「25パーセンタイル(第一四分位数)」
「50パーセンタイル(中央値=第二四分位数)」、「75パーセンタイル(第三四分位数)」とよびます。
また、75パーセンタイル(第三四分位数)から25パーセンタイル(第一四分位数)を引いた値を
「四分位範囲」とよびます。図にして説明しましょう。
| データ数が偶数のとき(上図) データ数が奇数のとき(下図) ①データの値を小さい順に並べます。次に中央値を境にデータを2つに分けます。中央値を第2四分位数といいます。 ②最小値を含む方のデータの中央値を第1四分位数といい、 ③最大値を含む方のデータの中央値を第3四分位数といいます。 ③と②のあいだ、つまり、第3と第1四分位数のあいだにデータの個数のほぼ半分が含まれます。 ④ (第3ー第1)四部位数が四分位範囲です。③-② また、四部位範囲を2で割った値を四分位偏差といいます。 |
 |
なんだか、ややこしい。イヤになってきますね。でも、ここでへこたれてはいけない。
これは便利で、統計や経済等々、データ分析で幅広く用いられています。
具体的に考えていきましょう。
![]()
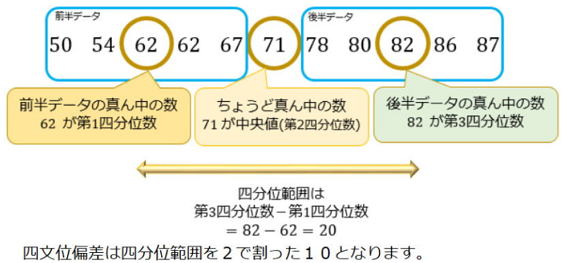
11人の数学のテストをミスった順に並べてみました。(100点満点)
四分位数を求めてみよう。
まず中央値を探し、前半と後半に分けてみましょう。
![]()
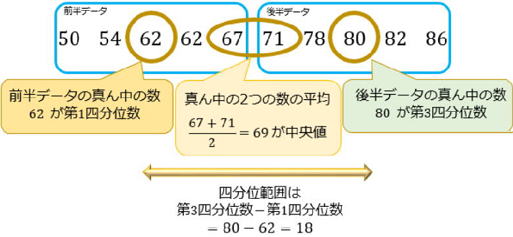
11人の奇数人数でしたが、今度は10人の四分位数を求めてみましょう。
 |
問 以下の表はバスケットボールのAさんの最近10試合の成功したシュートの本数です。
シュートの本数の ①第1四分位数 ②第2四分位数 ③第3四分位数 ④四分位範囲 ⑤四分位偏差を求めなさい。 |
解答) まず、データを小さい順に並べます。
| 3 5 5 6 6 7 7 8 8 10 (単位 本) |
| 3 5 5 6 6❘7 7 8 8 10 (単位 本) |
①第1四分位数=5本 ②中央値は6.5本(第2四分位数) ③第3四分位数=8本
④四分位範囲 8-5=3 ⑤四分位偏差 3÷2=1.5本
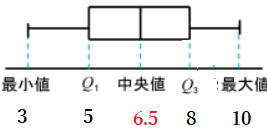
箱ひげ図
次にAさんの成功したシュートの本数の箱ひげ図を作ってみよう。
| 3 5 5 6 6 7 7 8 8 10 (単位 本) |
①第1四分位数=5本 ②第2四分位数 6.5本(中央値) ③第3四分位数=8本
④四分位範囲 8-5=3
これらのデータから以下のようになります。
| 問 下の図はヒストグラムのデータと箱ひげ図の相関関係を表したものです。 (1)から(3)までのヒストグラムは下の箱ひげ図の(A)から(C)までのどれと一致するでしょうか?   |
| 問 次のデータは10人の1週間の自宅学習時間の合計を表したものです。 (1)から(6)までの値を求めなさい。 5, 15, 17, 4, 14, 9, 12, 22, 18, 11 (1) 第1四分位数 (2)第2四分位数 (3)第3四分位数 (4)四分位範囲 (5) 中央値 (6)箱ひげ図を簡単に書きなさい。 |
答 (1)9 (2)13 (3)17 (4)8 (5)13 (6) 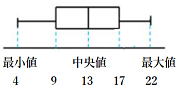
■分散と標準偏差
データの各値と平均値との差を偏差といいます。
例えば,テストの点数が70点,平均値が50点ならば偏差は70-50=20です.
偏差の2乗の平均値を分散といい.分散はS2で表します
以下の表はA投手とB投手がそれぞれ、最近5試合で奪った三振の個数である。
空欄を埋めてみましょう。A投手は左、B投手は右の表です。p134
|
|
まず、平均値を求めます。偏差は平均値との差でしたね。A投手の平均は30÷5=6,B投手の平均も6。
以下のようになります。
|
|
偏差の2乗の平均値を分散といい.分散はs2で表しましたね。
また分散の正の平方根を標準偏差といい、sで表します。
分散や標準偏差の値はデータ全体の散らばり具合を表す数値で、
その値は0に近いほどデータの個々の値が平均値の近くに分布していることを意味し、
大きいほどデータの個々の値に平均値から離れたものが多くあることを意味しています。
A投手とB投手2人の三振を奪った数は30で平均値もそれぞれ6個と、等しくなりますが、
上の表から散りばりぐあいが2投手のあいだで大きく異なっている(ばらつきがある)ことが分かります。
それでは、2投手のA投手が奪った三振の個数から分散と標準偏差を求めてみましょう。
| A投手 | 三振の個数 | 偏差 | (偏差)2 |
| 1試合目 | 4 | -2 | 4 |
| 2試合目 | 8 | 2 | 4 |
| 3試合目 | 7 | 1 | 1 |
| 4試合目 | 5 | -1 | 1 |
| 5試合目 | 6 | 0 | 0 |
| 計 | 30 | 0 | 10 |
分散と標準偏差は以下の公式から
分散=s2 = 10÷5 = 2
標準偏差=s =![]() =1.4142 = 1.41個 となります。
=1.4142 = 1.41個 となります。
偏差 (データの個々の値)-(平均値)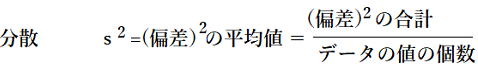 |
| 問1 それでは、投手Bが奪った三振の個数から分散と標準偏差(四捨五入して少数第二位まで) を求めてください。 問2 A投手とB投手が奪った三振の個数の標準偏差を比べて、 どちらの散りばりぐあいが大きいか答えなさい。
|
答 分散=s2 = 50÷5 = 10
標準偏差=s =![]() = 3.16個
= 3.16個
(A投手の標準偏差=s =![]() =1.4142 = 1.41個でした)
=1.4142 = 1.41個でした)
分散や標準偏差はB投手の方が大きく、三振を奪う数にムラがあることが分かります。
以下、再確認しましょう。
偏差の2乗の平均値を分散といい.分散はS2で表しましたね。
また分散の正の平方根を標準偏差といい、Sで表します。
分散や標準偏差の値はデータ全体の散らばり具合を表す数値で、
その値は0に近いほどデータの個々の値が平均値の近くに分布していることを意味し、
大きいほどデータの個々の値に平均値から離れたものが多くあることを意味しています。
| 問1 次のデータは朝テストの5人のデータである。分散と標準偏差を求めよ。 4 8 7 5 6 (10点満点) |
解説 まず、平均値を求めよう。
| データ | 偏差 | 偏差の2乗 |
| 4 | -2 | 4 |
| 8 | 2 | 4 |
| 7 | 1 | 1 |
| 5 | -1 | 1 |
| 6 | 0 | 0 |
| 30 | 0 | 10 |
平均値 30÷5=6 表より
分散=s2 = 10÷5 =2 標準偏差=s =![]() = 1.414 ≒1.41
= 1.414 ≒1.41
| 問2 次のデータの分散と標準偏差を求めよ。 9 10 8 11 7 |
平均値 45÷5=9 よって分散は
{(9-9)2+(10-9)2++(8-9)2++(11-9)2+(7-9)2}÷5=2
標準偏差= ![]() ≒1.4142… 約1.4
≒1.4142… 約1.4
▲相関関係
数学、英語、国語3教科のAくんからFくん6人の試験結果をまとめてみました。
数学と他の教科のあいだになんらかの関係があるか調べることにしましょう。
点数は以下のとおりです。

横軸に数学、縦軸に英語と国語の点数を点で打っていきましょう。(散布図)
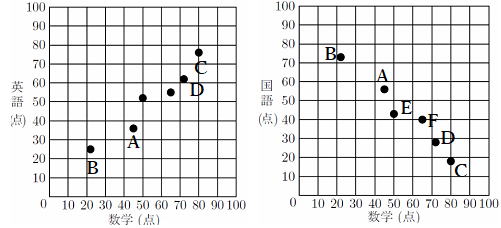
正の相関関係 負の相関関係
2つの相関図から数学ができる生徒は英語ができるといった相関関係が読み取れるが、
数学ができるから国語ができるといったことはいえず、相関図から読み取れるのは
相関関係であって因果関係(xだからyといった原因と結果)ではないといえる。
r=-1、r=0、r=1に注視!
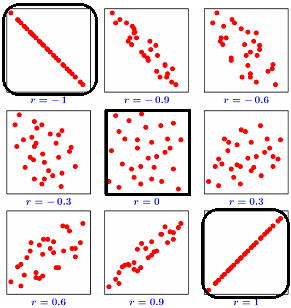 r:相関係数
r:相関係数
上の散布図を相関係数(r)のマイナス(-1)からプラス(1)まで並べてみます。
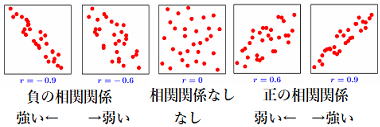
問 相関係数①から③は右図のどれに当るでしょう。 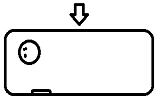 ( ) ( ) ( ) |
▲相関係数
次に、実際に、相関係数を求めてみよう。
まず、相関関係を調べたい2つのデータの値を![]() とします。
とします。![]() の偏差と
の偏差と![]() の偏差の積の平均値を共分散といい、
の偏差の積の平均値を共分散といい、
共分散を![]() の標準偏差と
の標準偏差と![]() の標準偏差の積で割った値を相関係数といいます。
の標準偏差の積で割った値を相関係数といいます。
相関係数は記号![]() で表します。 以下の式が成り立ちます。
で表します。 以下の式が成り立ちます。
共分散= |
| 例 右の表は、5人の生徒の先月の読書時間と読んだ本の冊数を示したものです。 読書時間と読んだ本の冊数の相関係数を求めてみましょう。 |
|
解説 読書時間を![]() とし、読んだ本の冊数を
とし、読んだ本の冊数を![]() とします。
とします。
上の表から ![]() の平均値=(5+8+9+12+11)÷5=9時間
の平均値=(5+8+9+12+11)÷5=9時間
![]() の平均値=(2+6+4+8+5)÷5 = 5冊
の平均値=(2+6+4+8+5)÷5 = 5冊
| 生徒 | |
( |
( |
偏差の積 | |||
| A | 5 | 2 | -4 | -3 | 16 | 9 | 12 |
| B | 8 | 6 | -1 | 1 | 1 | 1 | |
| C | 9 | 4 | 0 | -1 | 0 | 1 | |
| D | 12 | 8 | 3 | 3 | 9 | 1 | |
| E | 11 | 5 | 2 | 0 | 4 | ||
| 計 | 45 | 25 | 0 | 0 | 30 | 20 | 20 |
共分散=![]() と
と![]() の偏差の積の平均値
の偏差の積の平均値
 でしたね。
でしたね。
![]() 、
、![]() の共分散=20/5=4
の共分散=20/5=4
![]() の標準偏差=√30/√5=√6
の標準偏差=√30/√5=√6
![]() の標準偏差=√20/√5=2 よって、
の標準偏差=√20/√5=2 よって、
相関係数r=4/(√6×2)=2/√6=√6/3=0.816
ーー中間・期末対策(基本まとめ問題)ーー
| 問1 以下の表はある会社の男子、女子社員、それぞれ9人について、体重を小さい順に示したものです。男子社員、女子社員の体重について、次の問いに答えなさい。 (1)四分位数を求めなさい。 (2)四分位範囲を求めなさい。 (3)四分位偏差を求めなさい。
|
(1)四分位数
| 男子(kg) | 55 | 56 | 57 | 59 | 62 | 64 | 69 | 75 | 89 |
第2四分位数 62 第1四分位数 (56+57)÷2=56.5
第3四分位数 (69+75)÷2=72
| 女子(kg) | 42 | 44 | 45 | 47 | 51 | 53 | 55 | 58 | 62 |
第2四分位数 51 第1四分位数 (44+45)÷2=44.5
第3四分位数 (55+58)÷2=56.5
(2)四分位範囲 男子: 72-56.5=15.5 女子:56.5-44.5=12.0
(3)四分位偏差 男子: 15.5÷2=7.75 女子:12÷2=6
|
問2 問1で求めたデータを使って、次の問いに答えなさい。(単位:Kg)
(2)箱ひげ図で表しなさい。  |
答
(1) 5数要約で表すと(単位:Kg)
| 最小値 | 第1四分位数 | 第2四分位数 | 第3四分位数 | 最大値 | |
| 男子 | 55 | 56.5 | 62 | 72 | 89 |
| 女子 | 42 | 44.5 | 51 | 56.5 | 62 |
(2)箱ひげ図は
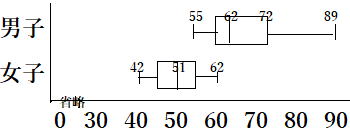
|
問3 下の表は、ある生徒5人について、数学と国語の小テストの得点を示したものである。次の問いに答えなさい。
(1) 数学と国語の小テストの得点について、それぞれの平均値を求めなさい。 |
(1) 数学の平均値 (6+2+9+3+10)÷5=30÷5=6
国語の平均値 (6+5+4+7+8)÷5=6
(2) それぞれの分散と標準偏差
数学の分散 {(6-6)2+(2-6)2+(9-6)2+(3-6)2+(10-6)2} ÷5
=(0+16+9+9+16)÷5=10 分散:10
数学の標準偏差 √10 ≒3.162 標準偏差:3.2
国語の分散 {(6-6)2+(5-6)2+(4-6)2+(7-6)2+(8-6)2} ÷5
=(0+1+4+1+4)÷5=2 分散:2
国語の標準偏差 √2 ≒1.414 標準偏差:1.4
|
問4 次の表は、ある高校の女子10人について、垂直とびと走り幅とびの記録を示したものである。次の問いに答えなさい。
|
答 (1)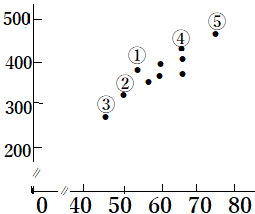
(2)全体的に点の分布が右上がりになっているから
「垂直とびの高さが高い生徒は走り幅とびの距離も長い」相関関係にある傾向が読み取れる。
別解)垂直とびの高さと走り幅とびの距離は正の相関関係があるといえる。
| 問5 次の資料は5人の生徒の1週間の学習時間である。分散と標準偏差を求めなさい。 11, 5, 8, 9, 17 (単位:時間) |
答 平均値=50÷5=10
| 生徒 | データ(時間) | 偏差 | (偏差)2 |
| A | 11 | 1 | 1 |
| B | 5 | -5 | 25 |
| C | 8 | -2 | 4 |
| D | 9 | -1 | 1 |
| E | 17 | 7 | 49 |
| 計 | 50 | 0 | 80 |
分散は80÷5=16 標準偏差 4時間
問6 次の表は6人の生徒の数学と英語の小テストの得点を示したものである。表を完成させ、数学の得点
|
解答 ![]() の平均値=42/6=7
の平均値=42/6=7 ![]() の平均値=36/6=6
の平均値=36/6=6
| 生徒 | |
|
|
( |
( |
偏差の積 | |
| a | 8 | 6 | 1 | 0 | 1 | 0 | 0 |
| b | 6 | 4 | -1 | -2 | 1 | 4 | 2 |
| c | 4 | 5 | -3 | -1 | 9 | 1 | 3 |
| d | 9 | 7 | 2 | 1 | 4 | 1 | 2 |
| e | 7 | 9 | 0 | 3 | 0 | 9 | 0 |
| f | 8 | 5 | 1 | -1 | 1 | 1 | -1 |
| 計 | 42 | 36 | 0 | 0 | 16 | 16 | 6 |