■加速度
1秒当たりの速度の増分 単位時間あたりの速度の変化
作業中
正の加速度 負の加速度

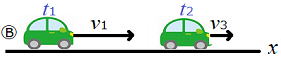
図Ⓐは加速している場合(正の加速度) 図Ⓑは減速している場合(負の加速度)
物理 戻る
■加速度
1秒当たりの速度の増分 単位時間あたりの速度の変化
作業中
正の加速度 負の加速度


図Ⓐは加速している場合(正の加速度) 図Ⓑは減速している場合(負の加速度)
| 問 物体が直線上を運動している。 この物体は,スタートしてから2.0秒後には22m移動し, スタートしてから10秒後には1.0✕102m移動した。スタートから10秒間の平均の速さを求めよ。 また,スタートから2.0秒間の平均の速さを求めよ。 |
10m/s ,11m/s
| 問1 東西方向に延びる道路上を,Aは東向きに4.0m/sで,Bは東向きに7.0m/sで進んでいる。 Aから見たBの相対速度を求めよ。 また,Bから見たAの相対速度を求めよ。 |
相対速度=相手の速度−自分の速度 と考えると分かりやすい。
下の図でAから見たBの相対速度はAが自分の速度なので7.0−4.0=3.0m/s となります。
| 解説 右図のようにx軸を東にとると、Aは4.0m/s、Bは7.0m/sで進んでいるので、Aから見たBの相対速度は東向きに7.0−4.0=3.0m/s Bから見たAの相対速度は4.0−7.0= −3.0 西向きに3.0m/s |
| 問2 x軸上を,Aは−12m/sで,Bは8.0m/sの速度で進んでいる。Aから見たBの相対速度を求めよ。 また,Bから見たAの相対速度を求めよ。 |
| 答 Aから見たBの相対速度:8.0−(−12)=20m/s Bから見たAの相対速度:−12−8.0=-20m/s |
| 問3 線路沿いの道路を北向きに15m/sで走る車から,線路上の電車を見たところ, 南向きに5.0m/sで運動しているように見えた。 静止している人から見た電車の速度を求めよ。 |
北向きを正とする 10m/s →
▲等加速度直線運動
v=v0+at x=v0t+![]() at2 v2-v02=2ax (前の2つの公式から導きだせる)
at2 v2-v02=2ax (前の2つの公式から導きだせる)
| 問 x軸上を運動する物体がある。原点0から初速度6.0m/s, 加速度2.0m/s2で出発した。 (1)出発してから3.0秒後の物体の速度を求めよ。 (2)出発してから3.0秒後の物体の位置を求めよ。 |
解説)
x軸上を正の方向に進んでいるということは問題には書いていませんが、加速度が正の値で与えられているので、
正の方向に進んでいると判断します。
「原点での初速度が6.0m/s」なので斜面を球が転がる場合で、原点の手前から転がっていたか、
力を加えて初速度をつけて転がし始めたイメージしておけば良いでしょう。
速度は2.0m/s増え,3秒間では6.0m/s増えることになります。よって
(1)この物体の3秒後の速度は、初速度に増えた速度を加えて、
v=6.0+6.0=12.0m/s 初速度v0=6.0m/s 加速度2.0m/s2 時間t=3 これを公式に代入
v=6.0+6.0=12.0m/s
(2) 公式 x=v0t+![]() at2 から
at2 から
x=6.0×3+![]() ×2.0×9=27m
×2.0×9=27m
【高校物理】「v-tグラフ(等加速度直線運動)」(練習編) | 映像授業のTry IT (トライイット) (try-it.jp)
▲自由落下
v0=0(初速度) a=g (重力加速度) ※落下させる位置(速度も加速度も0)
v=gt y=![]() gt2 ※上下運動なので軸をyとした。v2=2gx
gt2 ※上下運動なので軸をyとした。v2=2gx
▲鉛直投げ上げ
※重力に逆らって投げ上げため加速度gは負に働く (g=9.8m/s2)
v=v0-gt y=v0t-![]() gt2 v2-v02=-2gx
gt2 v2-v02=-2gx
| 例題 橋の上から小石を自由落下させると、3.0秒後に水面に達した。 ①水面に達する直前の速度を求める。 v=gtより v=9.8×3.0=29.4m/s ②水面から橋までの高さを求めよう。 y= |
| 問 ビルの屋上から初速度19.6m/sで鉛直上向きに小球を投げると、地面に達するのに6.0秒かかった。 ①最高点に達するまでの時間を求めなさい。 ②地面に達する直前の速度を求めなさい。 ③ビルの高さを求めなさい。 |
ビルの屋上から初速度19.6m/sで鉛直上向きに小球を投げると、地面に達するのに6.0秒かかった。
①最高点に達するまでの時間
重力に逆らって投げ上げたので負の加速度、速度が0になったら正の加速度に変わるので
v=v0-gt 0=19.6−9.8t t=2.0s
②地面に達する直前の速度
v=v0-gtより v=19.6-9.8×6=-39.2 39m/s 鉛直下向き
③ビルの高さ
y=v0t-![]() gt2より y=19.6×6-
gt2より y=19.6×6-![]() ×9.8×62 =-58.8 58.8m
×9.8×62 =-58.8 58.8m
| 問1 エレベータが1階から鉛直上向きに動き出した。はじめの5.0s間は大きさ1.2m/s2の 一定の加速度で動き、次の10s間は一定の速度で動いた。その後、6.0s間は一定の加速度で 減速して止まった。 ⑴ エレベータの速さの最大値はいくらか。 ⑵ 最後の6.0s間の加速度の大きさはいくらか。 (3) 動き出してから止まるまでにエレベータは何m上昇したか。 |
| 解答 問題のイメージがつかめなかったら図を書こう。次にvtグラフ。 5.0s間は一定の加速度1.2m/s2だから傾きも1.2 ⑴ エレベータの速さの最大値は 座標(5,6)で6m/s …答 ⑵ 最後の6.0s間の加速度の大きさは 傾き-(6/6) =-1.0m/s2 ここで注意‼ 加速度の大きさだから 1.0m/s2 …答 (3) 動き出してから止まるまでにエレベータは何m上昇したか。 1⃣+2⃣+3⃣の台形の面積={(10+21)×6}÷2= 93m…答 |
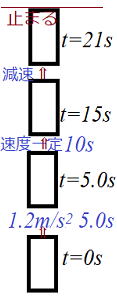 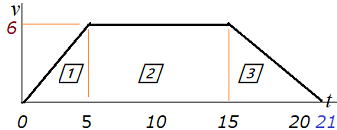 |
| 問5 鉛直上向きに一定の速さ14m/sで上昇する気球から、小球を静かに手から離したところ、 10s後に地面に達した。 重力加速度 9.8m/S2として各問いに答えよ ⑴地面で静止している人から見ると、離した直後の小球の速さはどちら向きに何m/sか ⑵小球を離した高さは、地面から何mか |
答 ⑴鉛直上向き 14m/s ⑵3.5×102m
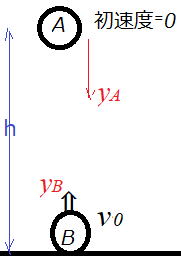
| 例題 高さhの位置から静かに離した物体Aと同時に、地面から物体Bを鉛直上向きに 速さvで投げ上げたところ、2つの物体は同時に地面に達した。 このときのvは重力加速度をgとしてg, hでどのように表すことができるか、考えてみよう。 解説 A:自由落下運動 B:鉛直投げ上げ 同時に地面に達するまでの時間をtとする。 小物体Aの落下距離をyAとおくと、 公式から 自由落下なので初速度v0は0 yA = h = いっぽう小物体Bは yB= v0t- h= v0t なので, t= ③式を①に代入 yA= よって h=gh2/2v02 |
 |
応用
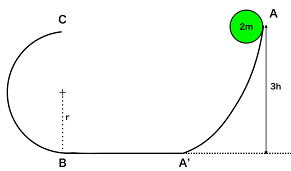
| 問題2: いま、以下の図のように質量2mの”小球”が高さ3hの点Aにある。BC間は半円になっておりその半径をrとする。 点Aから点A'、点A'から点B、点Bから点Cまでは滑らかにつながっており、摩擦力が働かないものとする。このとき以下の(1),(2),(3)の問いに答えなさい。(重力加速度はgとする) (1):Bにおける球の速度VBとBを通過する直前に球が水平面から受ける力(=垂直抗力)を求めよ。 (2): Bを通過した直後に球が水平面から受ける垂直抗力を求めよ。(このときVBを使用して良い) (3): 点Cまで小球が曲面BCを離れることなく達した。この時、点Cで小球が落下しない『r』の条件を示せ。 |
 |
解説
力学的エネルギー保存則、力のつりあい、円運動(遠心力)などが組み合わさった問題です。
垂直抗力Nの意味
まずVBについて。摩擦がないので、Aでの位置エネルギーがすべてBでの運動エネルギーに変換されますね。
したがって、力学的エネルギー保存則より ![]()
次にBを通過する【直前】の垂直抗力を求めましょう。
(※重要ポイント!): 「直前」と「直後」では全く異なります。
「直後」では、円運動に入るために遠心力を考慮する必要があります。
それに対し、「直前」では、単に重力と垂直抗力という二つの鉛直方向の力のみを考えれば良いので、
2mg…答 以下、リンクを張ってますのでご覧ください。
円運動と遠心力・垂直抗力をジェットコースターの問題で解説 (linky-juku.com)
ツール:![]()
![]()
![]()
![]()
![]()
![]()