頂点が原点(0,0)の二次関数グラフは中学3年で学習しました。思い出してください
下のグラフは２次関数。つまり、
は
の２乗に比例するグラフ。y=ax2で表します。仮に比例定数
＝２として、y=2x2のグラフを書いてみましょう。
のようなグラフになりますa＞0：下に凸の場合と、a<0：上に凸の場合の２つでしたね。
高校ではx軸やy軸に平行移動したグラフを学習していきます。
二次関数のグラフ 二次不等式 戻る
頂点が原点(0,0)の二次関数グラフは中学3年で学習しました。思い出してください
下のグラフは２次関数。つまり、はの２乗に比例するグラフ。y=ax2で表します。
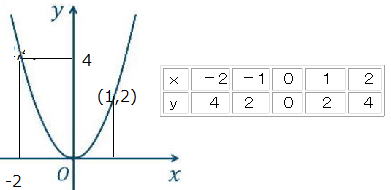
仮に比例定数＝２として、y=2x2のグラフを書いてみましょう。
のようなグラフになります
a＞0：下に凸の場合と、a<0：上に凸の場合の２つでしたね。
高校ではx軸やy軸に平行移動したグラフを学習していきます。
|
以下、基本的な二次関数グラフです。  |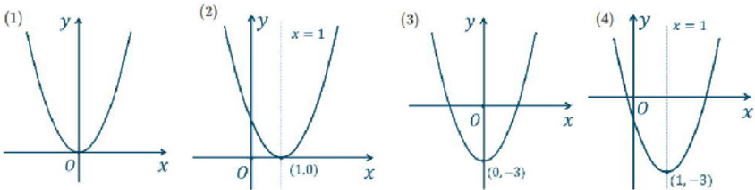
| （１）のグラフは中学で学習したy=ax2のグラフで、仮にa=２とし、y=２x2のグラフとしましょう。 （２）のグラフはy=２x2のグラフをx軸に平行に+１移動したグラフです。 （３）のグラフはy=２x2のグラフをｙ軸に平行に−３移動したグラフです。 （４）のグラフはy=２x2のグラフをx軸に平行に+１移動、y軸に平行に−３移動したグラフです。 なお、（４）のグラフはい一般的に y = (x－p)2+q で表します。頂点がすぐわかるからです。 |
具体的に説明しましょう。
y= x2－４x－１２
まず中学で学習した[乗法の公式]を使います。
y= x2－４x－１２の y= x2－４xに注目。
y= (x−２)2になり４が余計になりますので４を引きます。
y= (x−２)2－4－１２ で y= (x−２)2−１６でＯＫ。グラフの公式に変形できました。
x軸に平行に２、y軸に平行に－１６、平行移動したグラフで、頂点（２，－１６）ですね。
グラフを書く際にはy軸との接点も必要ですね。
y軸との接点はxが０のときですから、（０，－１２）でy軸と接しますね。
| 例題 y= x2＋４x＋２のグラフを書き、頂点およびy軸との接点を答えなさい。 |
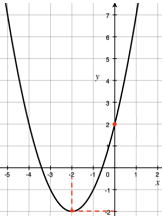
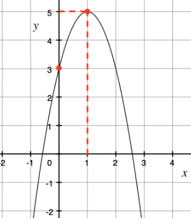
| 問 y= −２x2＋４x＋３のグラフを書き、頂点およびy軸との接点を答えなさい。 |
| 問１ ①２次関数 y= －x2 ＋ ４x＋２の最大値、または最小値を求めなさい。 ②２次関数 y= －x2 －６x－４の最大値、または最小値を求めなさい。 問２ ２次関数 y=－ x2＋６x＋cの最小値が−４のとき、定数cの値を求めなさい。 |
問１-① y= －x2 ＋ ４x＋２
y= －(x2−４x)＋２ y= －(x−２)2＋４＋２ y= －(x−２)2＋６
a＜０でxの範囲も指定されてないので最大値のみ
頂点（２，６）だから 最大値は６ （x=２のとき）
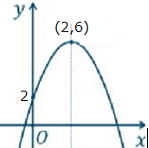
問１-② y= －(x＋３)2＋５ 最大値は５ （x=－３のとき）
問２ y= x2＋６x＋Ｃ
y= (x＋３)2−９＋c
a＞０だから 頂点は（－３，−９＋c）
x = －３で 最小値 −９＋c = −４
c =−４＋９ c =５
| 問３ f(x) =－２x2＋ax＋３について、f(x) = −３ を満たしているとき、次の(１)～(３)の問いに答えなさい。 (1) aの値を求めなさい。 (2) ２次関数 y=f(x)のグラフの軸と頂点を求め、そのグラフをかきなさい。 (3) ２次関数 f(x)において、定義域が−１以上、２以下のときの最大値と最小値を求めなさい。またそのときのxの値は？。 |
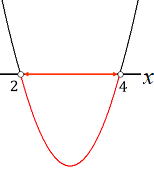
| x2−６x＋８＜０ を考えてみます。グラフを意識し、 y=x2−６x＋８とおいてみましょう。y=(x−4)(x−2) x軸で交わる２次関数グラフを書いてみます。(右図) xは２と４で交わり、y＜０, つまりx2−６x＋８＜０ ですのでx軸よりマイナス、下の領域(赤の個所)になります。 ２＜x＜４…答 |
 |
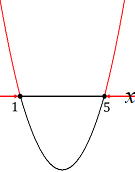
| 例２ x2−６x＋５≧０ y=x2−６x＋５をグラフにすると、 右図のようになり、x軸より上になり、 x≦1 ， x≧５ …答 |
 |
| 問 以下の(1)から(4)までの２次不等式を解きなさい。 (1) x2＋x−２＞０ (2) x2−６x−７≦０ (3) ４x2−4x＋１≧0 (4) x2－８x＋１７＜０ |
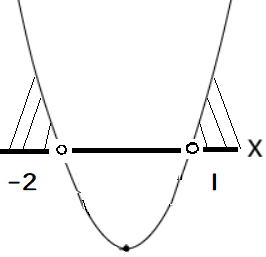
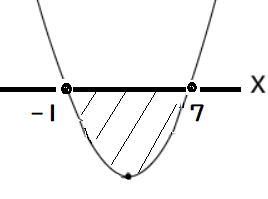
下の図から答は、(1) x＜－２，x＞１ (2) －１≦x≦７
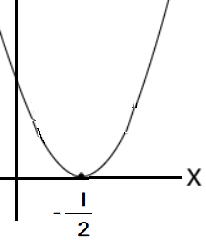
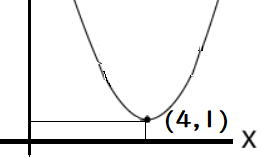
(3) x＝−１/２ (4) xの解無し
| 問 x2＋ax−6＞０の解が x<－1, x>6 のときのaの値を求めなさい。 |
解説 x2＋ax−6を以下のようにグラフの式にします。
－6＞０
軸：
－１と６の中心は2.5
右図より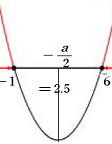 
＝2.5 a＝－５ …答