不定方程式5xー9y=2の整数解を1つ求めると、
x=4,y=2 であるから(x=-5,y=-3でもOK)
5×4ー9×2=2 …②
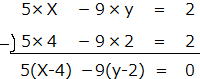
5(xー4)ー9(yー2)=0
5(xー4)
数 A
整数の性質
1節 約数と倍数節 約数と倍数
1. 約数と倍数
・4の倍数の判定法
3桁の数字(自然数)をNとしよう。
N=100a+10b+c と表せる。
=4×25a+(10b+c)
4×25aは4の倍数だから
(10b+c)が4の倍数であればNは4の倍数である。
・3の倍数の判定法と9の倍数の判定法
N=100a+10b+c(自然数)
=(99+1)a+(9+1)b+c
=9(11a+b)+(a+b+c)
9(11a+b)は3及び9の倍数なので
a+b+cが3の倍数であれば、Nは3の倍数であり、
9の倍数であればNは9の倍数である。
このことから倍数の判定ができる
4の倍数の判定法:下2桁が4の倍数である
3の倍数の判定法:各位の数の和が3の倍数である
9の倍数の判定法:各位の数の和が9の倍数である
| 問1 次の数のうち4の倍数はどれか? ①524 ②308 ③582 ④1276 ⑤6334 問2 次の数のうち3の倍数はどれか。また、9の倍数は? ①621 ②705 ③1348 ④1276 ⑤6372 |
答 問1:①,②,④
問2:3の倍数は①,②,④ 9の倍数は①,④
正の約数の個数
16の正の約数の個数を求めてみよう。
16を素因数分解すると、24
よって、16の正の約数の個数は
20,21,22,23,24 つまり1,2,4,8,16,の5個 (20=1)
このことから下のことがいえる。
anの正の約数の個数は1a1a2a3a4…an のn+1(個)である。
| 例 675の正の約数の個数を求めよ。 |
675を素因数分解すると、675=33×52
675の正の約数は
33の正の約数 1,3,32,33の4個の1つと(下図参照)
33の正の約数 1, 5, 52 の3個の1つとの積で表せる。
よって、675の正の約数の個数は4×3=12(個)
| 1(50 ) | 5(51 ) | 52 | |
| 1(30) | 1×1 | 1×5 | 1×52 |
| 3(31 ) | 3×1 | 3×5 | 3×52 |
| 32 | 32×1 | 32×5 | 32×52 |
| 33 | 33×1 | 33×5 | 33×52 |
| 問 432の正の約数の個数を求めよ。 |
答 20
2.最大公約数と最小公倍数
整数の割り算と商 および余り
| 例 整数aを8で割ると6余り、整数bを8で割ると5余る。このとき次の数を8で割ったときの余りを求めてみよう。 (1) a+b (2) ab |
a,bは整数m,nを用いて、
a=8m+6 ,b=8n+5 と表せる。
(1) a+b=(8m+6) + (8n+5)
=8m+8n+11=8(m+n)+11=8(m+n+1)+3
m+n+1は整数である。
よってa+bを8で割ったときの余りは3
(2) ab=(8m+6)(8n+5)=64mn+40m+48n+30)
=8(8mn+5m+6n+3)+6 (8mn+5m+6n+3:整数)
よってabを8で割ったときの余りは6
| 例 整数aを6で割ると5余り、整数bを6で割ると2余る。このとき次の数を6で割ったときの余りを求めよ。 (1) a+b (2) ab (3) bーa |
答 (1) 1 (2) 4 (3) 3 (0≦余り<正の整数)
3.ユークリッドの互除法
24と9の最大公約数は3ですね。たとえば、24と9の最大公約数を求める際、
24÷9=2 余り6
9÷6=1 余り3
6÷3=2 より 3
ただひたすら、割り算を繰り返すことによって求める方法をユークリッドの互除法といい、
24と9では暗算でできますが、大きな2つの数の最大公約数を求めるときに有効になります。
上の例に従って592と222の最大公約数を求めてみよう。
592÷222=2 余り148
222÷148=1 余り74
148÷74=2 最大公約数:74
| 問 互除法を利用して、 (1) 143と26の最大公約数を求めよ。 (2) 187と68の最大公約数を求めよ。 |
(1) 13 (2) 17
4.不定方程式
| 例1 方程式xy=4の整数解をすべて求めてみよう |
x,yがともに4の約数であるから、
x=1, y=4 x=ー1, y=ー4
x=2, y=2 x=ー2, y=ー2
x=4, y=1 x=ー4, y=ー1
したがって4の約数は
1,ー1,2,ー2,4,ー4
| 例2 不定方程式4x+7y=0の整数解をすべて求めてみよう(p:75) |
4x+7y=0から 4x=ー7y …①
4と7は互いに素であるから、xは7の倍数であり、
整数kを用いて x=7k ここでx=7kを①に代入すると、
4×7k=ー7yより y=-4k
よって不定方程式4x+7y=0のすべての整数解は
x=7k,y=-4k (k:整数)
| 問 次の不定方程式の整数解をすべて求めよ (1) 6x+7y=0 (2) 2xー9y=0 (p:75) |
(1) 6x+7y=0 6x=-7y…①
6と7は互いに素で、xは7の倍数であるので、
整数kを用いて、x=7k ここでx=7kを①に代入
6×7k=-7yより y=-6k
よって不定方程式6x+7y=0のすべての整数解は
x=7k,y=-6k (k:整数)
(2) 2xー9y=0 2x=9y …①
2と9は互いに素で、xは9の倍数であるので、
整数kを用いて x=9k ここでx=9kを①に代入
2×9k=9yより y=2k
よって不定方程式2xー9y=0のすべての整数解は
x=9k,y=2k (k:整数)
| 例3 不定方程式5xー9y=2の整数解をすべて求めてみよう(p:77) |
まず、5xー9y=2…① の整数解を1つ求める。
不定方程式5xー9y=2の整数解を1つ求めると、
x=4,y=2 であるから(x=-5,y=-3でもOK)
5×4ー9×2=2 …② 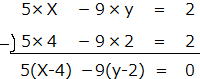
5(xー4)ー9(yー2)=0
5(xー4)