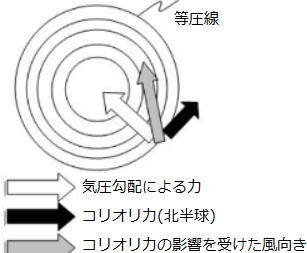
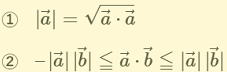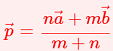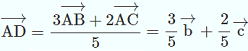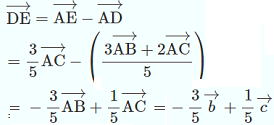低気圧は、周囲より気圧が低いため、その中心(台風の目:赤丸)に向かって 気流(青ベクトル)が流れます。ところが、地球の自転の影響で、北半球では進行方向に向かって、気流の流れに対し右向きの力(黄ベクトル)が働きます。(コリオリの力)
風向きは、気圧の差による流れと、コリオリの力の合成として生じ、右に振られながらも、低気圧の中心に吹き込むため、(ピンクベクトル)のようになり、渦を巻くことになります。
大気だけでなく、海流の運動もコリオリの力の影響を受けています
Tossy's homepageより
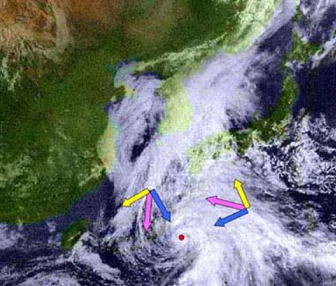
平成15年5月30日の台風4号の気象衛星写真
(写真:高知大学・東京大学・気象庁 より)

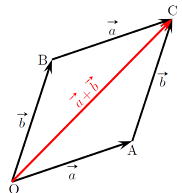
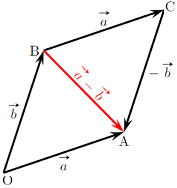
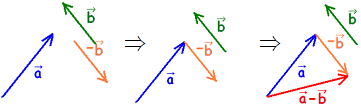
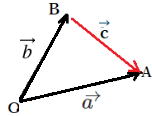
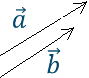
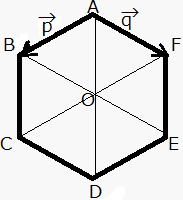
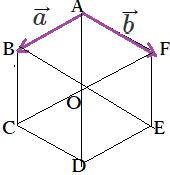
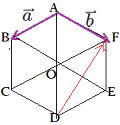
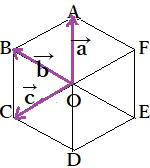
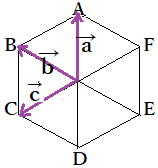
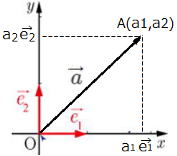
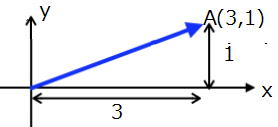
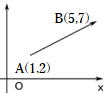
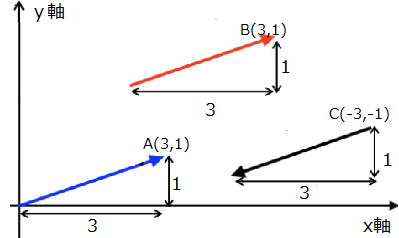
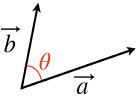


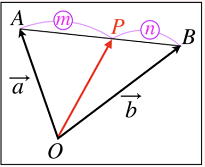
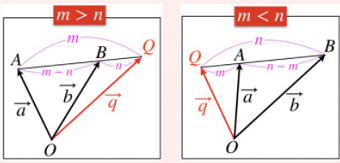
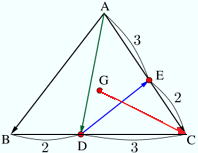
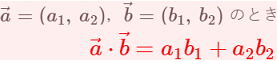 …公式2 と表せる。
…公式2 と表せる。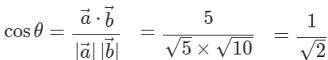
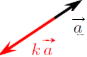
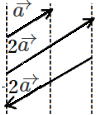
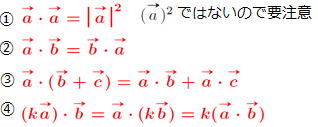 kは実数
kは実数