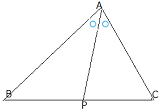
BP:PC=AB:AC
図形の性質
1.三角形と線分の比
角の二等分線と線分の比
| △ABCで、∠Aの二等分線と対辺BCの交点をPとすると、 BP:PC=AB:AC |
 |
| 証明 点Cを通りADに平行な直線を引き、辺BAの延長との交点をPとする。AD∥PCより ∠APC=∠BAD(同位角) ∠ACP=∠CAD(錯角) 工事中(Break time) |
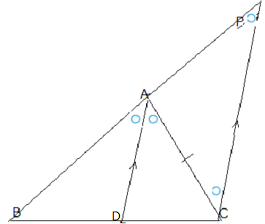 |
| 問 △ABCで、ADが∠Aの二等分線であるとき、線分BDの長さを求めなさい。 BC=10 page90 |
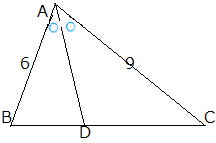 |
答 BD=Xとおく。 X:DC=AB:ACより
X:(10-X)=6:9 9X=6(10-X) X=4
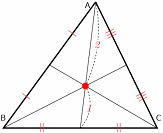
2.三角形の重心・外心・内心
三角形の重心
(①三角形の3本の中線は1点で交わる)
(②重心は、それぞれの中線を2:1に分ける)
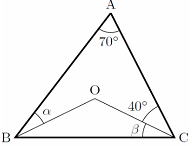
問 点Oは△ABCの外心である。∠αと∠βの角度を求めよ。∠α=30°と∠β=20°
三角形の外心(三角形の3辺の垂直二等分線は1点で交わる)
| 右の図で点Oが△ABCの外心であるとき∠BACの大きさを求めてみよう | 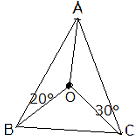 |
解説
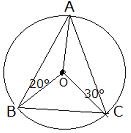 |
点Oが△ABCの外心(円の中心)であるから OA=OB=OC よって△OAB△OACは二等辺三角形となり ∠OAB=∠OBA=20° ∠OAC=∠OCA=30°したがって ∠BAC=∠OAB+∠OAC=20°+30° =50°…答 |
問 点Oは△ABCの外心である。∠αと∠βの角度を求めよ。


解答
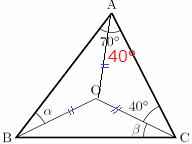 |
∠OAB=30°よって、 ∠α=30°また、三角形の内角の和から 180°=(70°+40°+∠β+∠30°+∠β) 180°=(140°+2β) 2β=40° よってβ=20° |
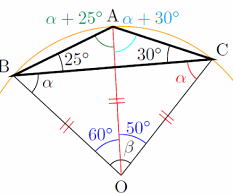 |
∠OCA=α+30°= ∠OCA 同様に ∠OBA=α+25°= ∠OAB △OACについて考えると △OAC=180° 180°=(50°+2(α+30°) 180°=(2α+110°) 2α=70° α=35° またβは β=180°⊸2α β=180°-70°=110° |
三角形の内心(三角形の3つの二等分線は1点で交わる)
| 右の図で点Iが△ABCの内心であるとき、∠BACの大きさを求めてみよう | 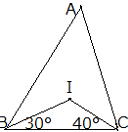 |
解説 外接円を描くことで、おおよその性質が見えてきます。
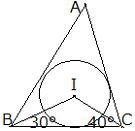 |
IBとICはそれぞれ∠ABC,∠ACBの二等分線であるから ∠ABC=2×30°=60° ∠ACB=2×40°=80° 三角形の内角の和は180°だから ∠BAC=180°⊸(∠ABC+ ∠ACB) =180°⊸(60°+80°)=40° |
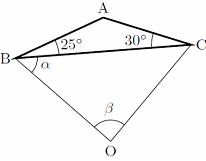
問 下の図で点Iが△ABCの内心であるとき、各α、βの値を求めよ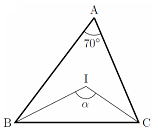 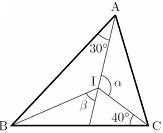 |
内接円を描くことで、おおよその解答へのイメージが見えてきます。
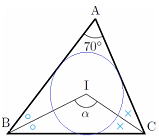 |
∠ABI=∠CBI ∠ACI=∠BCI よって、△ABCで考えると 180°=(∠CBI×2)+∠BCI×2)+70° 2(∠CBI+∠BCI)=110°∠CBI+∠BCI=55° △IBCで考えると 180°= ∠CBI+∠BCI+α α=180°⊸ (∠CBI+∠BCI) α=180°⊸55°=125° |
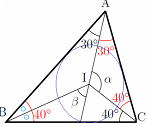 |
∠ACI=40°∠CAI=30° よってαの角度は α=180°⊸70°=110° △ABCで考えると ∠B=2×∠CBIで ∠B=180°⊸ (80°+60°)=40° ∠ABI=20°なので ∠BIA=180°⊸ 50°=130°よって、 β=50° |
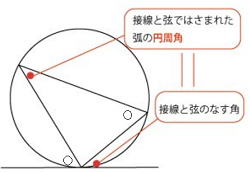
円の接線と弦のつくる角
円の弦と、その弦の一端を通る接線のつくる角は、その角の内部にある弧の円周角と等しい(接弦定理)
問1 ∠x の大きさを求めよ。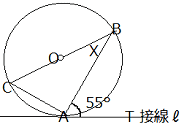 |
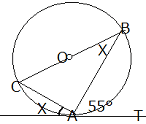
答
∠X=180°- (90°+ 55°) =35°
| 問2 右の図においてPTは円Oの接線でありAは接点。また、BCは円Oの直径である。このとき∠BAP、∠ABCを求めなさい。 | 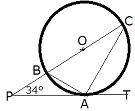 |
分かった情報は図に書き込んでいこう。
BCは直径であるから∠BACは90°
また、接線と弦の作る角の性質より ∠BAP=∠BCA…①
△PACにおいて内角の和は180°だから
∠BCA+34°+(90°+∠BAP)=180°
①から
∠BAP+124°+∠BAP=180°
2×∠BAP=56° よって ∠BAP=28°
∠ABC=180°⊸90°ー28°=62°
方べきの定理
| 円の2つの弦AB,CDの交点(図1)、 または、それらの延長の交点(図2)をPとすると、 PA×PB=PC×PDが成り立つ。 図1 図2 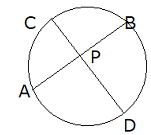 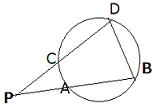 このことは円と直線の交点に作られる2組の三角形が、それぞれ相似であることから証明できます。 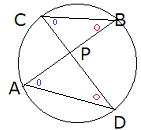 図1 どちらも弧AC、BDの円周角で∠A=∠C、∠B=∠Dから相似 図1 どちらも弧AC、BDの円周角で∠A=∠C、∠B=∠Dから相似 |
問1 下の図において、PAの値を求めよ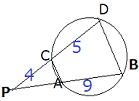 PC=4, CD=5,AB=9 PC=4, CD=5,AB=9 |
PA = x とおく。
方べきの定理より、4・(4+5)=x・(x+9)より、 x2 + 9x = 36 x2 + 9x ⊸ 36 = 0
乗法の公式より、(x ー3)(x +12) = 0
x>0 だから x = 3 ・・・答
検証してみよう AP=3なら
3・(3+9)=36 4・(4+5)=36 でOK!
問2 下の図において、xの値を求めよ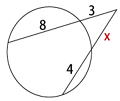 |
方べきの定理より、3・(3+8)= x(x+4)より、
x2 + 4x - 33 = 0
解の公式より、x>0だから x = -2 + √37・・・答