

3.直線の垂直条件 4.直線の方程式の新しい表現

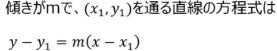
5.点と直線の距離 6.円の方程式
第3章 図形と方程式
本章では、主に以下の6つのことを学びます。
3章 1節 座標と直線の方程式 2節 円の方程式 3節 不等式の表す領域
円と直線
1.内分の公式 2.三角形の重心の座標  3.直線の垂直条件 4.直線の方程式の新しい表現  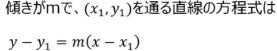 5.点と直線の距離 6.円の方程式   |
1節 座標と直線の方程式
![]()
線分の内分

上の図は線分ABを2:1に内分する点Pを表しています。
線分ABの内部にあって,AP:PB=2:1となる点」を内分点といいます
次の図は線分ABをm:nに内分する内分点Pを示しています。
![]()
「線分ABをm:nに内分する点Pとは,線分ABの内部にあって,
AP:PB=m:nとなる点」をいいます.
| 例1 線分ABを3:7に内分する点Pは 例2 |
答
例1 ![]() 点P -2
点P -2
例2 ![]() 点P 0
点P 0
問 直線上に2点A(a),B(b)があるとき、線分ABを3:2に内分する点Pの座標Xを求めてみよう。 教ⅡP41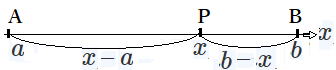 |
a<bのとき、a<x<b であるから
AP=x−a、PB=b-x
AP:PB=3:2より (x−a):(b-x)=3:2
2(x−a)=3(b-x) 整理すると
(3+2)x=2a+3b
![]() (a>bのときも同様である)
(a>bのときも同様である)
一般に次のことが成り立つ。
■内分点の座標
| 2点A(a),B(b)を結ぶ線分ABを m:nに内分する点Pの座標Xは とくに、線分ABの中点Mの座標Xは |
| 例 2点A(-2),B(6)を結ぶ線分ABを3:1に内分する点Pの座標Xは? また、中点Mの座標Xを求めてみよう。 |

![]() …答
…答
中点Mの座標Xは ![]() …答
…答
| 問1 2点A(3),B(7)を結ぶ線分ABを2:1に内分する点Pの座標は? また、中点Mの座標は?  |
解答
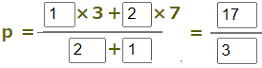 中点Mの座標は5
中点Mの座標は5
問2 2点A(-2),B(5)を結ぶ線分ABを1:3に内分する点Qの座標qは |
解答
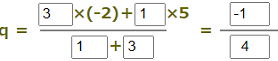 中点Mの座標は3/2
中点Mの座標は3/2
■外分点の座標
| 下の図のように線分AB上の延長上に点Pがあって AP : PB=3:1であるとき、点Pは線分ABを3:1に外分するといいます。 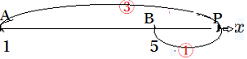 線分ABを1:3に外分する点Qは下の図のようになります。 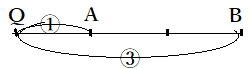 線分ABをm:nに外分する際、次のように考えると分かりやすいでしょう。
|
しっかり理解しておいてください。
|
下の図の線分ABを3:2の比に外分する点を作成してみよう。 |
■外分点の座標
2点A(a),B(b)を結ぶ線分ABをm:nに外分する点の座標Xは、内分と同様に求めると、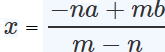 となります。 ※内分の式nに-がつきますね。 となります。 ※内分の式nに-がつきますね。 |
| 例題 2点A(1)、B(5)を結ぶ線分ABを3:1に外分する点Pの座標Xは |
答 X=(-1×1)+ (3×5) / (3-1)=7
右図参照 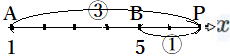
| 問1 2点A(1), B(5)を結ぶ線分ABを2:1に外分する点P、 また、1:2に外分する点Qの座標Xを求めなさい。 |
答
図を書いてもOKですが、うまくいかない場合は公式を使ったほうが早いですね。
2:1をm(2), n(1) 、2点A(1), B(5)をa(1), b(5)
公式 ![]() から
から
P={(-1)×1 + (2×5)}÷(2-1)= 9 …答
1:2をm(1), n(2) 、2点A(1), B(5)をa(1),b(5)
Q={(-2)×1 + (1×5)}÷(1-2)= -3 …答
図だったら以下の通り

![]()
2:1 1:2
| 問2 次の2点A, Bを結ぶ線分ABを2:3に外分する点Pを図示しなさい。 また3:2に外分する点Qの座標Xを求めなさい。  |
解答 Aからの距離が2で,Bからの距離が3になる点。外分する点はAの外側
m=2, n=3
P={(-3)×0 + (2×1)}÷(2-3)= -2 …答
 -2
-2
3:2に外分する点Q 3…答
☝
問3 次の2点A, Bを結ぶ線分ABを3:1に外分する点Pを図示しなさい |
まず、公式を用いましょう。
![]() m=3,n=1 a=-2,b=2
m=3,n=1 a=-2,b=2
P={(-1)×(-2) + (3×2)}÷(3-1)= 4 …答
図で考えてみましょう
線分ABを3:1に外分する点は,Bの外側にあります.
次に,外分比は比率なので,実際のAB間の距離に応じて長さを考えます.
この問題では,AB間の距離が4だから,3:1=6:2として,Aからの距離が6で,Bからの距離が2になる点になります
 4
4
☝
この問題では,AB=4だからm−n=4, m:n=3:1となるようにします
![]()
第1象限、第2象限など象限を覚えていますか。
| 例 原点O、点P(2,1)間の距離OPを求めてみよう |
答 √5
| 問1 2点A(1,2),B(4,6) 間の距離ABを求めなさい。 |
答 5
| 問2 2点A(2,3),B(5,-1) 間の距離ABを求めなさい。 また、原点O、点C(1,-4)間の距離 |
答 5 √17
■平面上の内分
■平面上の外分
■重心
| Gが重心のとき AG:GP=2:1 BP=CP |
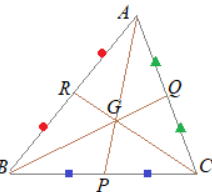 |
|
問 Gが重心のとき△BGDと△ABCの面積比を答えなさい。 |
解説 △ABDは△ABCの面積の半分 さらに重心Gは線分ADを2:1に分けるため
△ADBと△GDBの面積比は3:1になることから、△BGDと△ABCの面積比は1:6
1:6 …答
| 問 3点A(2,3),B(1、−1),C(6、1)を頂点とする△ABCの重心Gの座標を求めなさい。 |
答 G(3、1)
![]()
直線を表す式について学び、傾きや直線上の点の座標から式を求めます。
中学でも学習しましたが、ここではもっとスマートに解く方法を学びます。
yの変化量 /xの変化量 =変化の割合= 傾き
| 復習問題 次の2直線の交点の座標を求めよ。 y=2x−1, y=-x+5 |
交点の座標(2,3)
| 問1 点(2,−5)を通り、傾きが−4の直線の方程式を求めよ。 |
中学で学習したやり方
y=-4x+bとおく。
点(2,−5)を通るので、-5=-8+b b=3
よって y=-4x+3…答
今回学習するやりかた y+5=-4(xー2) y=-4x+3 答
| 問2 2点A(2,−1)とB(4,3)を通る直線の方程式を求めよ。 |
答 y+1=2(x−2) y=2x−5
| 問3 2直線 x+y−4=0 と2x−y+1=0 の交点と、点(−2,1)を通る直線の方程式を求めよ |
答 x+y−4=0…①
2x−y+1=0…② ①と②を足すとx=1,y=3 (1,3)
よって、点(1,3)と点(−2,1)を通る直線であることが分かる。
![]()
![]()
◆2直線の平行
| 問1 点(3,1)を通り、y=−2x+5に平行な直線の方程式を求めよ |
答 y−1=-2(x−3) よって y =-2x+7
| 問2 点(2,−1)を通り、x+y+3=0に平行な直線の方程式を求めよ |
答 x+y+3=0 から y=−x−3で、傾きは−1
点(2,−1)を通る直線なので、
y+1=−(x−2) から y=-x+1(答)
◆2直線の垂直
| 問1 直線 y=3x+2に垂直な直線の傾きを求めよ |
求める垂直な直線の傾きをmとおく。
3m=−1 m=−![]()
| 問2 直線 y=−2x+1に垂直な直線の傾きを求めよ |
求める垂直な直線の傾きをmとおく。
−2m=-1 m=![]()
| 問3 (1)点(3,1)を通り、直線y=-2x+5に垂直な直線の方程式を求めよ (2)点(4,1)を通り、直線y= |
(1) 求める直線の傾きをmとおく −2m=-1 m=![]()
y−1=![]() (x−3) よって、y=
(x−3) よって、y=![]() x−
x−![]()
(2) 求める直線の傾きをmとおく ![]() m=-1 m=−3
m=-1 m=−3
y−1=−3(x−4) よって、y=-3x+13
| 問4 点(4,1)を通り、直線2x+y+4=0に垂直な直線の方程式を求めよ |
y=-2x−4 求める直線の傾きをmとおく −2m=-1よって m=![]()
y−1=![]() (x−4) よって、y=
(x−4) よって、y=![]() x−1
x−1
| 問5 2直線2x+y−6=0と x−2y+2=0の方程式は垂直であることを証明せよ |
証明) 2x+y−6=0の方程式は y=−2x+6
x−2y+2=0の方程式は y=![]() x+1 で表せる。
x+1 で表せる。
このとき2直線の傾きは、 (−2)×![]() =-1
=-1
よって、この2直線は垂直である。
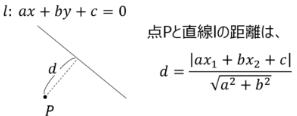
■点と直線の距離
| 例1 点(3,1) を通り、直線y=2xの最短距離を求めてみよう。 |
y=2x に直角な式はy=![]() x +bで表せる。この式は(3,1)を通るので、
x +bで表せる。この式は(3,1)を通るので、
1=![]() +b よってb=
+b よってb=![]() よって式は、y=
よって式は、y=![]() x +
x +![]()
y=2xと y=![]() x +
x +![]() の共有点は(1,2) なので、3平方の定理から 答は√5
の共有点は(1,2) なので、3平方の定理から 答は√5
※公式を使う解き方もあります。
| 問1 次の点と直線の距離を求めよ。 点(3,1)を通り、直線 3x−4y+5=0 |
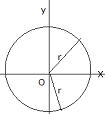 |
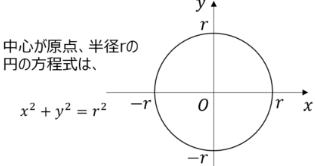
原点Oを中心とする半径rの円の方程式は 例えば半径が1のときx2+y2=1 中心はO(0,0) |
中心が(a,b)、半径rの円の方程式は、
![]() のように表します。
のように表します。
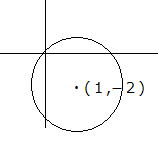 |
左図の円の中心(a,b)、半径を1としたら、円の方程式は (x-1)2+{y-(-2)}2=1 (x-1)2+(y+2)}2=1となります。 また、円の半径を3としたら、(x-1)2+(y+2)2=9 |
| 例1 方程式 (x+2)2+(y-1)2=10 が表す円の中心の座標と半径を求めよ。 |
解説
方程式(x+2)2+(y-1)2=10は
{(x−(−2)}2+(y-1)2=√10 と変形できるので、この方程式が表す
円の中心の座標は(−2,1) 半径は√10 である。
| 例2 2点A(1,2),B(5,6)を直径の両端とする円の方程式を求めよ。 |
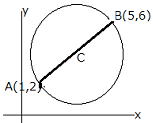 中心をCとすると、点Cは線分ABの中点であるから、
中心をCとすると、点Cは線分ABの中点であるから、
![]() ,
, ![]() よってC(3,4)
よってC(3,4)
半径はCA=![]() =√8 = 2√2
=√8 = 2√2
したがって、求める円の方程式は点(3,4)を中心とする半径 2√2 の円であるから、
(x−3)2 + (y−4)2 = (2√2)2 より (x−3)2 + (y−4)2 =8 …答
| 例3 方程式 x2+y2−2x+8y+8=0が表す円の中心の座標と半径を求めよ。 |
式を次のように変形すると、
x2−2x+y2+8y=−8
(x−1)2−1+(y+4)2−16=−8
(x−1)2+(y+4)2=9 より 中心の座標(1,−4) 半径3
| 問1 点(1,2) を中心とし、点(4,−3)を通る円の方程式を求めよ。 |
答 点(1,2) を中心とする円なので、
(x−1)2+(y−2)2= r2 点(4,−3)を通るので
9+25=r2 r2=34 なので (x−1)2+(y−2)2=34
▲ x2+y2+lx+my+n =0 式
|
例題 x2+ y2− 2x+ 8y+ 8 =0 が表する円の中心の座標と半径を求めなさい |
次のように変形しよう。
(x2−2x)+(y2+8y)= −8
(x−1)2−1+(y+4)2−16=−8
(x−1)2+(y+4)2=9 よって、中心の座標は(1,−4) 半径は3
|
問1 x2+ y2− 6x+ 4y+ 9 =0 が表する円の中心の座標と半径を求めなさい |
| 問2 3点A(2,−7), B(4,−3),C(−5,0)を通る円の方程式を求めなさい。 |
与えられた点の座標を x2+y2+lx+ my+ n =0 とおく。
点A(2,−7)を通るから、 4+ 49+2l−7m+ n = 0
2l−7m+ n=−53 …① 同様に
4l−3m+ n=−25 …②
−5l + n=−25 …③
①,②,③より l =2, m=6, n=−15
したがって、円の方程式は x2+y2+2x+6y−15 =0
| 例題1 円 x2+y2=2 と次の直線の共有点の座標を求めなさい。p60 (1) y=x (2) y=x−2 |
共有点、つまり円と直線が交わる点だから、連立方程式ですぐに導きだせるね。
| (1) x2+y2=2…① y=x …② より (1,1)と (−1,−1) 右図 |
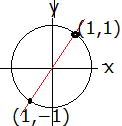 |
| (2) x2+y2=2…① y=x−2…② より (1,−1) ※円と直線y=x−2は1点で接します。 |
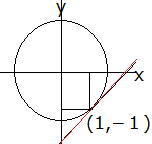 |
■共有点の個数
上の例題ではグラフから分かるように (1)は共有点が2個、(2)は1個ですね。
ここでは共有点の個数について考えてみることにする。
| 円 x2+y2=2 と直線 y=x+3の共有点の座標を求めてみよう。 |
2x2+6x+7=0 となり、![]() ルートの中は−20<0 となり
ルートの中は−20<0 となり
実数解をもたない。虚数になる。これは共有点を持たない。
つまり、2次方程式の判別式式 Dは
D=−20<0 となり実数解をもたない。
この場合、円と直線は共有点をもたない。
3節 不等式の表す領域
▲直線と領域
例 不等式y>x+2 ,y<x+2の表す領域はどうだろうか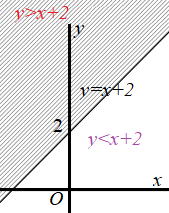 |
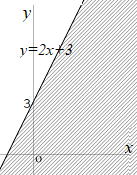
| 例 不等式 y<2x+3の表す領域はどうだろうか |
■連立不等式の表す領域
| 問1 次の連立不等式の表す領域を図示しなさい。 2x−y>1 …① x+y>2 …② |
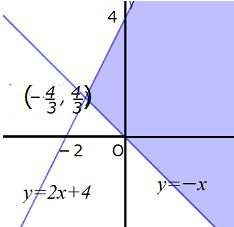
| 問2 次の連立不等式の表す領域を図示しなさい。 x+y≧0 …① 2x−y≧−4 …② |
答 y≧−x …①’
y≦2x+4 …②’ ①’,②’より
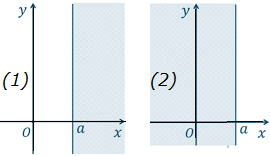
| ・y軸に平行な直線 直線l をx=aとしたとき (1) x>aのとき、領域は直線lの右側 (2) x<aのとき、領域は直線lの左側 ≧や≦のとき直線 y=aも含みます。 |
 |
| ・x軸に平行な直線の領域 直線l をy=bとしたとき (1) y>bのとき、領域は直線lの上側 (2) y>bのとき、領域は直線lの下側 ≧や≦のとき直線 y=bを含みます。 |
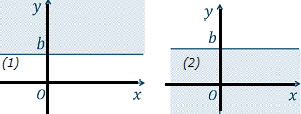 |
▲放物線と領域
放物線をy=ax2+bx+cとしたとき
y>ax2+bx+cのとき
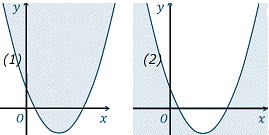
y<ax2+bx+cのとき
≧や≦のとき、放物線上の境界線を含みます。
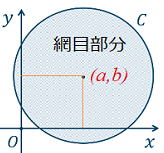
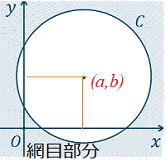
▲円と領域
| 領域 ・円の内部 x2+y2< r2 (x−a)2+(y−b)2< r2 ・円の外部 x2+y2> r2 (x−a)2+(y−b)2> r2 >,<と≦,≧。境界線を含むかどうか、 |
  |
| 問 以下のxの領域を求めなさい ① y<x2+x−2 ② y≧x2+x−2 |
① y<x2+x−2 y<(x+2)(x−1) x <−2 x > 1…答
②−2≦x≦1…答 −2と1を含む。
| 問1 不等式 x−2y−1≧0の表す領域を図示しなさい。 |
答 x−2y−1≧0を変形すると、2y≦x−1
![]()
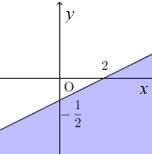
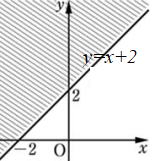
| 問2 以下の( )内に適切な式や文字を入れなさい。 (②,③は左,右,上,下のいずれか) 不等式 y>x+2の表す領域は、直線①( )の ②( 側)であり、右の図の ③( )側部分である。 |
 |
| 問3 以下の不等式の表す領域を図示しなさい。 (x−2)2+(y−3)2≦9 |
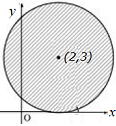 境界含む
境界含む
| 問4 以下の不等式の表す領域を図示しなさい。 ① y≦−2x+3 ② x<3 ③y≦−1 ④ x2+y2≧5 ⑤ y<−x2+2x |
答
①y≦−2x+3 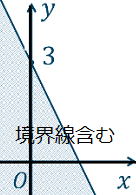 ② x<3
② x<3 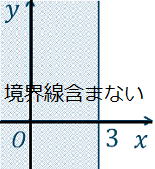
③y≦−1 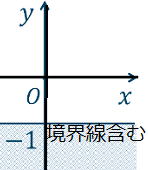 ④ x2+y2≧5
④ x2+y2≧5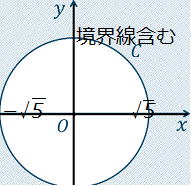
⑤ y<−x2+2x 式をグラフ用に変形しよう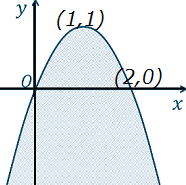
問5 下の図の斜線部分の領域を表す不等式(1), (2)を求めなさい。 (1)  境界含む (2) 境界含む (2) 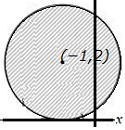 境界含まない 境界含まない |
(1) (x−2)2+(y−3)2≦9 (2)
| 問6 下の図の斜線部分の領域を表す不等式①~④を求めなさい。 ① x軸に並行でy=−1を通る直線の下側の領域を表す不等式 ② 中心は原点O(0,0)で、半径√5の円の外側の領域を表す不等式(境界含む) ③ (1,1)を頂点とし、原点O(0,0)と座標(2,0)を通る放物線の外側の領域を表す不等式 (境界含まない) ④ 座標(0,3)と座標(2,−1)を通る直線の下側の領域を表す不等式(境界含む) |
解答
① y≦−1 ② x2+y2≧5
② x2+y2≧5 
③ y<−x2+2x  ④ y≦−2x+3
④ y≦−2x+3
問7 下の図の領域を求めなさい。ただし、境界も含みます。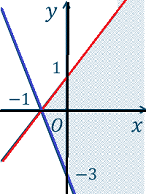 |
解説)まず、2本の直面の方程式を考えてみよう。
青の直線 座標(−1,0) と(0,−3)を通るから
赤の直線 座標(0,1) と(−1,0)を通るから
問8 下の図の領域を求めなさい。ただし、境界は含まない。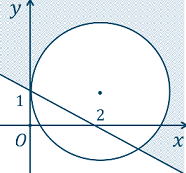 |
解説) 領域は、直線と円からなっています。
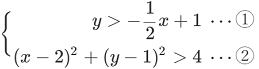 …答
…答
| 問9 中心が(1,2)で半径が4の円の内部を表す不等式を作りなさい。ただし境界線は含まない。 |
中心が(1,2)で半径が4の円は、(x−1)2+(y−2)2=16
円の内部を表す不等式だから (x−1)2+(y−2)2<16 …答
| 問10 2点A(−2,0)、B(3,0)からの距離の比が3:2である点Pの軌跡を求めなさい。 |

中心(7,0)、半径6の円
| 問11 ある点Qが放物線y=x2+1 上を動くとき点A(2,−3)と点Qを結ぶ線分の中点Pの軌跡を求めなさい。 |
