◆指数関数　指数方程式　　指数関数のグラフ
　　　　　　　　　 ◆対数関数　　　　　　　　　数学Ⅱへ戻る

　数Ⅰで学んだ以下の公式を確認しよう。

[1] a^maⁿ= a^m+ⁿ　　　[2] (a^m)ⁿ=a^mⁿ　　　[3] (ab)ⁿ=aⁿbⁿ

　　　　具体的な数値で表すと、以下のようになります。

　　　[1] a³a²= a⁵　　　[2] (a³)²=a⁶　　　[3] (ab)³=a³b³

　以下の定義をしっかり理解しよう。（重要）

　　a≠０でnが正の整数

　　　例　　　　　　　

問　　① a³×a⁴=　　　② a³×a=　　　③ (a³)³=　　　④ a³a=　　　⑤ (ab)²=

　　　⑥ (a⁴)³=　　 ⑦ (a²b)⁴=　　⑧ 3⁰= 　⑨ 2^－4　　　　⑩ 10^－2×10⁵=

　答　⑧　１　　⑨１/16　　⑩１０³＝１０００

　▲累乗根の性質

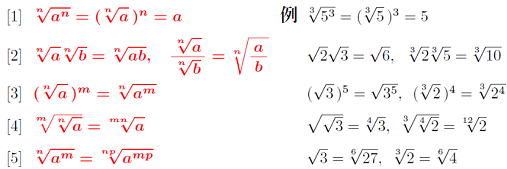
例題
　　　① ³√2×³√4＝³√8 ＝ ³√2³=2　　　② ⁴√12÷⁴√4＝⁴√3

▲有理数への拡張

（例１) ９の平方根は√9。9 = 3² であるから √9 = 3 。
（例２）１６の４乗根は「⁴√16」と書き表す。１６=２⁴ であるから ⁴√16 = 2 である。

　　
　　　　　　　　　　　　　√5=

例　

問１　(1)次の式の値を求めなさい。
　　　　　

　　　④2^－4
　　　(2)次の計算をしなさい。
　　　　　

　　　④

　答　(1)　①２　　② ０．１　　③ －３　　　　　④ 2^－4 = 1/16

　　　 (2)　①２　　② ３　　　　③ 2³√2+3³√2= 5³√2　　　　④　√2

問２　 ① (⁵√a)⁴　　　　② (⁶√4)³　　　　③ (⁴√25)²　　　　④ (⁷√a)³

答　　 ① (⁵√a)⁴＝⁵√a⁴　　　　　② (⁶√4)³＝⁶√4³＝⁶√2⁶=２
　　　③ (⁴√25)²＝⁴√25²＝⁴√５⁴=５　　　④ (⁷√a)³＝⁷√a³

▲負の整数の累乗

　　a^－n（nは正の整数）を考えてみよう。
　　上の法則が0以上の整数だけでなく負の整数でも成り立つと考えると，a ≠ ０実数）
　　　aⁿ×a^－n ＝aⁿ⁺⁽^－n)＝ a⁰ ＝１
　　　　aⁿ×a^－n ＝１… ①
　　　　　a ≠ ０であるから，この両辺①をaⁿで割ると

`a^－n`＝	１
	`aⁿ`

　「a ≠ ０ である任意の実数aについて，以下のように定義する。

`a^－n`＝	１
	`aⁿ`

　　　たとえば、
　　　　　　　

　　以下、できるだけ多くの問題に挑戦し、問題に慣れることが極めて大切です。

問１　左辺＝右辺となるよう、□の中に数値を書きなさい。

①　`a^－2`＝	１
	`a`^□

②　`a^－1`＝	１
	`a`^□

③　`a^－3`＝	１
	`a`^□

１

a⁵

=a^□

⑤　`a^－5`＝	１
	`a`^□

問２　左辺＝右辺となるよう、□の中に数値を書きなさい。

１

a²

=a^□

１

a³

=a^□

１

a⁴

=a^□

`a^－4`＝	１
	`a`^□

１

a⁰

=□

問３　以下を計算しなさい。
　①　２

＝　　　② 16

=　　　③ 27

　　④　8^{^－}

　答　　①　２＝√2　　　② ₁₆_{= (2⁴) = 8}

　　　③ 27=³√(3³) ＝3¹ =3　　　④　8^{^－} =

問４　以下を計算しなさい。
　① －3^－2　　② (－3)^－2 　　③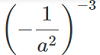

　　④

　　⑤

　　⑥ －(－a)³　　⑦

　⑧ ３a×(６ab^－²)^－1　　　⑨　６⁸÷２⁷×3^－6　　　⑩　４×１０⁸÷(２×１０⁵)

解答　６

①　－　　②　　③　＝４　　④＝２　　⑤　　　⑥　a³　
⑦　 (－１・a^－2)^－3 =　－１・a⁶ =　－a⁶　　⑧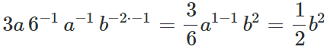　
⑨　１８　　　⑩＝２０００

問５　次の各数値を小さい順に並べなさい。

　　(1)　

　　(2) (

) 　　　(

)⁰　　　 (

)³

　　　(1)　２の累乗根で合わせましょう　＜＜＜　　

　　　(2)　 ()³　＜()⁰＜()　　　　　　　() は√５になります。

問２　次の方程式の解を求めなさい。
　　　　① 3²^x＝27^1－^x　　② 25^x＝

　　③ 8^x＝³√16　　④9^x＝⁴√27

①　②－　③　④

　　　　　
■指数方程式

例　次の方程式の解を求めてみよう
　　
　　　3²^x⁺¹＋26・3^x －9=０

　　まず3^xの形にまとめてみよう。
　　　3²^x⁺¹＝3²^x×３＝(3^x)²×３になります。☜ここがポイント

　　もとの式に戻り、
　　　3²^x⁺¹＋26・3^x －9=０　　3(3^x)²+26・3^x －9=０
　ここで3^x をtに置きかえよう。　(tでなくてもOK)
　　　3(3^x)²+26・3^x －9=０　３t² +26t－9=０
　　　　　(3t－１)(t＋９) = 0

　　　t＞０だから　t＝　　3^x＝　　より　x＝－１…答

問1　次の方程式の解を求めよ
　　
　　　2²^x⁺¹－５・2^x+2 ＋32=０

　　まず　2²^x⁺¹＝(2^x)²×２　　　　2^x+2＝(2^x)×４

　　2^{²^x⁺¹－}５・2^x+2 ＋32=(2^x)²×2－5・(2^x)×４+32
　　ここで　2^x＝a とおきましょう　　(2^x＝t でもＯＫ)

　　(2^{^x})^²×2－5・(2^{^x})×４+32=2(a)²－5・(a)×４+32

　　　=2a²－20a+32 = 2(a²－10a+16)=2(a－8)(a－2)
　　　　2(a－8)(a－2)=0 　a=2 , 8　　2^x=8 , 2^x=2より
　　　　　　　　x = 3, 1 …答

問2　次の方程式の解を求めよ
　　
　　　2²^x－５・2^x ＋4=０

　　解説
　　(2^x)²－５・2^x ＋4=０
　　2^x＝a とおくと
　　　a²－5a＋4=０　(a－4)(a－1)=0
　　　a= 4 , 1　　2^x＝4　　2^x＝1
　　　　　　　x=2, 0 　… 答

問3　次の方程式の解を求めよ
　　
　　　3^x－2・3^2－^x =７

　解説
　　　　3^2－^x = 3²×3^－^x=
　　　　
　　　両辺に3^x　を掛けると
　　　　　(3^x)²－2・3² =７×3^x
　　　　　　3^x=aとおくと　a²－18=7a
　　　　　　　　　a²－7a－18=０　(a－9)(a+2)=0
　　　　a>0 なので、a=9　　　3^x=9
　　　　　　　　　　　x=3 … 答

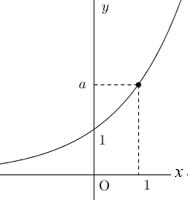
　　▲y=a^x(指数関数)のグラフ
　　　　　以下に記した指数関数のグラフの性質と、大まかな形はしっかり覚えておこう。

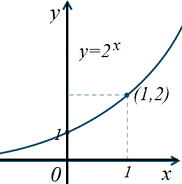
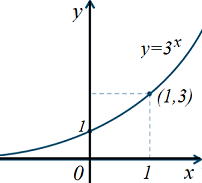
`y=a^x`　　`(a>1)`

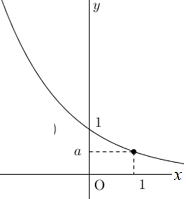
`y=a^x　(0<a<1)`

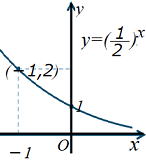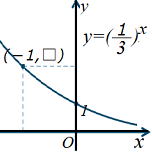y=a^x　グラフの性質グラフ図のイメージが大切
　　　　　[１]　２点(0,1),(1,a)を通る
　　　　　[２]　y＞０の範囲にある
　　　　　[３]　x軸を漸近線とする。
　　　　　[４]　a＞１のときxが増加するとyも増加する。
　　　　　　　　０＜a＜１のとき、xが増加するとyは減少する。

例題　　２⁰, ２^－1, ２

　を小さいほうから順に並べてみよう。

解説１)　グラフ　y=a^xで底aは２で１より大きいので、
　　右図より２^－1<２⁰<２

解説２)　または２⁰=1, ２^－1=

　　　　２

=√2　より答が導きだせます。

問１　次の数を小さいほうから順に並べなさい。

　　　(1)２

, ２², ２^－　　　　(2)　(

)

, （

)

, 　(

)

グラフより
　　(1)　２^－<２ <２²　　　　(2) （)< ()< () 　(>)

問２　次の値を求めなさい。
　　　(1) (⁶√25)³　　　　(2) (⁴√9)²　　(3)　(⁶√8)²

　　　　　(1)　２５＝５　　　　(2)　９＝３　　　　(3)　８＝２

問３　次の値を求めなさい。
　　　_{(1) ₆₄}　　　　₍₂₎ ₃

　　_(3)　16

　　　　(1) ４　　　　　　(2) ₃＝⁴√27　　　　　(3)　

問４　次の方程式を解きなさい。
　　　_{(1) ₂_^x_{= 16}}　　　　₍₂₎ _{₈_^x_{= 4}}　　₍₃₎_{₉_^x_{= 27}}

　　　　(1) x=4 　　　　(2) 2^3x　=2²よって　x=　　　　(3) x=

問５　次の不等式の解を求めなさい　
　　　　4^x－3・2^x +2<０

　答　左辺＝4^x－3・2^x +2＝2²^x－3・2^x +2 　
　　　2^{^x} =tとおく　t²－3t+2<0　(t－2)(t－1)<0
　　　　　グラフ(t>0)より　１＜t＜２　　2^{^x}=t　でxの関数に戻すと
　　　　　１＜2^{^x}＜２　よって　　　０＜x＜１…答　

ツール：

■対数関数　　
　　▲対数の定義：
$a^{c} = b$ $a^{c} = b$ 　　a^c=bとなるようなcのことを、log と書き、logのことを対数と言います。
　　　　　　c=log
　　　　　　たとえば 2^c=8　→ c=3
　　　　　　　　２の3乗は８ですね。指数の分野ではこの「２」を「底」といい「３」を指数といいます。
　　　　　指数部分である「3」に注目してみましょう。
　　　　　３＝□　を２と８を用いて表すと、２³=８　は　３＝log₂８　のようになります。
　　　　　　このように考えたときに導入された概念が「対数です」
　　　　　「log₂８」は「2を何乗すると8になるか」という値を表します。
　　　　　　　　　　　　log

　　　　　　　　
　　　　　最初は、なんだか難しいと思いますが、くり返し問題を解くことですぐに慣れるので、安心してください。

問　次の計算をしなさい。
　　　　① log　　② log　　　③ log　　④ log

　①　２^□＝８　　２^□(２の^□乗は)　□の中は３　よってlog

　▲対数の性質

条件　a＞０, a≠１, M>０, N>０　k:実数
　　　　　　　(1) log

　　　　　　　(2) log
　　　　　　　(3) log

　　　　　　①底がそろっているのを確認する
　　　　　　②対数の係数を真数の累乗部分にもっていく
　　　　　　③対数のたし算は真数のかけ算　対数のひき算は真数のわり算
　　　　　　④真数部分の指数を整理して計算

　例題　log
　　　　　「対数のたし算は真数のかけ算」でしたね

　　実際に計算してみましょう。

例題１　log224－log29= log224－log23= log28=3　　　　

問　(1) (2) (3)　³√2
　 (4)

(1)　５^□＝１　□の中は０　　よって　
(2) 　
(3) ２^□＝³√2＝2　　³√2
(4)

▲対数関数のグラフ

　　　以下に記した対数関数のグラフの性質と、大まかな形はしっかり覚えておこう。

x 　底が１より大きい２なので、　xが増加するとyも増加する単調増加のグラフ　　また、真数条件よりx＞０でy軸が漸近線となります。
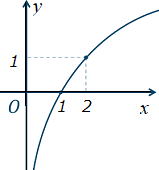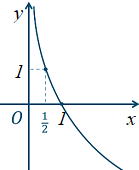
x 　　底が０＜＜１なので　xが増加するとyが減少する単調増加のグラフ　　また、真数条件よりx＞０で、同じくy軸が漸近線となります。

問　関数 xのグラフと次のグラフの位置関係を答えなさい。

　　　(1) x 　　　(2) (－x)　　　　　(3)

答　関数 xのグラフと次のグラフの位置関係。　　　(1) x 　　軸に対して対称移動したグラフ
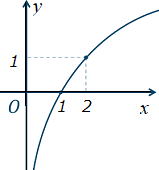関数 xのグラフと次のグラフの位置関係。　　　(2) (－x) 　　軸に対して対称移動したグラフ(に３を代入)
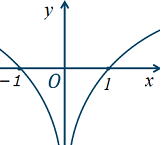関数 xのグラフと次のグラフの位置関係。　　　(3)

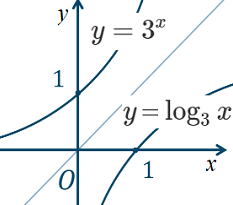▲対数関数の方程式

問　次の方程式の解を求めなさい。

　　(1)(x－1)=3　　　(2) x+(x+2)=(10－x)

　答　(1)(x－1)=3　真数条件より　x－1＞０　　x＞１　　　答　x＝9

　　　(2) 真数条件より　x＞０…① 　x＞－２…②　１０－x＞０　x＜１０…③
　　　　　①、②、③から　０＜x＜１０
　　　　　　x(x+2)=10－x 　　x²＋３x－１０＝０
　　　　　　　　(x+5)(x－2)＝０　x＝２,－５　　x＝２…答

▲常用対数

122=(1.22×100)＝0.0864+２＝2.0864
0.143=(1.43×10^－1)=0.1553－1=－0.8447

　　　100=10²=２

2³⁰は何桁の整数か。ただし２＝0.3010とする

　２＝0.3010　より　２＝10^0.3010
したがって
　　２³⁰＝(10^0.3010)³⁰=10^9.03
　　　10⁹<２³⁰<10¹⁰ となるので2³⁰は１０桁の整数である

▲整数の桁数
10¹＝10　… 2桁
10²＝100　… 3桁10³＝1000　… ４桁　　　　10ⁿ　… (n+1) 桁

ツール：