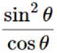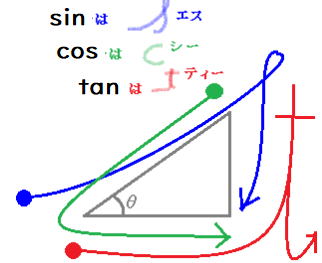
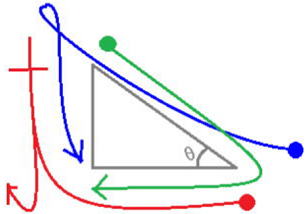
以下の表の穴埋めは、中間や期末テストに必ず出題されます。
覚えておくように指導する学校がありますが、覚えるのは大変です。
それにテストが終わってしばらくすると忘れている。
できたら、自分で考えてほしい。 表の下に考え方を説明しよう。
数学Ⅱ 戻る
1節 三角関数
一年で学習したことを復習しよう。
下図を思いだしましょう‼


以下の表の穴埋めは、中間や期末テストに必ず出題されます。
覚えておくように指導する学校がありますが、覚えるのは大変です。
それにテストが終わってしばらくすると忘れている。
できたら、自分で考えてほしい。 表の下に考え方を説明しよう。
下図の空白を埋めなさい。
| 角度(°) | 30 | 45 | 60 |
| sin | |||
| tan |
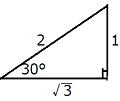
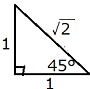
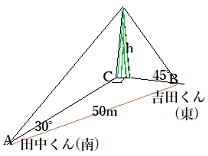
| 応用問題 田中くんと吉田くんは木の高さを測ることにした。 田中くんは真南から、吉田くんは真東から図ると、田中くんは 木の頂点の仰角は30°吉田くんは45°だった。 また、二人の離れた距離は25m, 木の高さをhメートルとして、hの値を求めなさい。 ただし、地上から目線までの高さは考慮しないこととする。 |
 |
解説
田中くんは 木の頂点の仰角は30°だから tan30°= h/AC= ![]() AC=√3 h …①
AC=√3 h …①
吉田くんは 木の頂点の仰角は45°だから tan45°= h/BC = 1 BC =h …②
また、二人の距離は50mだから、三平方の定理より、
AC2+BC2=502=2500 ①,②を代入して、3 h2+ h2=2500 h2=625
h>0 なので h=25 25m …答
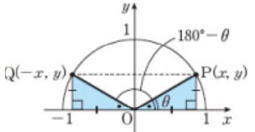
sin120°, sin135°,cos120°の値はどうだろう。
| sinθ, cosθ, tanθの値の正負はθがどの象限の角であるかによって定まり、以下に図示します。 このあと学ぶグラフと両方使うことで、問題の取り組みも楽になるでしょう。 sinθ cosθ tanθ 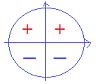 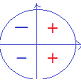 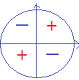 |
| 例 次の角θについてsinθ,cosθ, tanθの値を求めよう。 (1) 210° (2) -225° |
(1) 210°
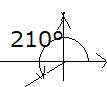 210°は(180°+ 30°)
210°は(180°+ 30°)
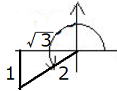
| 第3象限に30°の三角形ができます。第3象限の sin, cos,tan の正負は? |    |
sin30°、cos30°、 tan30°は
sin30°=![]() 、 cos30°=
、 cos30°=![]() 、 tan30°=
、 tan30°= ![]()
(2) -225°
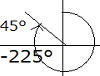 45°で考えてみよう
45°で考えてみよう
sin45°、cos45°、 tan45°は
sin45°= ![]() 、 cos45°=
、 cos45°=![]() 、 tan45°=1
、 tan45°=1
45°は第2象限なので、
sin−225°=![]() 、 cos−225°=ー
、 cos−225°=ー ![]() 、 tan−225°=-1
、 tan−225°=-1
以下のような6つの公式がありますが、三角関数は公式が多く、覚えるのも大変ですので
上の例では図で考えてみました。
![]()
0°≦θ≦90°のとき、以下の公式が成り立つ。
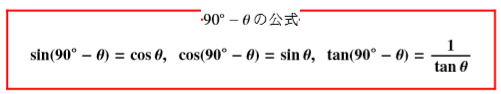
| sin(θ+180°) =-sinθ cos(θ+180°)=-cosθ tan(θ+180°) =tanθ |
sin(180°-θ)=sinθ cos(180°-θ)=-cosθ tan(180°-θ)=-tanθ |
公式を覚えるのは大変。できたら図で解決することを勧めます。
| 問 (1) sin150° (2) sin135° (3) cos150° (4) cos135° (5) sin120° (6) cos120° |
答
(1) sin150°=![]() (2) sin135°=
(2) sin135°=![]() (3) cos150°= -
(3) cos150°= -![]()
(4) cos135°= - ![]() (5) sin120°=
(5) sin120°=![]() (6) cos120°=-
(6) cos120°=-![]()
![]() 以下の公式①.②は非常に大切です。しっかり覚えておこう。
以下の公式①.②は非常に大切です。しっかり覚えておこう。
| sin2θ+cos2θ=1 ……公式① tanθ= |
| 証明にはなりませんが、公式①を実際の角度(30°)で確認してみましょう。 sinθ= sin2θ= sin2θ+cos2θ=1 になります。 同様に角度(45°)でも ( |
 |
|
問1 0°≦θ≦180°とする。 |
sin2θ+cos2θ=1 より
sin2θ=1−cos2θ sin2θ=1−![]() =
=![]()
0°≦θ≦180°で cosθ>0なので第2象限になります
sinθ>0 tanθ<0
sinθ=±![]()
0°≦θ≦180°なので sinθ=![]() …答
…答
tanθ=![]() より
より ![]() ÷
÷![]() =√3 …答
=√3 …答
| 問 0°≦θ≦180°で、tanθ=-2の時、次の各式の値を求めよ (1)tan²θ (2)1/cos²θ (3)cosθ (4)sinθ |
1) tan²θ=(-2)²=4 (2)公式 1+tan²θ=1/cos²θより 1/cos²θ=1+(-2)²=5
(3)cos²θ=1/5 0°≦θ≦180°で、tanθ=マイナスだからθは第2象限
cosθ=-1/√5
(4)sinθ=tanθ×cosθ=2/√5
|
問2 0°≦θ≦180°とする。 |
0°≦θ≦180°で cosθ>0なので第2象限になります。sinθ>0 tanθ<0
sin2θ+cos2θ=1 より
sin2θ=1−![]() sinθ=±
sinθ=±![]()
0°≦θ≦180°なので sinθ= ![]() …答
…答
公式 tanθ=![]() より
より ![]() ÷
÷![]() =-1 …答
=-1 …答
| 問3 0°≦θ≦180°とする。 cosθ= |
解説 0°≦θ≦180°でcosθ>0 だから第1象限になります。
sinθtanθ=sinθ×![]() =
= 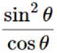
sin2θ+cos2θ=1 cosθ= ![]() を代入
を代入
sin2θ=1−![]() =
=![]() よって sinθtanθ=
よって sinθtanθ= 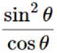
sinθtanθ=![]() ÷
÷![]() =
= ![]() …答
…答
| 問4 角度θが鋭角で、cosθ= |
sin2θ+cos2θ=1 より 第1象限
sin2θ=1−cos2θ=1−(![]() )
)
sinθ= ±![]() Aは鋭角だからsinθ=
Aは鋭角だからsinθ= ![]() …答
…答
tanθ=![]() より tanθ=
より tanθ=![]() ÷
÷![]() =
=![]() …答
…答
| 問5 θが第3象限の角で、cosθ=-3/5のとき、sinθとtanθの値を求めなさい。 |
sin2θ+cos2θ=1 より 第3象限の角だから sinθ<0 tanθ>0
sin2θ=1−cos2θ=1−(9/25)=16/25
(θが第3象限の角なので sinθ<0)
よって sinθ=-4/5 tanθ=![]() =4/3
=4/3
| 問6 0°≦θ≦180°とする。 cosθ=- |
| 解説 右図参照 0°≦θ≦180°でcosθ<0なので、第2象限になります。よってsinθ>0, tanθ<0 三平方の定理より12+y2= 32 y=2√2 図より sinθ=2√2/3 tanθ= -2√2 |
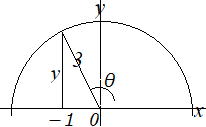 |
別解
sin2θ+(1/9)=1 sin2θ=8/9
sinθ>0なので sinθ=2√2/3
| 問7 sinθ+cosθ= |
(x+y)2=x2+2xy+y2を利用しよう。
問いの sinθ+cosθ=![]() の両辺を2乗します。
の両辺を2乗します。
(sinθ+cosθ)2= (![]() )2
)2
sin2θ+2sinθcosθ+cos2θ=1/4
公式 sin2θ+cos2θ=1を使って
2sinθcosθ=(1/4−1)=-(3/4)
sinθcosθ=-(3/8)
| 問8 θが第4象限の角で、tanθ=-2のとき、sinθとcosθの値を求めなさい。 |
第4象限の角だからsinθ<0 , cosθ>0
公式をすべて使ってもいいですが、全部覚えるのは大変。そこで、
公式 tanθ=![]() より,両辺を2乗して、
より,両辺を2乗して、
tan2θ=sin2θ/cos2θ (-2)2=(1-cos2θ) / cos2θ
4=(1-cos2θ) / cos2θ 1-cos2θ=4cos2θ
5cos2θ=1 第4象限だから cosθ=1/√5 cosθ=√5/5
tanθ=![]() より
より
sinθ=tanθ×cosθ=(-2)×(1/√5)=-2√5/5
絵をかいて三平方の定理を使ってもいいね。
| 問9 0°≦θ≦180°のとき、sinθ= |
sinθ=![]() だから1象限と2象限、 まずθ=30°
だから1象限と2象限、 まずθ=30°
0°≦θ≦180° なので、上の図からθ=150°も
答 θ=30°,150°…答
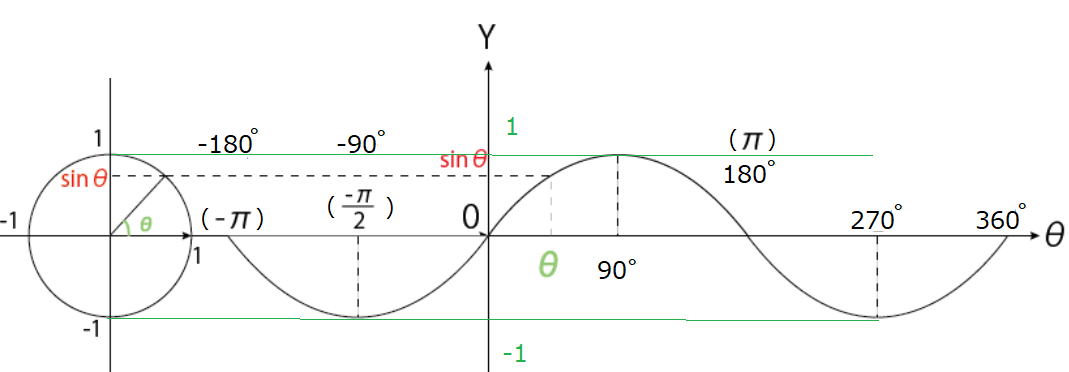
■三角関数のグラフ
sinθ、cosθ、tanθのグラフは以下のようになります。
※ 180°=πラジアン(弧度法) 360°=2π ラジアン
y = sinθのグラフ (θは角度)
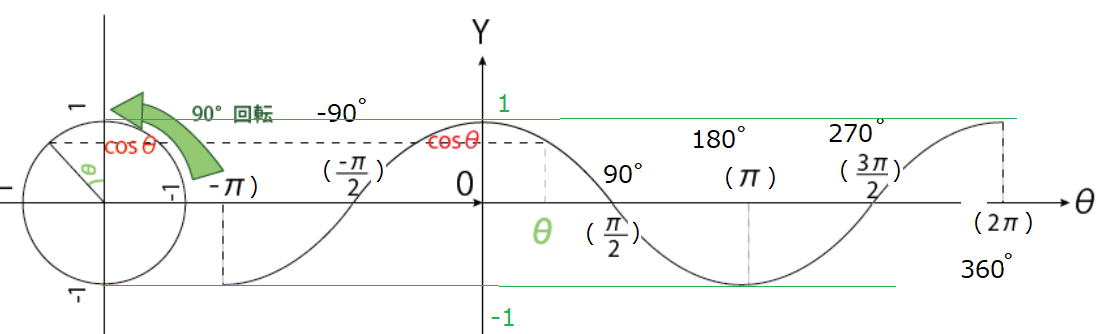
y = cosθのグラフ (θは角度)
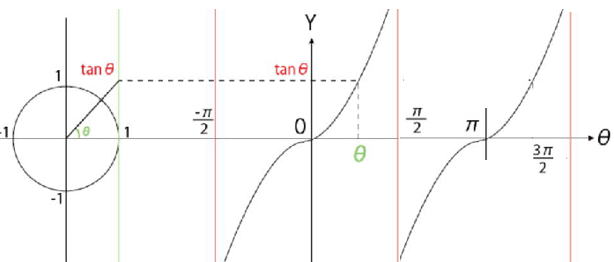
y = tanθのグラフ
(θの値が90°に近づくと、直線θ=90°に限りなく近づいていく。
このとき、θ=90°をグラフの漸近線(ぜんきんせん)といいます。
3つのグラフは手書きで簡単に描けるようになりましょう。
下図の空白を埋めなさい。
| 角度(°) | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 |
| sin | |||||||||
| tan |
| 角度(°) | 180 | 210 | 225 | 240 | 270 | 300 | 315 | 330 | 360 |
| sin | |||||||||
| tan |
答
| 角度(°) | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 |
| sin | 0 | 1 | 0 | ||||||
| 1 | 0 | - |
- |
- |
-1 | ||||
| tan | 0 | 1 | √3 | - | -√3 | -1 | - |
0 |
| 角度(°) | 180 | 210 | 225 | 240 | 270 | 300 | 315 | 330 | 360 |
| sin | 0 | - |
- |
- |
-1 | - |
- |
- |
0 |
| -1 | - |
- |
- |
0 | 1 | ||||
| tan | 0 | 1 | √3 | - | -√3 | -1 | - |
0 |
225° = 180° + 45° だから、
sin225°= sin(180°+ 45°) で考える。
よって、sin225° = -![]()
▲弧度法を使って弧の長さl や 面積sを求めてみよう。
弧度法 180°=πラジアン
弧の長さの比と中心角の比は等しいので、次の式が成り立つ。
l : 2πr = θ: 2π (左辺:弧の長さ比 右辺:角度の比)
よって 2πl=2πrθ l=rθ
面積の比と中心角の比は等しいので、次の式が成り立つ。
S :πr2 = θ : 2π 2πS=πr2θ S=![]() r2θ
r2θ
2/8
| 問 半径8㎝、中心角 ① 弧の長さl は ② 面積S は |
円周:2πr 面積:πr2
① 6π㎝ ② 24π㎠
2πr : l = 2π : ![]() π
π
円周の長さ比 中心角(ラジアン)の比
| 解説 仮に半径6㎝、角度45°を考えてみましょう。 まず、円全体の弧の長さ、面積は 円全体 弧の長さ:12π㎝だから 12π÷8=3/4π㎝ 面積:36π㎤ だから 36π÷8=9/2π㎤ |
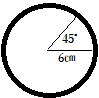 |
| 問2 半径6, 中心角 2/3πの扇形の弧の長さと面積を求めよ。 |
・扇形の弧の長さをlとする
全体の弧の長さ 2π×6 : l = 2π:2/3π
4π(答)
・扇形の面積(Sとする)
全体の面積 π×36 :S=2π:2/3π
S=12π・・・(答)
正弦定理 1年の復習
![]()
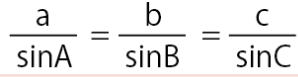
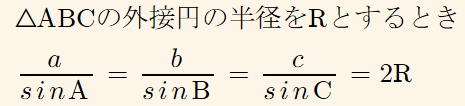
以下に説明します。
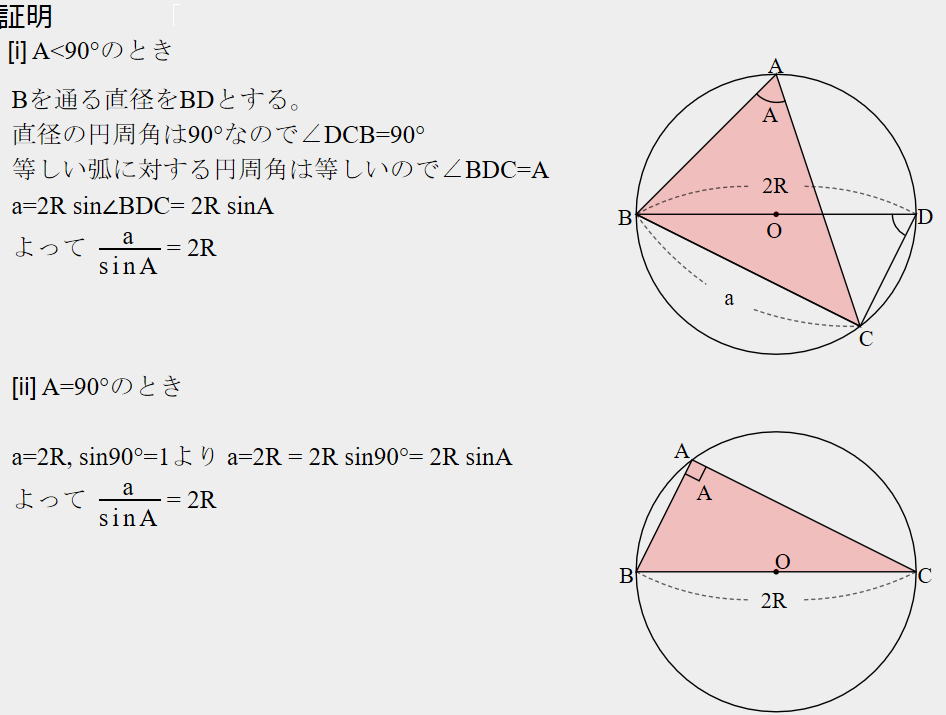
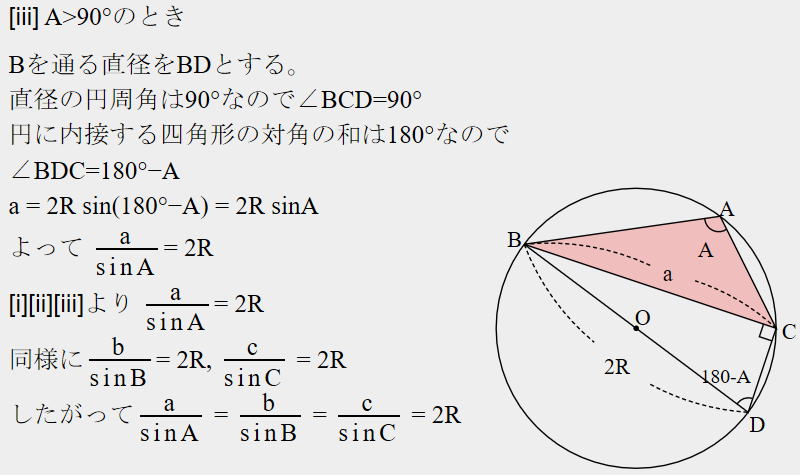
| 問1 三角形ABCにおいて、AB=4、A=75°、B=60°のとき、 辺ACの長さ、および外接円の半径を求めなさい。 |
まず、図形を簡単に書いてみよう。
| ACの長さ=b とおく 公式から bsin45°=4sin60°(sin45= また、外接円の半径は |
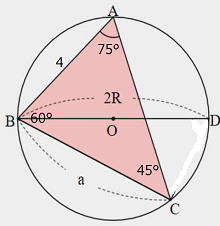 |
| 問 a=6,A=30°,B=45°のとき,外接円の半径Rとbを求めなさい。 |
解答 簡単に絵を描き,与えられたデータを図に書きこもう。
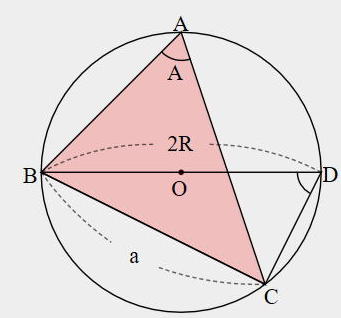
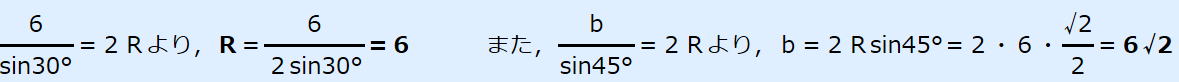 R=6,b=6√2
R=6,b=6√2
▲余弦定理


| 例 △ABCにおいて、AB=√13、AC= 3、C=60°のとき、辺BCの長さを求めてみよう。 |
角度や長さを多少、気使いながらまず簡単な図を書きましょう。
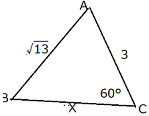 |
角度が1つ、辺の長さが2つ分かっているので余弦定理を使います。 ( 13=9+x2-6x・ x2-3x-4=0 乗法の公式を使って (x+1)(xー4)=0 x>0 なので x=4 |
問1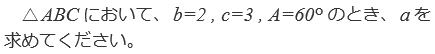 簡単な図を書こう。正弦定理を使おうとしても、aの値が未知なので、 余弦定理を用います。 2/10 問2 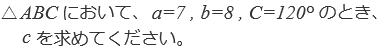 |

問3 問4 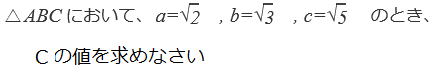 |
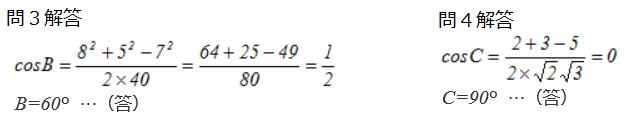
▲円の接線と弦の作る角
円の弦と、その弦の一端を通る接線のつくる角は、
その角の内部にある弧の円周角と等しい(接弦定理)
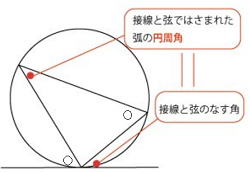
問 角度A=90°∠x の大きさを求めよ。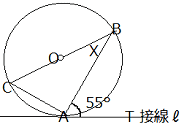 |
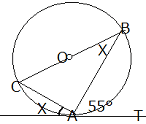
答
∠X=180°- (90°+ 55°) = 35°
方べきの定理
| 円の2つの弦AB,CDの交点(図1)、または、それらの延長の交点(図2)をPとすると、 PA×PB=PC×PD が成り立ちます。 図1 図2 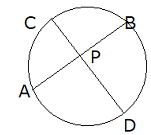 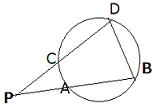 このことは円と直線の交点に作られる2組の三角形が、それぞれ相似であることから証明できます。 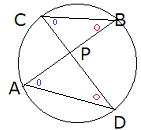 図3 図3どちらも弧AC、BDの円周角で∠A=∠C、∠B=∠Dから相似 |
問1 下の図において、PC=4, CD=5,AB=9のときPAの値を求めよ。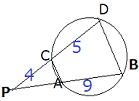 x x |
PA = x とおく。
方べきの定理より、4・(4+5)= x・(x+9)より、
x2 + 9x = 36 x2 + 9x -36 = 0
乗法の公式より、(x -3)(x+12)
x>0だから x = 3 ・・・答
検証してみよう AP=3なら
3・(3+9)=36 4・(4+5)=36 でOK!
問2 下の図において、xの値を求めよ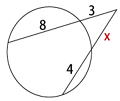 |
方べきの定理より、3・(3+8)=x(x+4)より、
x2 + 4x – 33 = 0 x=-2±√37
解の公式より、x>0だから x = -2 + √37・・・答
三角形の面積を求める
△ABCの2組の辺とその間の角度が分かれば三角形の面積が求められます。
公式は1つ覚えれば十分です
![]()
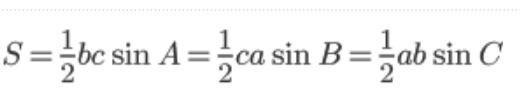
以下の証明では、角度Bが分かっているときを例にとります。

▲加法定理
sin,cosの加法定理 ![]()
sin(α+β)=sinαcosβ+cosαsinβ
sin(α−β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ−sinαsinβ
cos(α−β)=cosαcosβ+sinαsinβ
| 例 sin15°の値を求めてみよう |
sin15°= sin(60°−45°)
(sin60°×cos45°)-(cos60°×sin45°)
=(√6-√2)/4 …答
別解
sin(45°−30°) = sin45°×cos30°−cos45°×sin30°
| 問 以下の値を求めよ。 ① sin75° ② cos75° ③ cos |
答 ①(√6+√2)/4 ②(√6-√2)/4
③ cos15°=cos(45−30)=cos45cos30+sin45sin30= (√2+√6)/4
④ sin![]() π=sin165°=sin(120+45)=sin120cos45+cos120sin45=(√2-√6)/4
π=sin165°=sin(120+45)=sin120cos45+cos120sin45=(√2-√6)/4
▲2倍角の公式 ![]()
| sin2α=2sinαcosα cos2α=cos2α-sin2α=1-2sin2α=2cos2α-1 tan2α=2tanα/(1-tan2α) |
公式をすべて覚えなくても、以下、加法定理や他の公式から導きだせます。
| 問 上の公式 sin2α=2sinαcosα を加法定理を使って証明しなさい |
証明 sin2α=sin(α+α)=sinαcosα+cosαsinα=2sinαcosα
| 問 cos2α=cos2α-sin2αを加法定理を使って証明しなさい |
証明 cos2α=cos(α+α)=cosαcosα-sinαsinα=cos2α-sin2α
| 問 cos2α-sin2α=1-2sin2αになるのを証明しなさい |
sin2α+cos2α=1より cos2α=1-sin2α
左辺 cos2α-sin2α=(1-sin2α)-sin2α=1-2sin2α
| 問 cos2α-sin2α=2cos2α-1になるのを証明しなさい |
sin2α+cos2α=1より sin2α=1-cos2α
左辺 cos2α-sin2α=cos2α-(1-cos2α)=2cos2α-1
▲三角関数の合成の応用
| 例 y=sinθ+√3cosθの最大値、最小値を求めてみよう。 |
y=sinθ+√3cosθ=2(![]() sinθ+
sinθ+![]() cosθ)
cosθ)
![]() =cos
=cos![]()
![]() =sin
=sin![]() より √4=2
より √4=2
2(![]() sinθ+
sinθ+![]() cosθ)=2(sinθcos
cosθ)=2(sinθcos![]() +cosθsin
+cosθsin![]() )
)
=2sin(θ+![]() ) y=2sin(θ+
) y=2sin(θ+![]() )
)
-1≦sin(θ+![]() )≦1 だから の最大値は2 最小値は-2
)≦1 だから の最大値は2 最小値は-2
| 問1 0≦θ≦2πのとき √3sinθ-cosθ=1を解きなさい。 |
√3sinθ-cosθ=1 左辺を合成すると、
√3sinθ-cosθ=2(![]() sinθ-
sinθ-![]() cosθ)
cosθ) ![]() =cos ,
=cos ,![]() =sin だから
=sin だから
=2(sinθ-![]() ) よって 2(sinθ-
) よって 2(sinθ-![]() )=1 sinθ-
)=1 sinθ-![]() =
=![]()
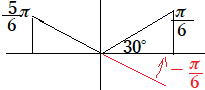
0≦θ≦2πより,-![]() ≦θ-
≦θ-![]() <
< ![]() (右図)
(右図)
![]() でプラスなので1,2象限となり θ=
でプラスなので1,2象限となり θ=![]() ,π …答
,π …答
| 問 関数 y=cos2θ-2sinθ+2 (0≦θ<2π)の最大値・最小値、およびそのときのθの値を求めなさい。 |
|
2倍角の公式を使う解き方 y=cos2θ-2sinθ+2 0≦θ<2π 2倍角の公式から |
2倍角の公式を使わない解き方 |
ツール
:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()