微分・積分 [数Ⅱ目次] に戻る
1節 微分係数と導関数
2節 関数の値の変化
3節 積分法
■微分・積分って、なーに?
※グリーンで記述した個所は物理で学習するので、あくまで参考にしてください。
距離を時間で限りなく0に近づける(微分する)と速度、
s=v×t s:距離 v: t:時間
s'=v (参考)
速度を時間で限りなく0に近づけると加速度になります。
・速度と時間に関する公式
v=v₀+at (参考)
v:加速した後の速度 v₀:加速する前の速度(初速)
a:加速度(単位はm/s²) t:時間(単位は秒)
・距離と時間に関する公式)
x=v₀t+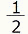 at2 at2
x:距離 v₀:加速する前の速度(初速)
a:加速度(単位 m/s²) t:時間(単位 秒)
反対に、加速度を時間で積分すると速度、速度を時間で積分すると距離になります。
微分と積分はそれぞれ逆の操作になっていて、微分と積分の関係でつながっています。この「時間」の部分を限りなくゼロに近づけた状態まで取り扱うのが微分と積分です。
他に球の体積V=4/3πr3を半径rで微分すると V’=4πr2で、
同じ半径の面積の円が4つできますし、
さらに、面積S=πr2 を半径rで微分すると、その円の円周の長さ(2πr)になります。
微積分は日常の生活の中で、各分野で使われています。
|
それでは微分から学習していきましょう。
まず、関数を表す記号から覚えましょう。
y = 2x+1やy = x2 のようにy がxの関数であることを、
y =f (x) のように表します。
関数 y =f(x)において、 f(x)の式に x = aを代入して
得られるyの値を y = f (a) で表します。
分かりにくいので実際に例題をやってみましょう。
例 関数 f (x) =x2+2xにおいて、f(3)のとき、
f(3) = 32+2×3 =15になります。
f(−1) = (-1)2+2×(-1) = -1 です。
問 関数f (x) = x2-3xにおいて、次の値を求めなさい。
(1) f(1) (2) f(2) (3) f(-1) (4) f (-2) |
■平均変化率
一般に,関数 y=f(x)において、xの値がaからbまで変化するとき
xの変化量は b−a
yの変化量は f(b)−f(a)である。
このとき
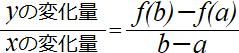 を、xの値がaからbまで変化するときの平均変化率という。 を、xの値がaからbまで変化するときの平均変化率という。
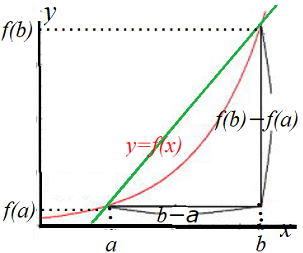
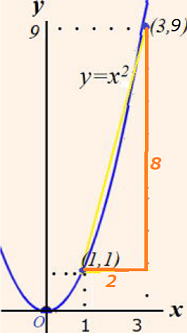
この値は曲線 y=f(x)上の2点
(a , f(a)), (b , f(b))を通る直線の傾きに等しい。(右図) |
 |
 |
例題
関数 f(x)=x2 において、xの値が1から3まで変化するときの平均変化率を求めてみよう
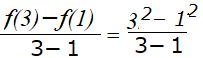 =4 =4
それでは、以下の問いに答えなさい。
問 関数 f(x) = 2x2−3について以下の問いに答えよ。
(1) x=2 から x=4 まで変化するときの平均変化率を求めなさい。
(2) x=2から x=2+h まで変化するときの平均変化率を求めなさい。 |
|
 |
答
(1) 関数 f(x) = 2x2−3
x=2から x=4 まで変化するときの平均変化率を求めなさい
x=2のとき
f(2) = 2・22−3= 5
x=4のとき
f(4) = 2・42−3= 29 表にすると、
平均変化率は 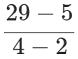 =12…答
=12…答
(2)関数 f(x) = 2x2−3
x=2から x=2+h までの平均変化率を求めなさい。
x=2のとき
f (2)=2・22−3= 5
x=2+hのとき
f (2+h)= 2・(2+h)2−3 =
8+8h+2h2−3 = 2h2+8h+5
平均変化率は 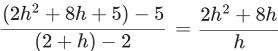 =2h+8…答
=2h+8…答
問3
(1) 関数 f(x) =2 x2−1について x=2から x=1+hまで変化するとき、平均変化率を求めなさい。
(2) 関数 f(x) = x2+3x について2から2+hまでの平均変化率を求めなさい。
|
答
(1) x の変化量 h−1
y の変化量
x =2のとき 7
x =1+hのとき f(1+h)=2(1+h)2−1
平均変化率は 2(1+h)2−1−7/(h−1)
2h2+4h−6/(h−1) 2(h2+2h−3)=2(h+3)(h−1)
よって、2(h+3) …答
(2) 7+h …答
■微分係数
例1
(1) 関数 f (x) =x2 について 、x=1における微分係数を求めてみよう
x=1における微分係数 f' (1)は
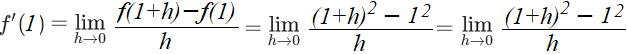
=2…答
(2) 今度は、関数 f (x) =x2 について、 x=aにおける微分係数を求めてみよう。
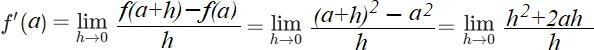
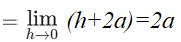 2a …答 2a …答
|

|
| 問1 関数 f (x) =2x2−3 の x=2における微分係数を定義に従って求めなさい。 |
解説 f (x) =2x2−3
まずx=2からx=2+hにまでの平均変化率を考えましょう。
x=2のとき
f(2)=8−3=5
x=2+hのとき
f(2+h)=2(2+h)2−3=2h2+8h+5
x=2 →2+h
f(x)=5 → 2h2+8h+5より
平均変化率は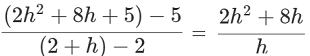 =2h+8
=2h+8
よって、微分係数f'(2)はh→0に近づけたときとなるため、
f'(2) =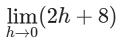 =8 よって f(x)'=8…答
=8 よって f(x)'=8…答
|
問2 微分係数の定義にしたがって,次の関数のx=−1における微分係数を求めてみよう
f (x) =−x2+3x−5 (x=−1)
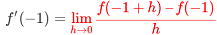
・f '(−1+h)=−(−1+h)2+3(−1+h)−5 =−h2+5h−9
・f '(−1)= 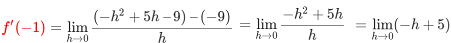
= 5…答
|
| 例 同じ問題 f (x)=−x2+3x−5の微分係数を、より簡単なやり方で求めてみよう |
f (x)=−x2+3x−5 (x=−1)
微分すると f '(x)=−2x+3
したがって、x=−1における微分係数 f '(−1)は
f '(−1)=−2×(−1)+3=5 …答
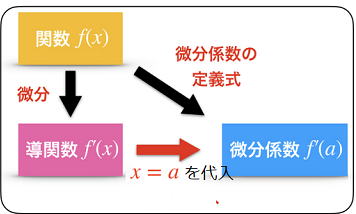
微分係数と導関数の違い
・微分係数 f '(a)は定数で、関数 y=f(x) 上の特定の点(x=aの接点)における接線の傾きです。
・導関数 f '(x)は関数で、関数 y=f(x) 上のすべての点における接線の傾きをxの関数で表したものです。
つまり、x=aにおける微分係数を求めるときは、f(x) を微分して、それにx=aを代入します。
|
 |
関数 f (x) =x2 の導関数 f '(x)は次の式で定義されます。
関数 f(x)の導関数 f '(x)は
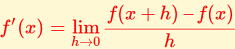 で表せます。
で表せます。
上の導関数の定義の式においてhはxの変化量を表し,f (x+h)−f (x)は
それにともなう変化量を表しています。
これらをそれぞれxの増分, yの増分といい,それぞれ△x,△yで表します。
(△:デルタ)
△x,△yを用いると
f (x)の導関数 f '(x)は
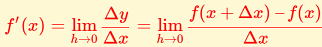 と表せます。また、
と表せます。また、
f '(x)の他にy',や
△x, △y を用いて 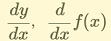 なども用いられます。
なども用いられます。
それでは、導関数の定義にしたがい、次の関数を微分してみよう。
① f (x)=2x+5 ② f (x)=−x3 |
答
① f(x)=2x+5
f '(x)=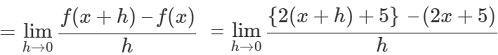
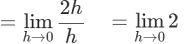 =2…答
=2…答
② f (x)=−x3
f '(x)=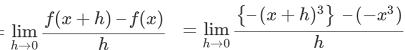
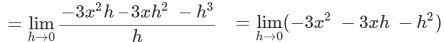 = −3x2…答
= −3x2…答
| ■xnの微分 |
| n=1, 2, 3, 4……のとき、 (xn)' = nxn-1 |
公式としてはとても重要ですが、具体的な数で微分するのに慣れたあとで再度、
微分する際、どこの数値がどのように変わっているかを見てください。
実際の数値でやってみましょう。
例 以下の関数を微分してみましょう。
(1) y=x2 → y'=2x
(2) y=x2+2x → y'=2x+2
(3) y=x3 → y'=3x2
(4) y=x3+2x2 → y'=3x2+4x
(5) y=x4+x3+2x2+2x+3 → y'=4x3+3x2+4x+2
指数が前の係数となり(実際は指数×係数で x2や x3 は指数が1なので、そのまま指数が係数になったようにみえます。
(x2は1x2、x3は1x3ですね。1は省略) それに、指数−1になっています。 |
問 以下の関数を微分しなさい
(1) y=2x2−5x-1 (2) y=x3+3x2-1
(3) y= −2x3+9x2-12x+5 (4) y=x3−6x2+9x |
答
(1) y=2x2−5x-1 → y' =4x−5
(2) y=x3+3x2-1 → y' =3x2+6x
(3) y=−2x3+9x2-12x+5 → y' =−6x2+18x-12
(4) y=x3−6x2+9x → y'=3x2−12x + 9
さらに、微分は接線の傾きを求めるための計算でもあります。
微分係数と接線の傾きと接線の方程式
曲線 f (x)上の点(a , f (a))における接線の傾きは微分係数 f' (a)に等しい。
|
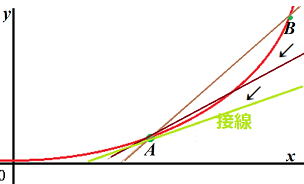
f ' (x)はその点における傾きであることを、以下のグラフで考えてみましょう。
接線の方程式
関数 y = f (x) のグラフ上の点 (a , f(a)) における接線の方程式は y−f (a) = f ' (a) (x−a) に等しい。
微分係数が曲線 y = f (x) 上の点 (a , f(a)) における接線の傾きであることを以下のグラフで確認しよう。
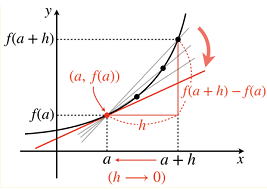
h → 0: 増加hを限りなく0に近づけていく。下に lim (リミット)を使った公式を書いています。
参考まで) 同じことを符合を変えて再度説明しましょう。
微分係数 f '(x) = は,曲線y= f '(x) 上の点(x, f '(x) における接線の傾きを表す。
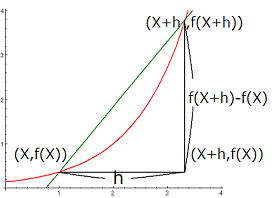
図からXの増加量がhのとき、yの増加量はf (x+h)-f '(x)となります。このhを限りなく0に近づけていくことにより、傾きを求めることができます。
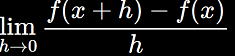
|
例 曲線 y = x2 上の点(1,1)における接線の傾きはどうなるだろうか
|
f (x) = x2 とおくと f ' (x) = 2x
x=1 f'(1) = 2 接線の傾きは2になります。
次の極限値を求めてみよう。
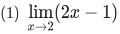 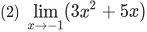 |
答 (1) 3 (2) −2
問1 曲線 y = x2 上の点(3,9)における接線の方程式を求めよ。
|
f(x) = x2 とおくと f' (x) = 2x
x=3 f'(3) = 6 接線の傾きは6
y = x2 上の点(3,9)における接線の方程式は
y-9 = 6(x-3)
したがって、y-9 = 6x-18 y-9 = 6(x-3) y = 6x-9…答
問2 関数 y = 2x2 -5x-1のグラフについて、
(1) 点(2,−3)における接線の方程式を求めよ。
(2) 傾きが−1のときの接線の方程式を求めよ。
(3) 傾きが3のときの接線の方程式を求めよ。
|
(1) f (x) =2x2 -5x-1 とおくと、 f ' (x) = 4x-5
f ' (2) = 4×2-5 = 3 … 接線の傾き
y = 2x2 -5x-1 上の点(2,⊸3)における接線の方程式は
y+3=3(x-2) y = 3x-9 答
(2) f (x) =2x2 -5x-1 とおくと、 f ' (x) = 4x-5
傾きが−1だから 4x-5= -1 4x=4 x=1
x=1のとき y=-4 (1,−4)における接線の方程式だから
y+4 = -1(x-1) y = −x-3 答
(3) f ' (x) = 4x-5より傾きが3だから,
4x-5=3 x=2 傾きが3の座標(2,-3)
y+3 = 3(x-2) y = 3x-9 答
| 問3 関数 y=x2−4x+1 のグラフ上の点 (3,−2) における接線の方程式を求めよ。 |
f (x) =x2−4x+1 とおく。 f ' (x) = 2x-4
f ' (3) = 6-4 = 2 … 接線の傾き
y=x2−4x+1 上の点(3,−2)における接線の方程式は
y−(−2)=2(x-3) y +2 = 2x-6 y = 2x-8
|
問4 次の接線の方程式を求めよ。
(1) y= x2−4x 上の点 (1,−3)における接線の方程式
(2) y= x3−2x2+5x+1上の点 (2,11) における接線の方程式
|
答 (1) y=−2x−1 (2) y=9x−7
|
問5 次の接線の方程式を求めよ。
(1) y= x2−2x+3上の接線で、点(−1,−3)を通る接線。
(2) y= −x2+4x−3の接線で、傾きが6となる接線。
|
答 (1) y=2x−1 y=−10x−13 (2) y=6x−2
|
問6 関数 y=2x2+3x−4のグラフ上に点A(1,1)をとる。
(1) 点Aにおける接線lの傾きmを求めよ。
(2) 点Aにおける接線lの方程式を求めよ。
|
答 (1) m=7 (2) y=7x−6
■関数の極大・極小
極限値
<極値の定義>
関数f (x)において,
1.f ' (x) の符号が,x=aの前後で,正から負に変わるとき,
f (x) は x=aで極大になるといい, f(a) を極大値という。
2.f ' (x) の符号が,x=aの前後で,負から正に変わるとき,
f (x) はx=aで極小になるといい, f(a)を極小値という。
極大値と極小値をまとめて極値という。
|
f ´ (x)はその点における傾きでしたね。再度、以下のグラフで考えてみましょう。
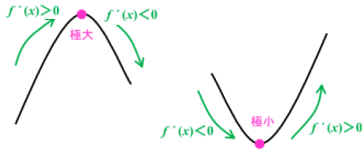
これより,f ´ (x) の符号が正から負,または負から正というように変化するとき,
極値をもつことがわかります。
3次関数 y = ax3 のグラフは概ね以下のような曲線を描きます。
a>0のとき a<0のとき

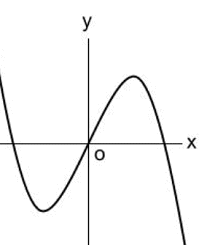
例 関数 y=x3−3x2+2 の極値を求めてみよう。
a>0 傾きが変化する点(座標)を求めてみよう。
それには、まず微分する。 y' = 3x2−6x = 3x(x−2)
傾きがプラスからマイナス、マイナスからプラスに変化する点
y´=0は x=0 ,2
x=0のとき極大になり、極大値は2
x=2のとき極小になり、極小値は−2
y=x3−3x2+2 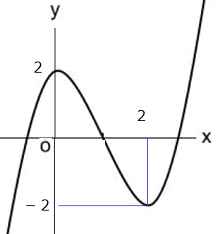
問1 次の関数の極値を求めなさい。
(1) y = -2x2+4x (2) y = x3+3x2 −1
(3) y= −2x3+9x2−12x+5 |
解答
(1)x=1のとき 極大値2
(2)傾きが変化する点を求めましょう。
微分します。 y'=3x2+6x = 3x(x+2)
傾きがプラスからマイナス、マイナスからプラスに変化する点
y'=0は x =0と,−2
y= f (x) = x3+3 x2−1
f (−2)=−8+12−1=3 f (0)=−1 グラフ①より
x= −2のとき極大になり、極大値は3
x =0のとき極小になり、極小値は−1 |
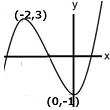 |
(2) y = −2x3+9x2−12x+5
微分 y´=−6x2+18x−12 =-6(x2−3x+2)=-6(x-2)(x-1)
傾きがプラスからマイナス、マイナスからプラスに変化する点
y´=0は x=1と,2
増減表
| x |
… |
1 |
… |
2 |
… |
| y' |
- |
0 |
+ |
0 |
- |
| y |
⤵ |
0 |
⤴ |
1 |
⤵ |
|
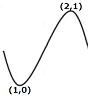 |
y=f (x) = −2x3+9x2−12x+5 f(1) =0 f(2) =1上のグラフ②より
x= 1のとき極小になり、極小値は0
x= 2のとき極大になり、極大値は1
問2 次の関数の増減表とグラフを書きなさい。
y = x³−6x²+9x |
答
y=x³−6x²+9x y’=3x2−12x+9
=3(x2−4x+3)=3(x−1)(x−3)
以上からyの増減表は
| x |
… |
1 |
… |
3 |
… |
|
y' |
+ |
0 |
− |
0 |
+ |
|
y |
⤴ |
4 |
⤵ |
0 |
⤴ |
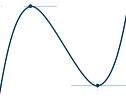
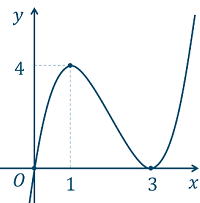
x=1のとき極大値4
x=3のとき極小値0
|
a>0のときは
 |
| 問 関数 y = x3-3x2+1(-2≦x≦3)の最大値、最小値を求めなさい。 |
y’=3x²−6x =3x(x -2)
| 増減表 |
-2 |
… |
0 |
… |
2 |
… |
3 |
| y' |
|
+ |
0 |
- |
0 |
+ |
|
| y |
-19 |
⤴ |
極大
1 |
⤵ |
極小
-3 |
⤴ |
1 |
x=0,3のとき 最大値 1
x =-2 のとき 最小値 -19
問 関数 f(x) =-2x3+3ax2+bが x=1において極大値5をとるような定数a,bの値を求めよ。
また、そのときのf(x)の極小値を求めよ。 |
関数 f(x) は(1,5)を通るので f’1)=5 -2+3a+b=5 3a+b=7…①
また、x=1において極大値をとるので、f’(1)=0 f’(1)=-6x2+6ax -6+6a=0…②
①、②より a=1, b=4 極小値4
問 次の関数が x=1 において極大値 4 をとるとき、a ,b の値と極小値を求めよ。
y=x3−6x2+ax+b
|
・x=1 のとき極大値 4 をとおる(1,4)のでf(1)=4がいえるので f(1)=4
f(1)=1-6+a+b = a+b-5=4 a+b-5=4 a+b=9 …②
・y’=3x2−12x+a x=1 のとき極大値 4 だから
f’ (x)=0 より
f'(1)=3x2−12x+a=3-12+a=0 a=9 …③
②と③よりa=9,b=0
y=x3−6x2+9x の極小値は y’=3x2−12x+9=3(x2−4x+3)=3(x−3)(x-1)
グラフイメージから x=3のとき極小値 y=27-54+27+0=0
問 一辺が12㎝の正方形の紙がある。いま、この四隅から1辺がx㎝の同じ大きさの正方形を切り取り、その残りを折り曲げて、ふたのない高さx㎝の直方体の箱を作る。
この箱の容量を最大にするにはxの値をいくらにすればよいか。 |
箱の底面の一辺 (12-2x)㎝ 、高さはx㎝だから、
箱の容量はx(12-2x)2= 144x-48x2+4x3=4x3-48x2+144x
箱の容量をyとおく y=4x3-48x2+144x
y'=12x2-96x+144= 12(x2-8x+12)=12(x-6)(x-2)
x=2.6 ただし0<x<6
| x |
0 |
|
2 |
|
6 |
| y' |
× |
+ |
0 |
- |
× |
| y |
× |
⤴ |
極大
128 |
⤵ |
× |
x=2cm
問 底面の半径と高さの和が12㎝の円柱がある。この円柱について、次の問いに答えよ。
x+h=12 高さ=12−x
(1) 底面の半径をx㎝とするとき、この円柱の高さをxで表せ。
(2) 円柱の体積をy㎤とするとき、yをxで表せ。
(3) 円柱の体積 y の最大値を求めよ。
|
答
(1) 底面の半径 x㎝+高さ=12cmより 高さ(12-x)㎝
(2) y = (12-x)πx2=12πx2-πx3=-πx3+12πx2
(3) y=-πx3+12πx2
y’=-3πx2+24π=-3πx(x-8)
x=0,8 (0<x<12) x=8のとき y=256π㎤
練習
母線の長さ5㎝,半径3㎝の直円錐の体積を求めてみよう |
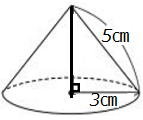 |
高さをhとおくと 三平方の定理から 9+h2=25 h2=25-9=16 h=4
よって、 V=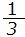 π×9×4=12π㎤
π×9×4=12π㎤
問
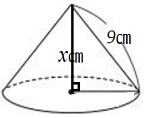
右図のような母線の長さ9㎝の直円錐の体積を最大にするには、高さをいくらにすればよいか。 |
 |
解説&答
半径をrとおくと 三平方の定理から x2+r2=81 r2=81-x2
体積をy㎤とおくと,y=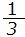 ×π(81-x2)×x ×π(81-x2)×x
=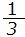 ×(81πx-πx3)=- ×(81πx-πx3)=-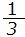 πx3+27πx πx3+27πx
y'=-πx2+27π=-π(x2-27) x=±3√3 右図より
x=3√3㎤ …答 |
 |
▲方程式、不等式への応用
方程式の解の個数
| 問3 関数 y = x3−6x2+aのグラフがx軸と異なる3点で交わるように、定数aの値の範囲を定めよ。 |
解答
x3−6x2+a = 0が異なる3つの実数解をもてばよい。つまり、
y=aとy=−x3+6x2が異なる3点で交わればよい
f(x)=−x3+6x2とおくと
f '(x)=−3x2+12x= −3x(x−4)
x=0で極小値f(0)=0
x=4で極大値f(4)=-64+96=32
y=aとy=f(x)のグラフを考えて 0<a<32
問4 関数 f(x)=x³−6x²+9x+1について、
定数kについて、方程式 f(x)−k = 0の異なる実数解の個数を求めよ。 |
解答
y=x³−6x²+9x+1
y’=3x²−12x+9 = 3(x−1)(x−3)
y’=0より x=1,3
増減表または、以下のような簡単なグラフを書いて求めよう。
y| ↗ ↘ ↗
1 3
x=1で極大値, x=3で極小値であることがわかる。
y(1)=5 極大値 y(3)=1 極小値
k>5, y=5 と1点で交わる 即ち1個
k=5 同じように考え 2個
1<k<5 3個 k=1 2個 k<1 1個
積分
■不定積分
x²+ C(定数) (微分すると) ⇒2x
F(x)+C f(x) |
以下の式のように表される。
 f(x)dx=F(x)+C (Cは定数)
f(x)dx=F(x)+C (Cは定数)
 は”積分”,または”インテグラル”と読む。また、定数Cを積分定数という
は”積分”,または”インテグラル”と読む。また、定数Cを積分定数という
| 2x (積分すると) ⇒x²+ C ※積分は微分の逆計算 |
▲不定積分の計算
(x)′=1 であるから  1dx= x+ C
1dx= x+ C
(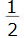 x²)′=x であるから
x²)′=x であるから  x dx=
x dx= 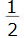 x²+ C
x²+ C
(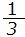 x3)′=x² であるから
x3)′=x² であるから  x² dx=
x² dx= 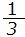 x3+ C
x3+ C
でよって、次の公式が成り立つ
一般に、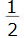 x²+ C (Cは任意の定数)で表される関数は、xsplaystyle x}の原始関数である。
x²+ C (Cは任意の定数)で表される関数は、xsplaystyle x}の原始関数である。
上の式からxの原始関数は一つだけではなく、無数にあることがわかる。
a=0,1,2のとき
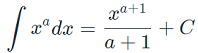 公式 公式  1dx=は 1dx=は dx=と書くことが多い dx=と書くことが多い |
不定積分の公式
 k f(x) dx = k k f(x) dx = k f(x) dx (kは定数) f(x) dx (kは定数)
 {f(x)+ g(x)} dx = {f(x)+ g(x)} dx = f(x) dx+ f(x) dx+  g(x) dx g(x) dx
 {f(x)- g(x)} dx = {f(x)- g(x)} dx = f(x) dx- f(x) dx-  g(x) dx g(x) dx |
問1 以下の関数の不定積分を求めなさい。
① 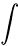 x dx ② x dx ② 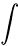 3x2 dx ③ 3x2 dx ③ 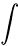 dx ④ dx ④ 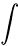 5x4 dx 5x4 dx
⑤ 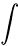 x²dx ⑥ x²dx ⑥ 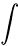 6x dx ⑦ 6x dx ⑦ 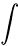 (-8x) dx ⑧ (-8x) dx ⑧ 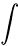 (-4x2) dx (-4x2) dx |
答 ①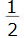 x2 +C ③x+C ④
x2 +C ③x+C ④
問2 以下の関数の不定積分を求めなさい。
① 5x2 dx ② 5x2 dx ②  (3x2-6x+2) dx ③ (3x2-6x+2) dx ③  (3x-1)(x+1) dx (3x-1)(x+1) dx |
① ② x3-3x2+2x+C ③ x3+x2-x+C
問3 次の条件を満たす関数F(x)を求めなさい。
F'(x)=3x2-4x+2, F(1)=5 |
微分した F'(x)=3x2-4x+2を積分してみよう。
F(x)= (3x2-4x+2) dx = x3-2x2+2x+C
(3x2-4x+2) dx = x3-2x2+2x+C
ここでF(1)=5 であるから、F(1)=1-2+2+C= C+1=5 よってC=4
x3-2x2+2x+4…答
■定積分
関数f(x)の不定積分の1つをF(x)とするとき F(x)をf(x)の原始関数とすると
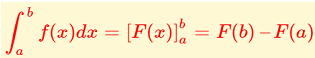
この定積分を求めることを「f(x)をaからbまで積分する」といいます。
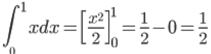
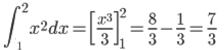
問 ①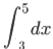 ② ②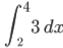
|
答 ①2 ②6
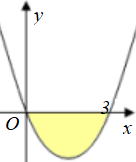
放物線y=x2-3xとx軸で囲まれた面積が定積分で簡単に求められるのでやってみましょう。
y=x(x-3)とx軸で囲まれた個所は右図のようになります。
y=x2-3xを0から3まで積分します。
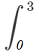 x2-3xdx= x2-3xdx= 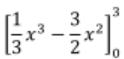 = - = -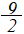
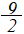 が答になります。どうしてマイナスがついたのでしょう? が答になります。どうしてマイナスがついたのでしょう?
原因は積分区間において、f(x)≦0なのに、そのまま積分したからです。 |
 |
また円を例にとると、半径r、円のまわりの長さ(円周:2πr)を半径で積分すると円の面積になります。
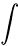 2πr dr=πr2
2πr dr=πr2
反対に円の面積を半径で微分すると円周になることが分かります。
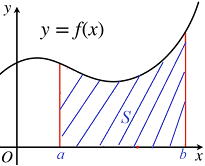
区間 a≦x≦bにおいて、f(x)≧0のとき、
曲線 y=f(x)とx軸, x=a, x=bで囲まれた図形の面積Sは
S=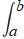 f(x) dx f(x) dx
|
 |
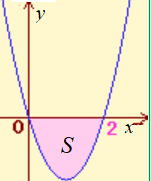
問 放物線 x2−2xとx軸で囲まれた面積を求めなさい。
y=x2−2xとおく。y=x(x−2) (右図) y<0
S=-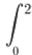 x2−2x dx =4/3 x2−2x dx =4/3
4/3…答 |
 |
| 問 放物線 y=3x2+6x-9とx軸で囲まれた図形の面積Sを求めなさい。 |
左辺=3x2+6x-9=3(x2+2x-3)=3(x-1)(x+3)
-3≦x≦1 では y≦0であるから、求める面積Sは
3x2+6x-9を-3から1まで定積分すると 32…答
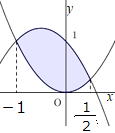
| 問 2つの放物線 y=x2と y=-x2-x+1で囲まれた部分の面積Sを求めなさい。 |
解答 囲まれている部分ではグラフ y=-x2-x+1の方が上になっています。
y=x2と y=-x2-x+1の交点は x2=-x2-x+1
2x2+x-1=0より -1と 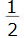 (左図) (左図)
(-x2-x+1)−x2=-2x2-x+1
s=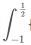 {(-2x2-x+1)}dx {(-2x2-x+1)}dx
これを計算すると 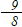 …答 …答 |
 |
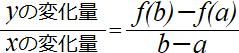 を、xの値がaからbまで変化するときの平均変化率という。
を、xの値がaからbまで変化するときの平均変化率という。

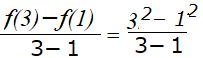 =4
=4
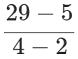 =12…答
=12…答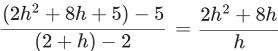 =2h+8…答
=2h+8…答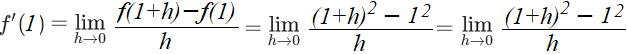
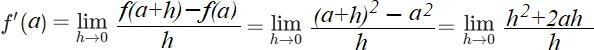
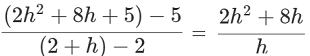 =2h+8
=2h+8
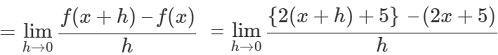
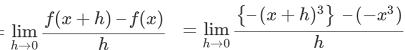


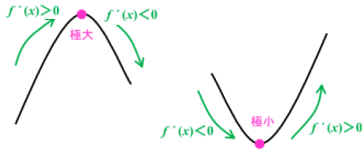









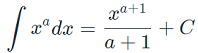 公式
公式 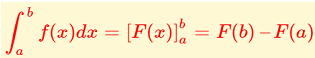
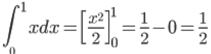
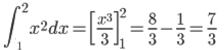
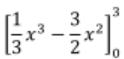 = -
= -


