![]()
三角比も建築、土木、化学、測量、通信(音声デジタル変換)等、多くの分野で使われています。
 |
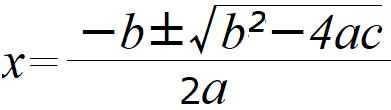 |
|
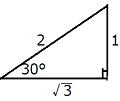
問 次の値を求めなさい。 |
上の問題解答をよく見てください。
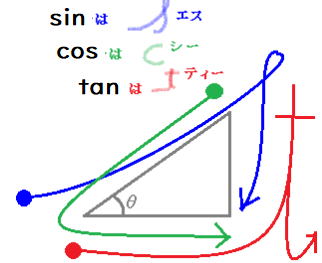
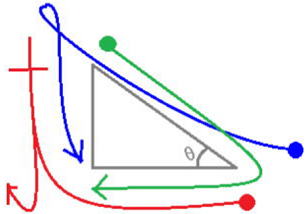
sinA=cosB cosA=sinB tanAは逆数になることがわかります。
つまり sin(90°-A) = cosA になります。同様に、
cos(90°−A) = sinA (90°−A) は角度Bですから
 0°≦θ≦90°の範囲で
0°≦θ≦90°の範囲で
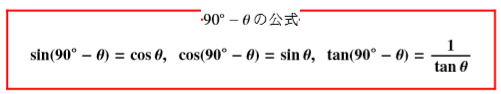
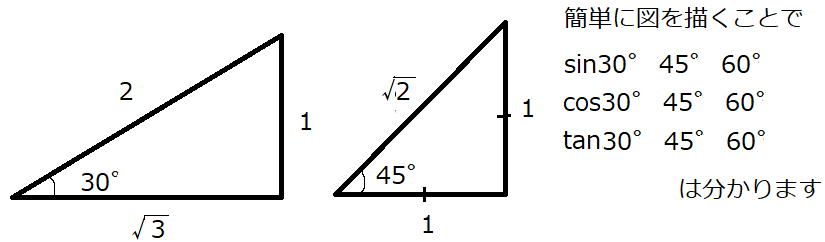
以下の表の穴埋めは、中間や期末テストに必ず出題されます。覚えておくように指導する学校がありますが、
覚えるのは大変だ。それにテストが終わってしばらくすると忘れている。
できたら、自分で考えてほしい。 表の下に考え方を説明しよう。
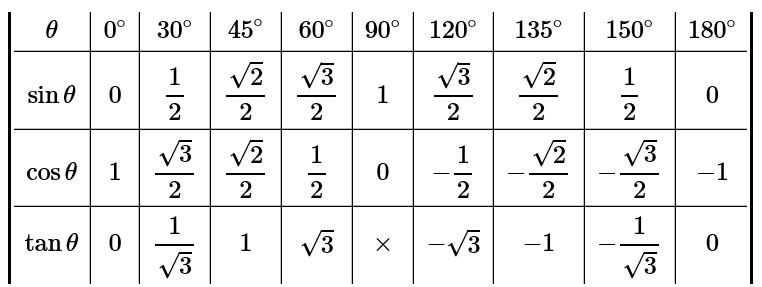
それでは以下の残りの角度は?
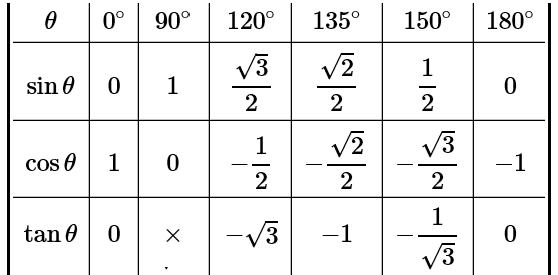
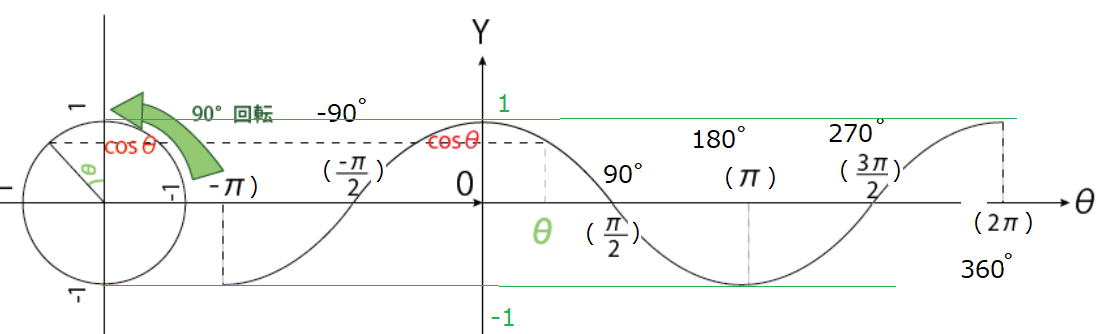
グラフで考えてみましょう。
グラフは2年で学習しますが、これはいま覚えていたほうがbetterだと思います。
y = sinθのグラフ (θは角度)
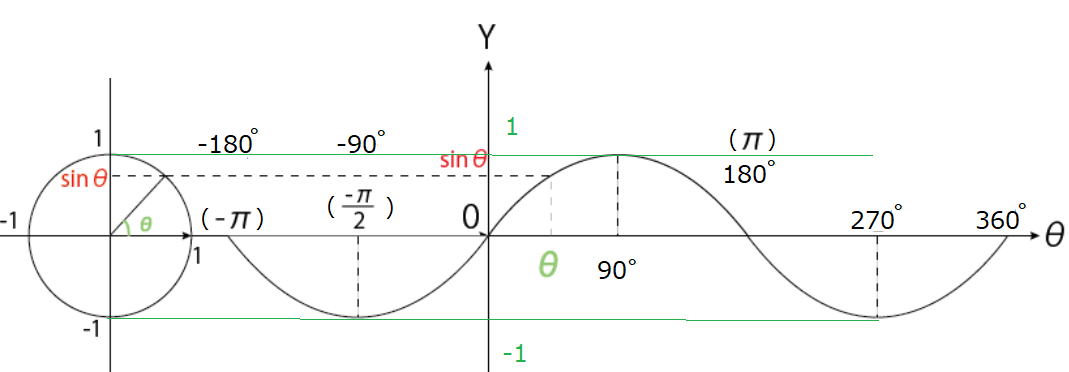
y = cosθのグラフ (θは角度)
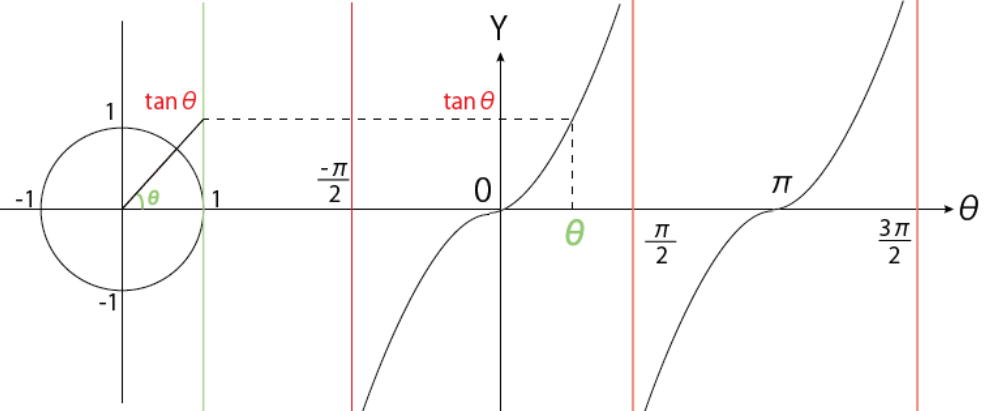
tanθグラフは参考まで
 |

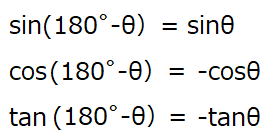
それでは以下の問題をやってみましょう。
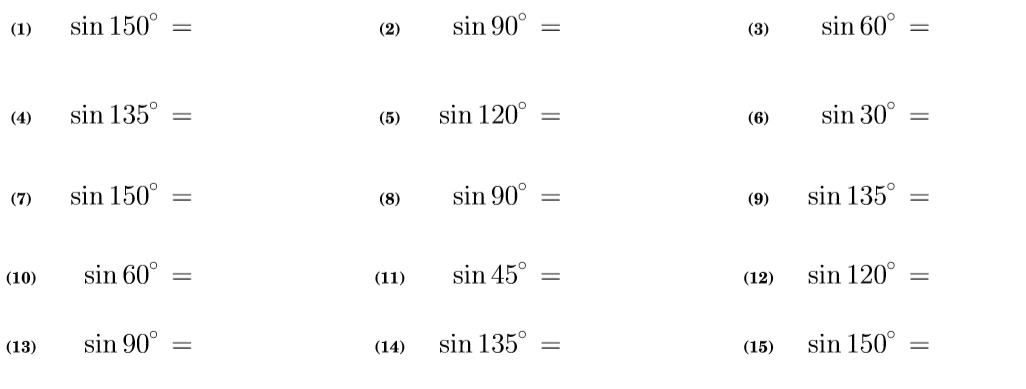
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
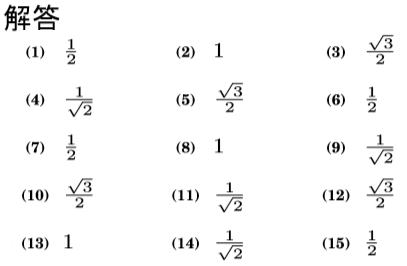
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
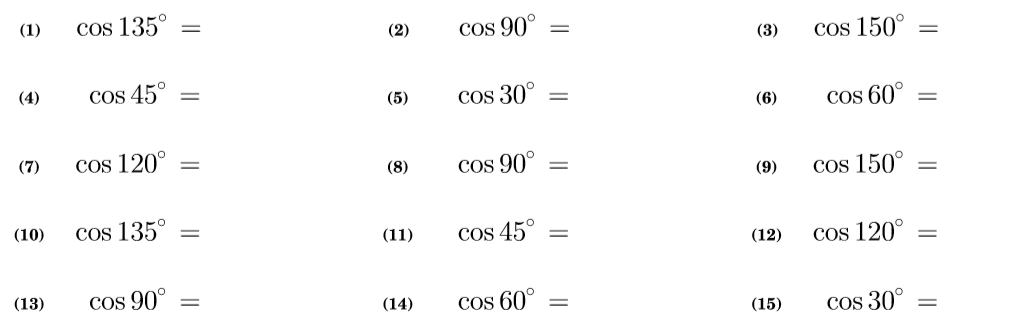
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー-------
解答
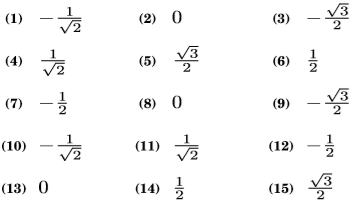
-----------------
![]() 以下は大切な公式。しっかり覚えておこう。
以下は大切な公式。しっかり覚えておこう。
| sin2θ+cos2θ=1 ……公式① tanθ= |
| sinθ= sin2θ= |
 |
|
問1 0°≦θ≦180°とする。 |
![]() より
より
sin2θ=1−cos2θ sin2θ=1−![]() =
=![]()
sinθ=±![]()
0°≦θ≦180°なので sinθ=![]() …答
…答
|
問2 0°≦θ≦180°とする。 |
![]() より
より
sin2θ=1−![]() sinθ=±
sinθ=±![]()
0°≦θ≦180°なので sinθ= ![]() …答
…答
公式 tanθ=![]() より
より ![]() ÷
÷![]() =1 …答
=1 …答
| 問3 0°≦θ≦180°とする。 cosθ= |
解説 sinθtanθ=sinθ×![]() =
= 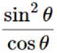
![]() cosθ=
cosθ= ![]() を代入
を代入
sin2θ=1−![]() =
=![]() sinθtanθ=
sinθtanθ= 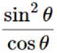 だから
だから
sinθtanθ=![]() ÷
÷![]() =
= ![]() …答
…答
| 問4 0°≦θ≦180°とする。 sinθ=
|
| 問5 角度Aが鋭角で、cosθ= |
![]() より
より
sin2θ=1−cos2θ=1−(![]() )
)
sinθ= ±![]() Aは鋭角だからsinθ=
Aは鋭角だからsinθ= ![]() …答
…答
tanθ=![]() より tanθ=
より tanθ=![]() ÷
÷![]() =
=![]() …答
…答
■正弦定理
![]()
![]() =
=![]() =
=![]()
上の公式は必ず覚えよう。以下に一例をとって説明します。
![]()
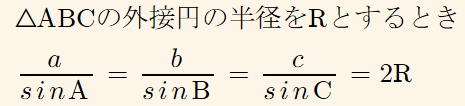 が成り立ちます。
が成り立ちます。
以下、証明してみよう
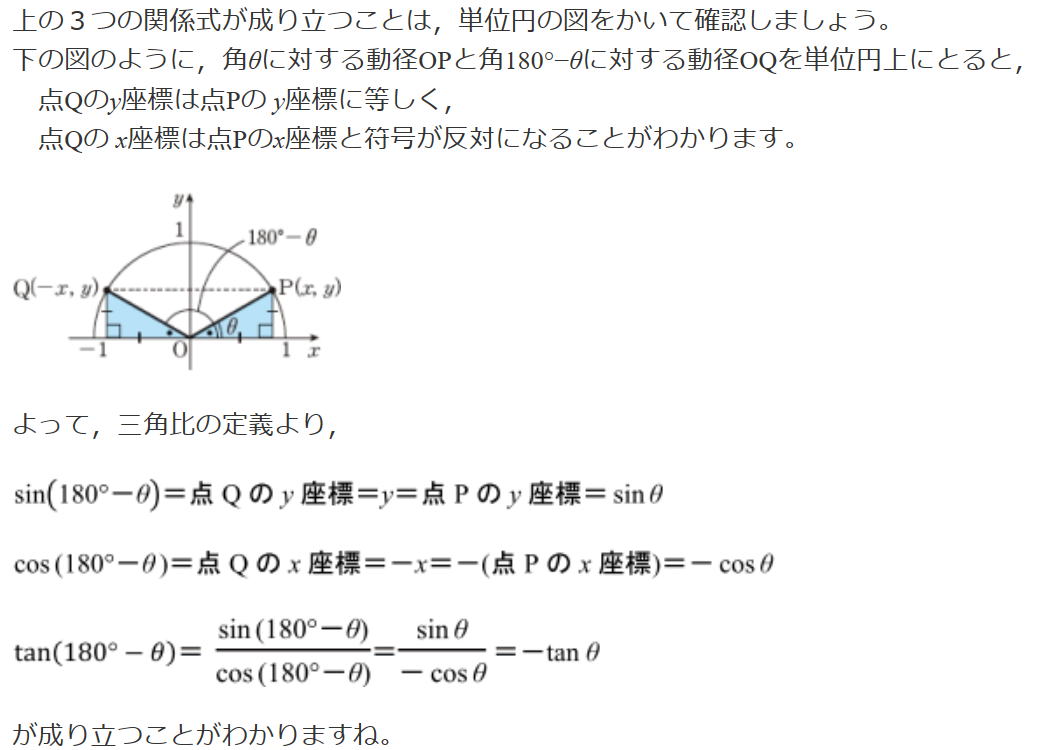
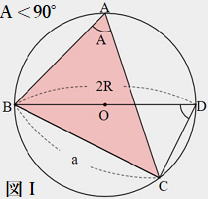
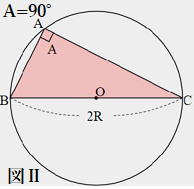
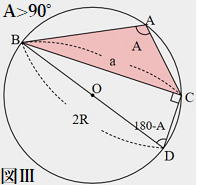
| 証明 Ⅰ A<90°のとき(図Ⅰ) Bを通る直径をBDとする。直径の円周角は90°なので∠DCB=90° 等しい弧に対する円周角は等しいので∠BDC=A a=2Rsin∠BDC=2RsinA よって Ⅱ A=90°のとき(図Ⅱ) a=2R,sin90°=1より a=2R=2Rsin90°=2RsinA よって Ⅲ A>90°のとき(図Ⅲ) したがって |
   |
| 問1 三角形ABCにおいて、AB=4、A=75°、B=60°のとき辺ACの長さ、および外接円の半径を求めなさい。 |
| 解説 まず、以下のような図を簡単に書いてみよう。 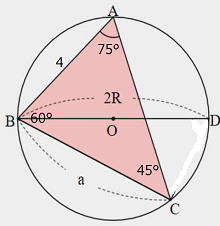 |
公式から ACの長さ=b で, まずACの長さを求めましょう。AC=b bsin45°=4sin60°(sin45=1/√2, sin60°=√3/2) 次に半径Rを求める。 外接円の半径は 2R=4/sin45° R= 2/sin45°= 2√2 答 |
| 問 a=6,A=30°,B=45°のとき,外接円の半径Rとbを求めなさい。 解答 簡単に絵を描いてみよう。 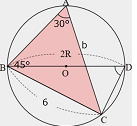 |
答
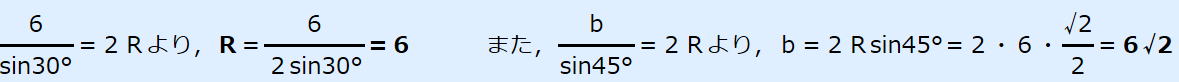
余弦定理
![]()

| 問1 ① 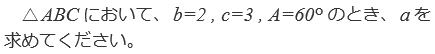 問2 ② 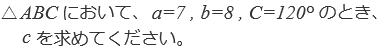 |
簡単な図を書きましょう。
正弦定理を使おうとしても、aの値が未知なので、ここは余弦定理を用います。

問3 問4 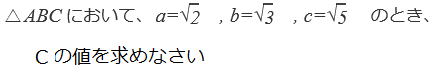 |
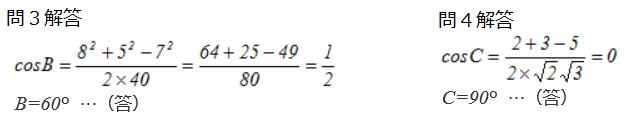
円の接線と弦の作る角
円の弦と、その弦の一端を通る接線のつくる角は、その角の内部にある弧の円周角と等しい(接弦定理)
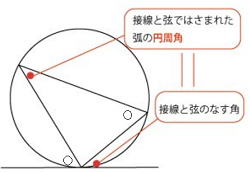
問 ∠x の大きさを求めよ。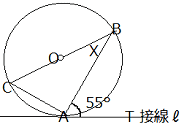 |
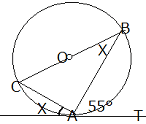
答
∠x =180°- (90°+ 55°) =35°
方べきの定理
| 円の2つの弦AB,CDの交点(図1)、 または、それらの延長の交点(図2)をPとすると、 PA×PB=PC×PDが成り立つ。 図1 図2 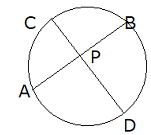 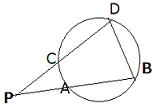 このことは円と直線の交点に作られる2組の三角形が、それぞれ相似であることから証明できます。 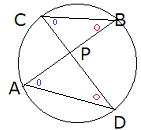 図1 どちらも弧AC、BDの円周角で∠A=∠C、∠B=∠Dから相似 図1 どちらも弧AC、BDの円周角で∠A=∠C、∠B=∠Dから相似 |
問1 下の図において、PAの値を求めよ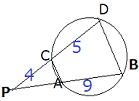 PC=4, CD=5,AB=9 PC=4, CD=5,AB=9 |
PA = x とおく。
方べきの定理より、4・(4+5)=x・(x+9)より、
x2 + 9x = 36 x2 + 9x ⊸ 36 = 0
乗法の公式より、(x ー 3)(x +12)
x>0だから x = 3 ・・・答
検証してみよう AP=3なら
3・(3+9)=36 4・(4+5)=36 でOK!
問2 下の図において、xの値を求めよ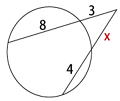 |
方べきの定理より、3・(3+8)=x ・(x +4)より、
x 2 + 4x − 33 = 0
解の公式より、x >0だから x = -2 + √37・・・答
三角形の面積を求める
△ABCの2組の辺とその間の角度が分かれば
三角形の面積が求められます。
公式は1つ覚えれば十分です
![]()
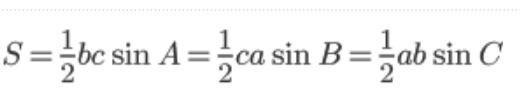
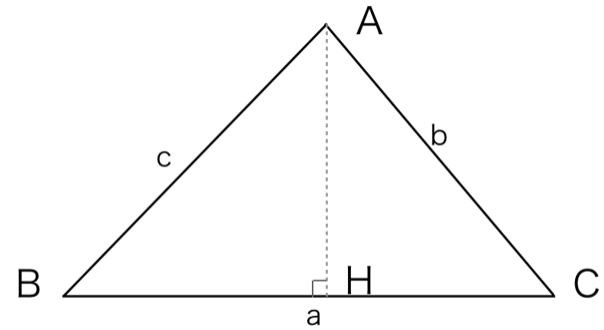
証明 角度Bが分かっているときを例にとります。

ツール:
![]()
![]()
![]()